Минимальное остовное дерево

? такую задачу при помощью связанного ориентированного графа.

Для каждого ребра будет задан вес w(u,v) определяющей стоимость соединения u с v. Мы хотим найти ациклическое подмножество ребер T<=E которое соединяет все вершины и чей общий вес минимален W(T)=Ew(u,v)-> min (u,v) э T

Часто для графа такое дерево бывает не единственным т.е. заменив некоторые соединение на другое с таким же весом снова получим каркас. Будем рассматривать алгоритм Прима и алгоритм , КрусКал

Оба алгоритма являются жадными. Общую схемы согласно которой минимальное основное дерево растет путем добавления к нему ребер по одному. На каждом шаге алгоритма определяем ребро uv которое можно добавить к подмножеству минимального основного дерева A.

A U {(u,v)} тоже подмножество минимального остовного дерева. Такое ребро называется безопасным.

MinOstTree(G,w)

1. A=0

2. While A не является остовным деревом

3. Do beign найти безопасное ребро (u,v)

4. A=A U {(u,v)} end

5. Return A

Как найти безопасное ребро

Разрез (S,(V-S)) неориентированного графа G=(V,E) называется разбиение v представленным следующем образом.

Говорим что ребро пересекает разрез S,(V-S) если одна из вершин содержит S а другая v-s. Разрез согласован с множеством А по ребрам, если не одно ребра из А не пересекает разрез. Ребро пересекающее разрез является легким, если оно имеет минимальный вес среди всех ребер пересекающих S.

Правило для распознавания безопасный ребер дает следующая теорема. Пусть G=(V,E) связанный неориентированный граф с действительной функцией w определена на E. Пусть А подмножество Е которая входит к некоторое минимальное основное дерево j. (S,(V-S)) разрез j согласованный с А по ребрам, а (u,v) легкое ребро пересекающее этот разрез, тогда ребро(u,v) является безопасным для А

Алгоритм прима построения минимального каркаса. В алгоритме прима каркаса А образует единое дерево. В это множества А добавляются ребра, которые являются ребра минимального веса, соединяющее ? дерева с вершиной дерева.

Ребра имеют вес ? графом описываем ???

A:array [1..N,1..N] of integer; Q=(V,T) , T<=E

Для реализации метода используется 2 множества. SM,SP:set of [1..N]; Сначала множество SM содержит все вершины графа, а SP пустое. SP=[]; SM:=SM+[i]; Если ребро (I,j) включается в T, то один из номеров вершин I и j исключается из SM но добавляется в SP. В первом шаге обе номера должны войти в SP.

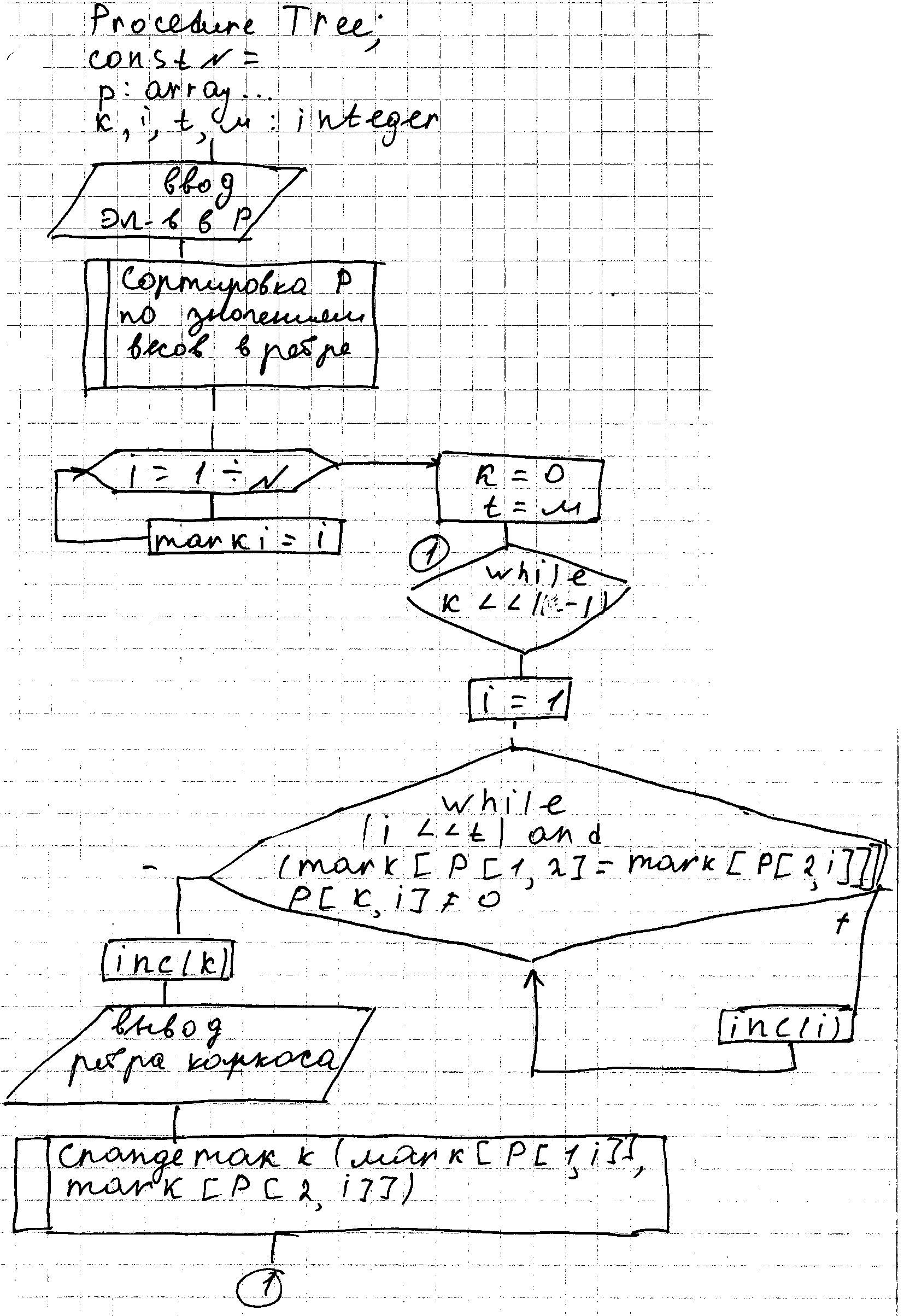
Блох схема алгоритма прима

Procedure Tree; var SM, SP: set of [1..N];

Min,I,j,l,k,t:integer;

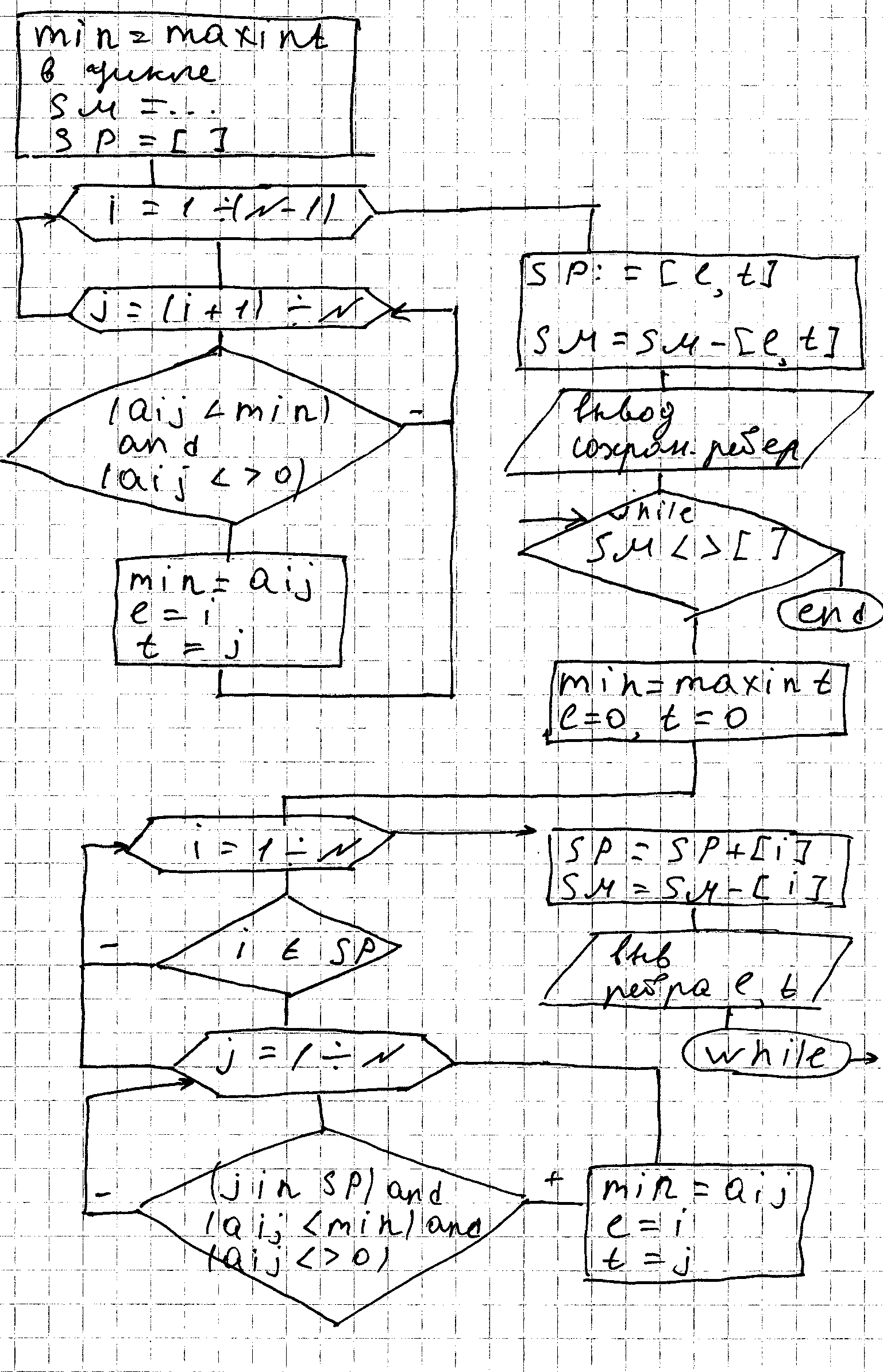
Метод КрусКала

В алгоритме крускала является лесом. А – множество всех вершин. В А добавляются безопасные ребра которые являются ребрами минимального веса, объединяющие 2 различных компонента.

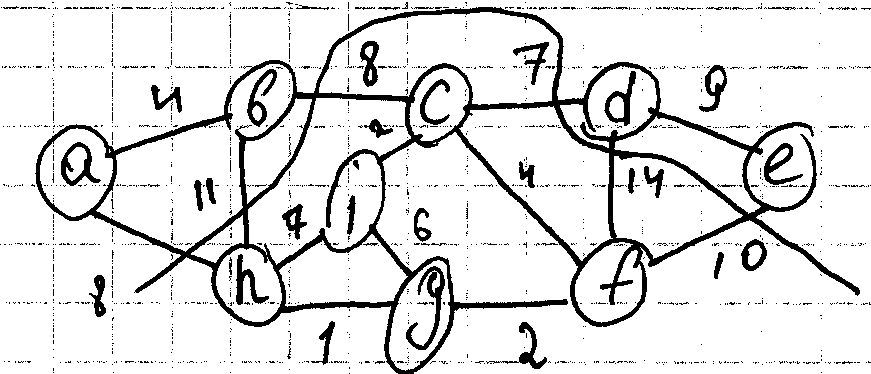
Пр. Дан граф, построить

1. Начать с графа Q ? и не имеет ребер

2. Упорядочить ребра графа j в порядке не убывания их весов.

3. Начав с первого ребра в этом перечне добавлять ребра в граф q соблюдая следующее условие: добавление не должно приходить к появлению циклов Q.

4. Повторять шаг 3 до тех пор, пока число ребер в Q не станет равным n-1

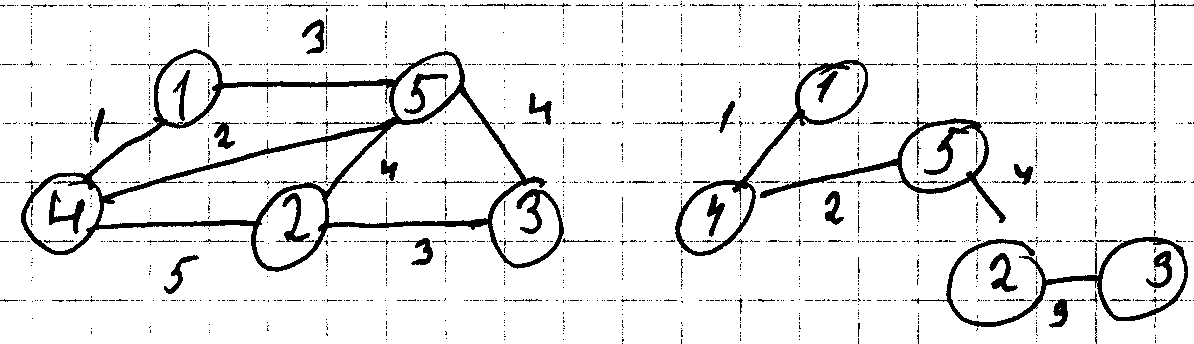
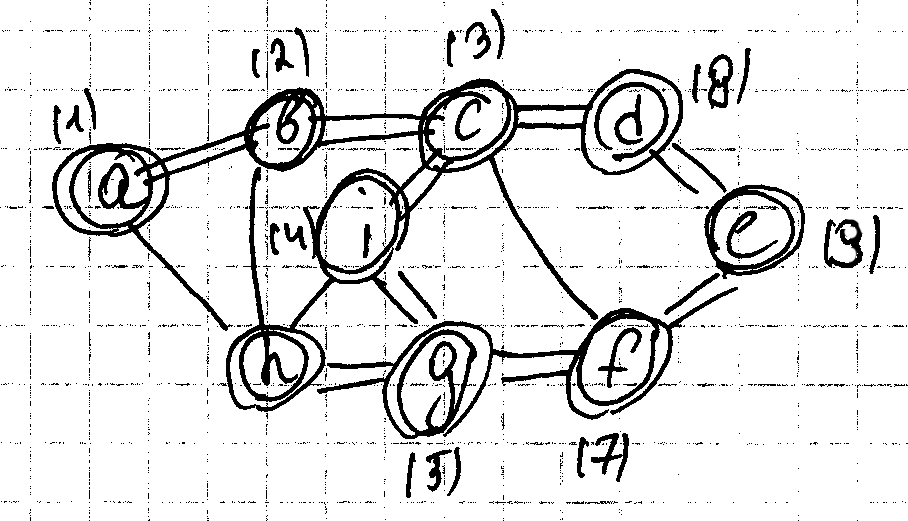
Получившиеся дерево будет каркасом минимального веса.

Для реализации 3-го шага в программу вводят массив меток вершин графа.

Mark:array[1..n] of integer; Начальное значение mark=номер вершин: Mark[i]:=I

Ребро выбирается в каркас, если вершины, соединенные им, имею разные значения меток. Тут циклы не образуются.

Процесс изменения значений

Num	ребро	Массив меток
0	-	(1,2,3,4,5)
1	(1,4)	(1,2,3,1,5)
2	(4,5)	(1,2,3,1,1)
3	(2,3)	(1,2,2,1,1)
4	(2,5)	(1,1,1,1,1)

Граф опишем перечислением ребер с указателем их веса с помощью массива.

P:array[1..3,1..n*(n-1)div2] of integer

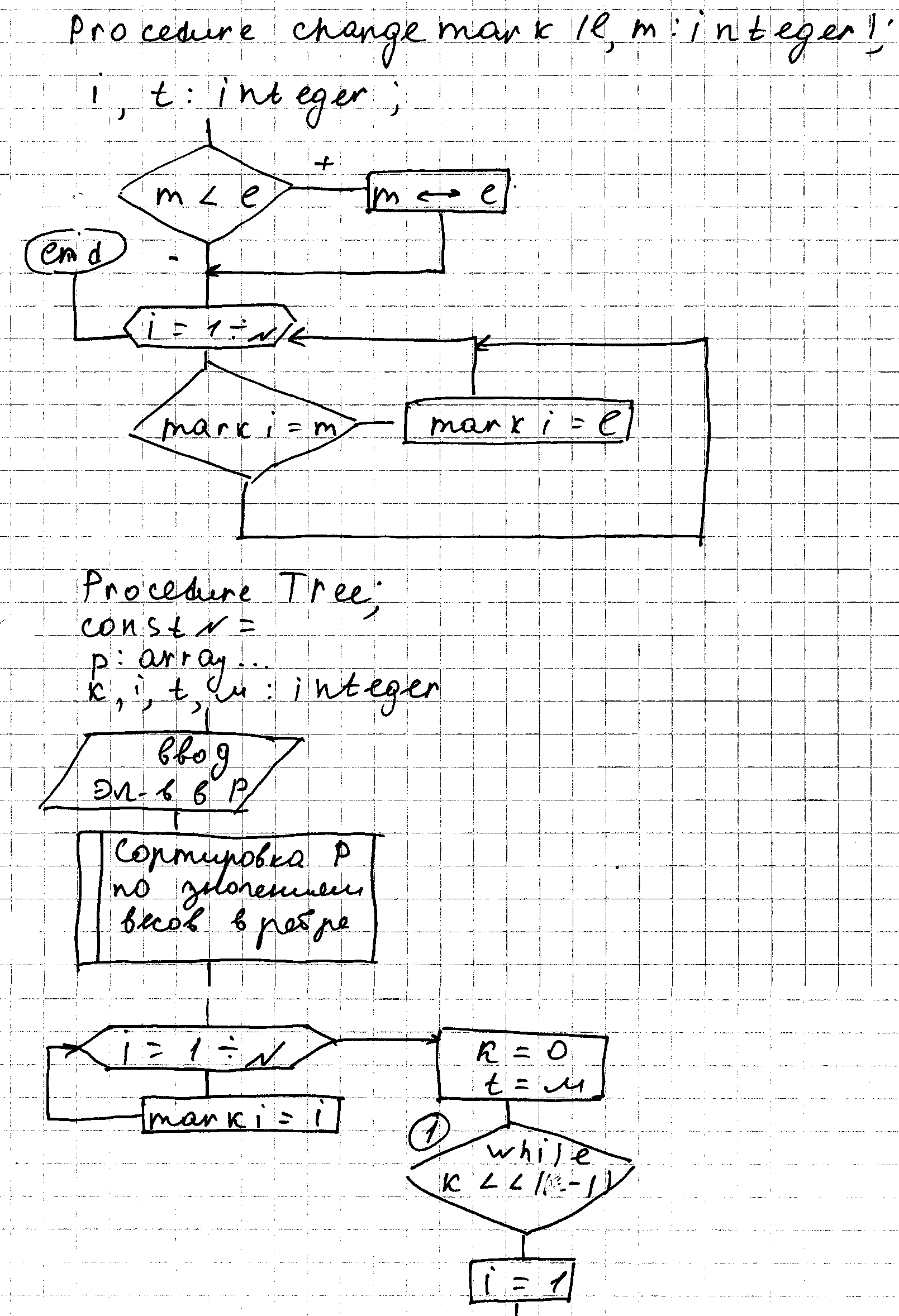
Для алгоритма нужна процедура изменения элемента mark[i], массив mark – глобальный:

Procedure change_mark(l,m:integer);