Эйлоровый цикл

Проходит 1 раз по каждому ребру Теорема: Связный, не ориентированный граф G, содержит цикл, когда число вершит нечетной степени =0. Если цикл существует, значит что следуя вдоль цикла можно нарисовать граф на бумаге не открывая карандаша.

Алгоритм поиска Дано: граф G удовлетворяющий теореме.

Решение: Используем прямой отрезок графа методом поиска в глубину. Притом ребра удаляются. Порядок просмотра (номера вершин) запоминаются. При обнаружении вершин, из которых ее номер записывается в стеке и просмотр идет от предыдущей вершины. Обнаружение ребр с 0-ой вершины говорит, что найден цикл. Его можно удалить (четность не изменяется) продоржает процесс поиска. В результате в стеке – номера вершины графов в порядке совпадает Эйлорову циклу.

Гомельтоновый цикл

Граф Гомельтоновый, если в нем есть цикл, содержащий каждую вершину графа. Не все графы Гомельотовы

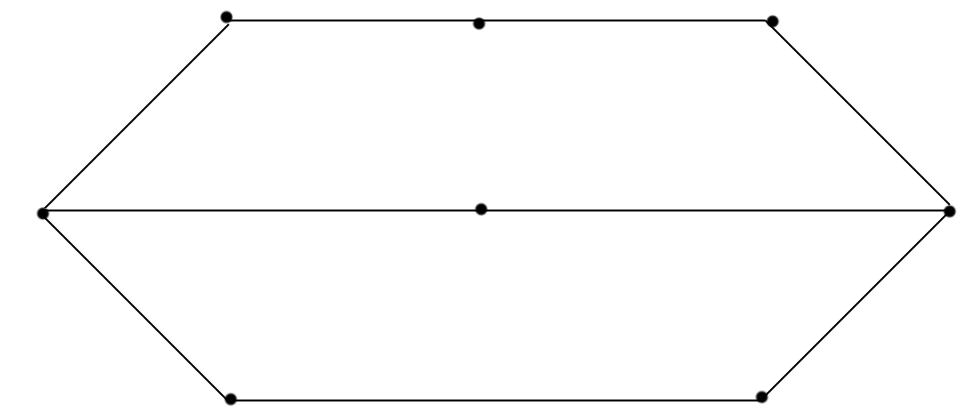
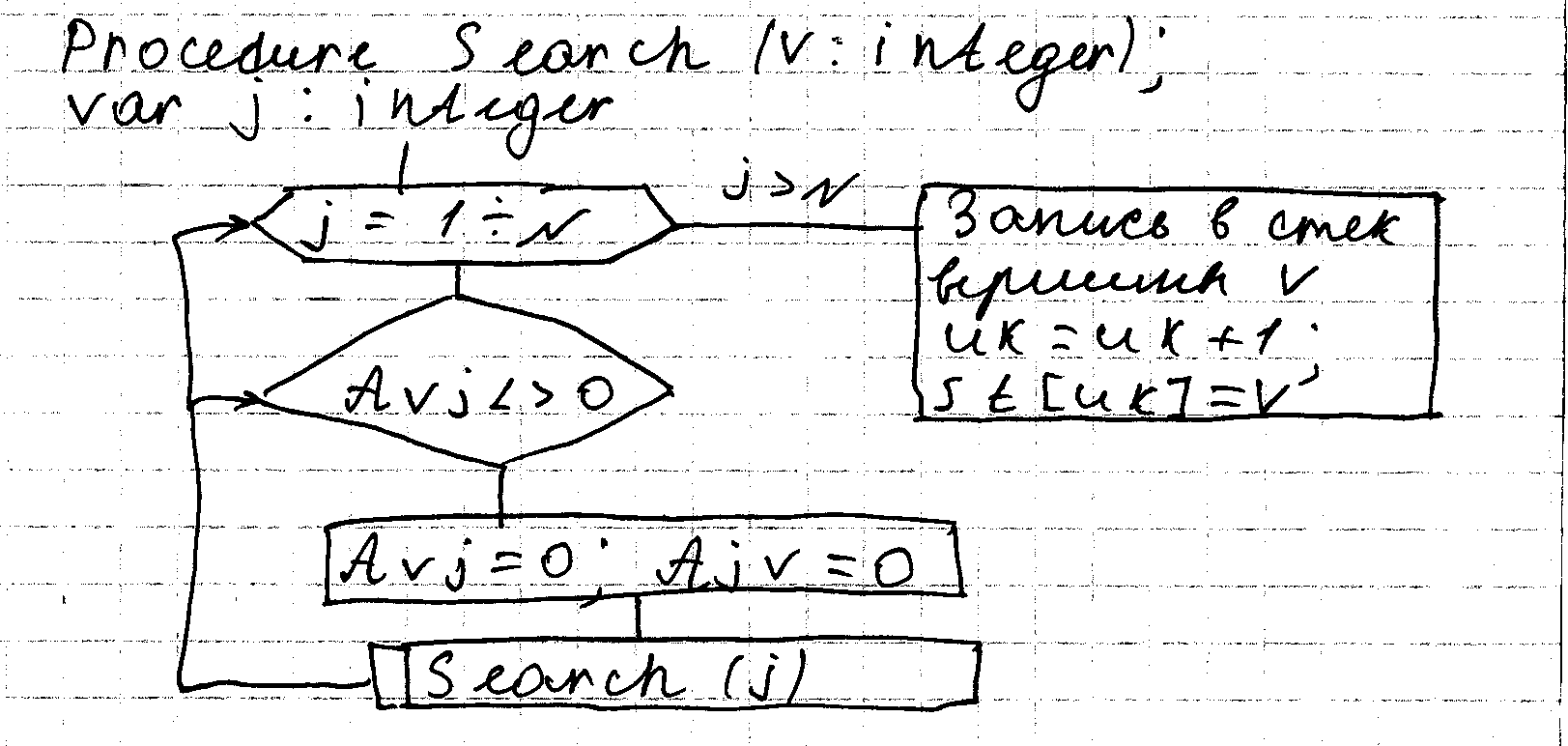
Связанный не ориентированный граф дан. Найти Гомельтоновый цикл, если есть решение использующее перебор с возратом.

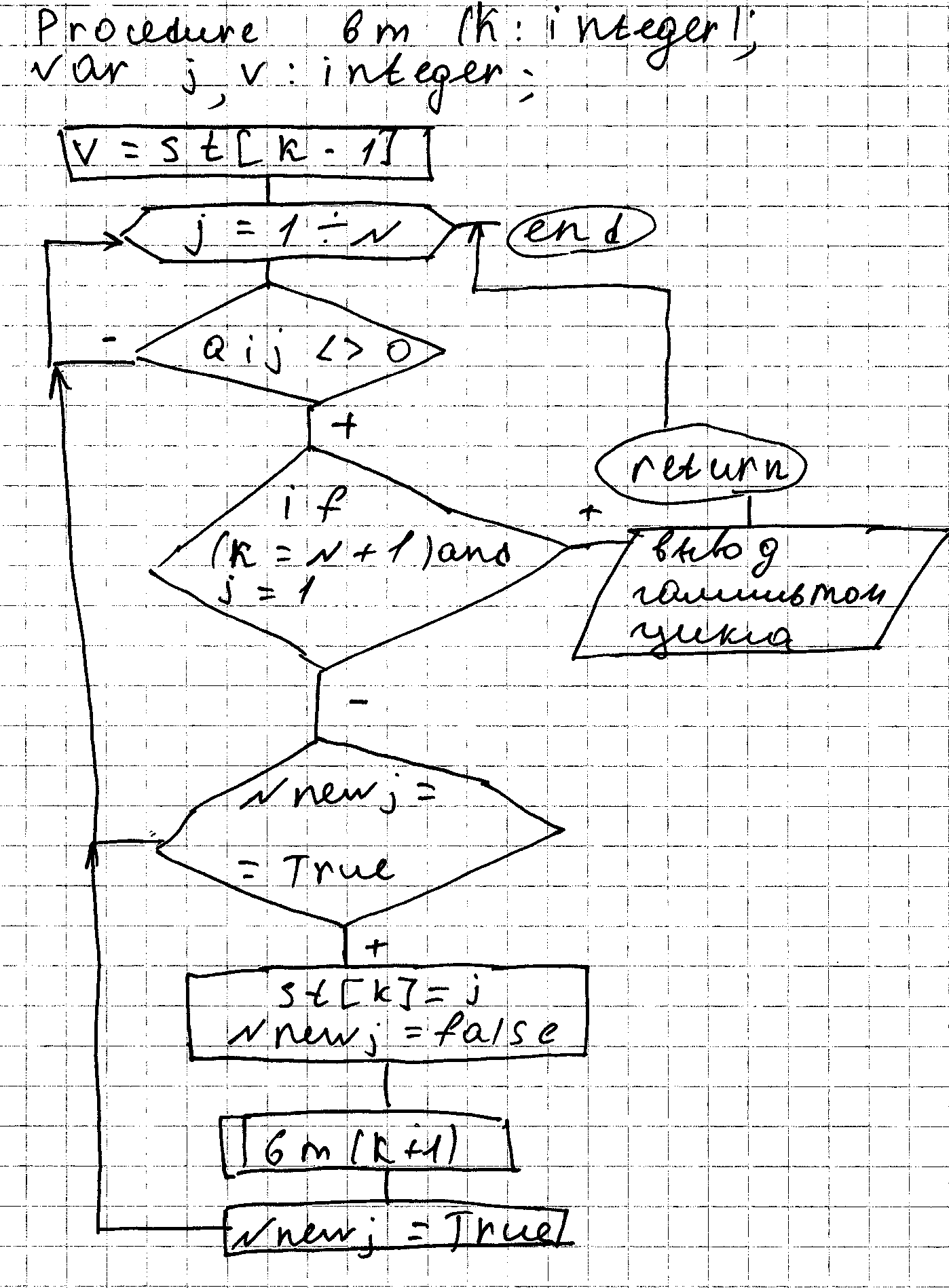
Начнем поиск решения на примере p с первой вершиной графа. Пусть найдены k – компонент решения. Рассматриваем ребра входящие из последней вершины. Если такие есть, что идут в ранее не просмотренной вершины, то включаем первую вершину в вершину и помечает ее как просмотренную. Получено k+1 комп?онент решение. Если вершины нет, то возврат к предыдущей вершине, и пытаемся найти ребро из вершины выходящее из нее. Решение получено, если ? и получим возможность достижения у последней к первой вершине. Решение выводится, продолжается процесс ? следующий цикл.

Кротчайшие пути в ориентированных графах.

Дано ориентированный граф G с набором вершин и ребер (G=(V,E)), граф взвешенный, ? коэффициенты на дугах Aij; ij=1 to n где n- число вершин; S – начальная вершина; Z – конечная вершина; путь между s и z оценивается ΣAij (ij принадлежит пути s->t). Хотели получить путь с минимальной оценкой.

Задача разбирается на 2 подзадачи - Сам путь -значение минимума веса

Обозначим min веса через D[s,t]

На сегодня неизвестны алгоритмы, определяющие один D[s,t] все алгоритмы определяют вес? Б до всех вершин графа.

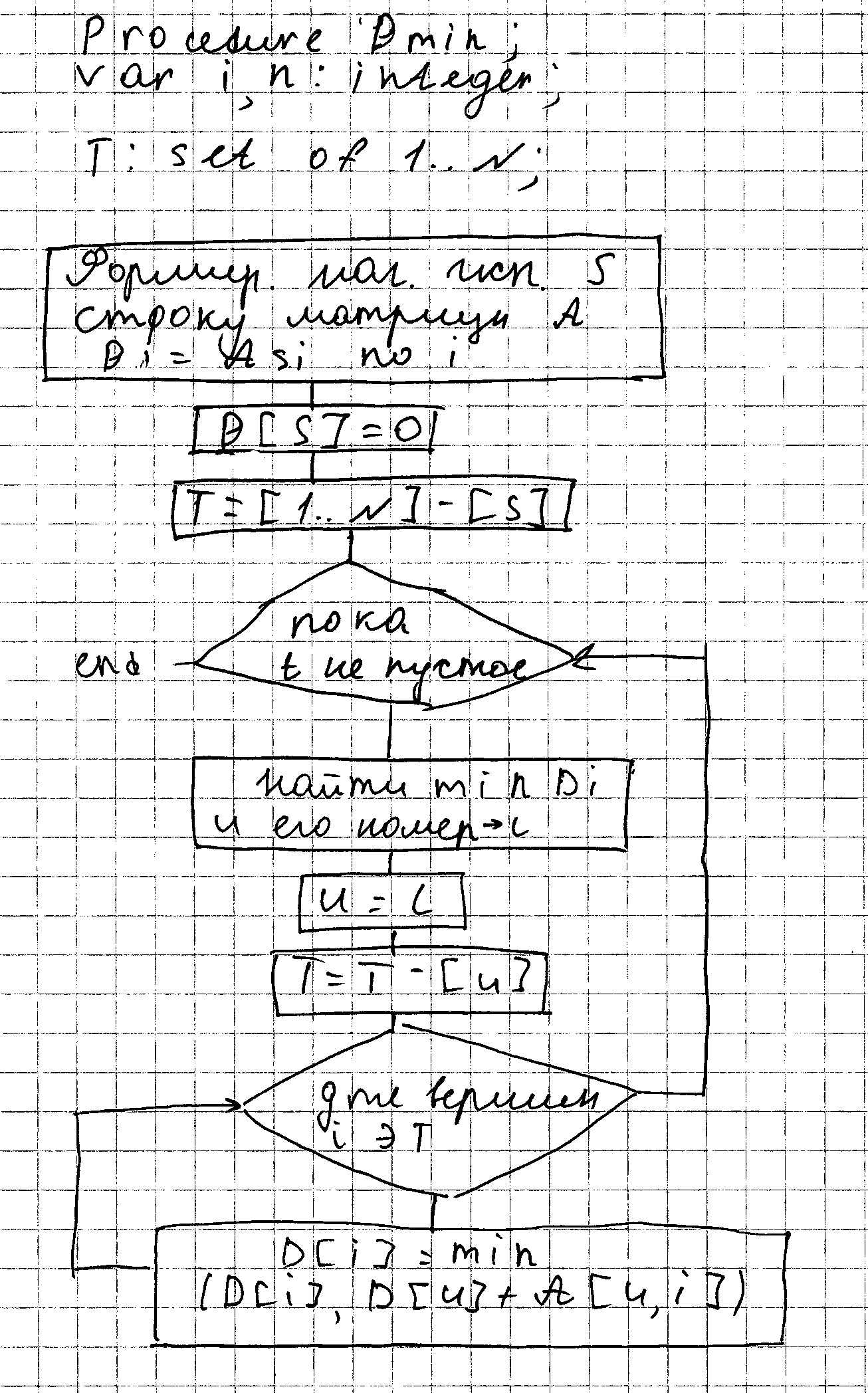
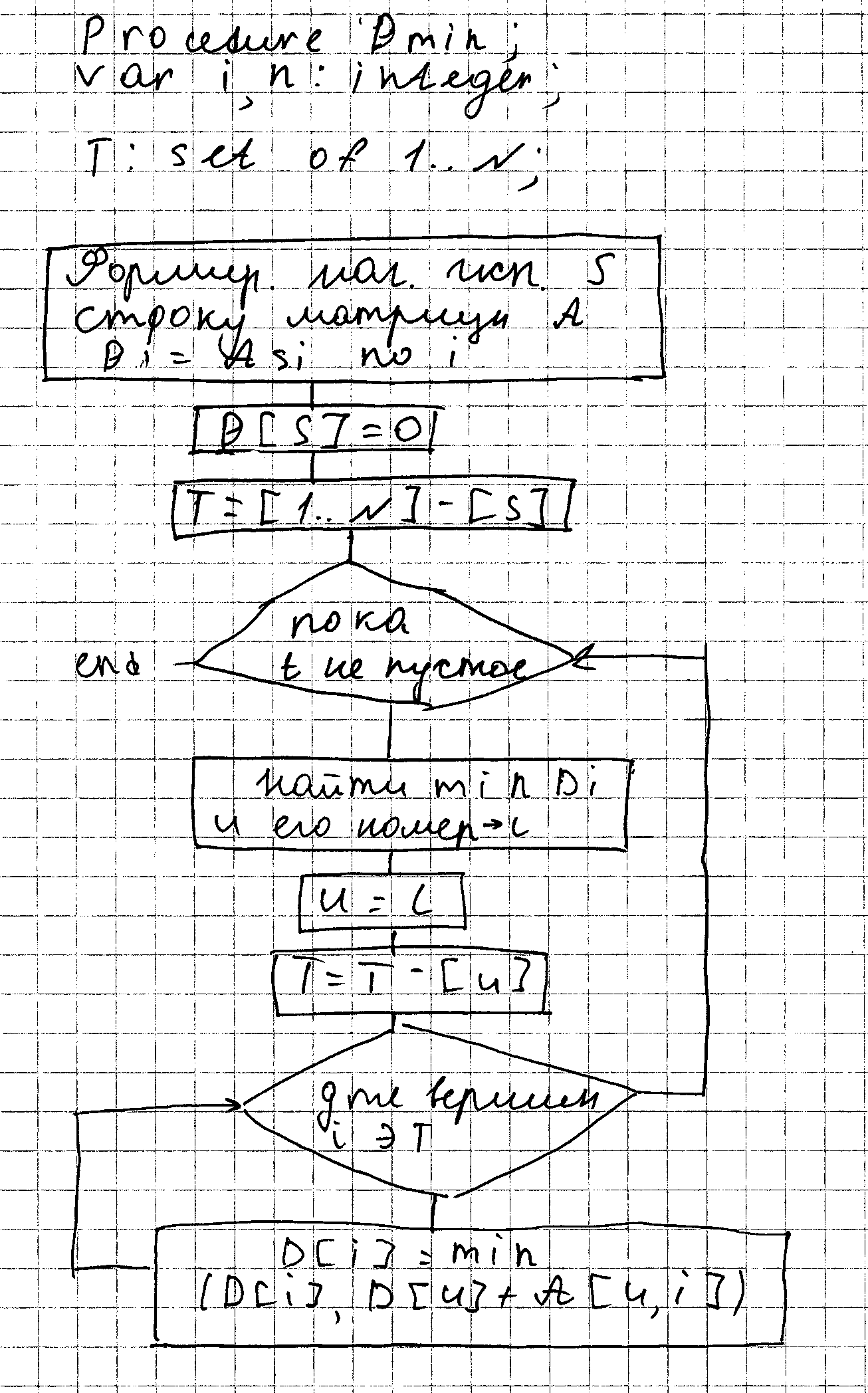
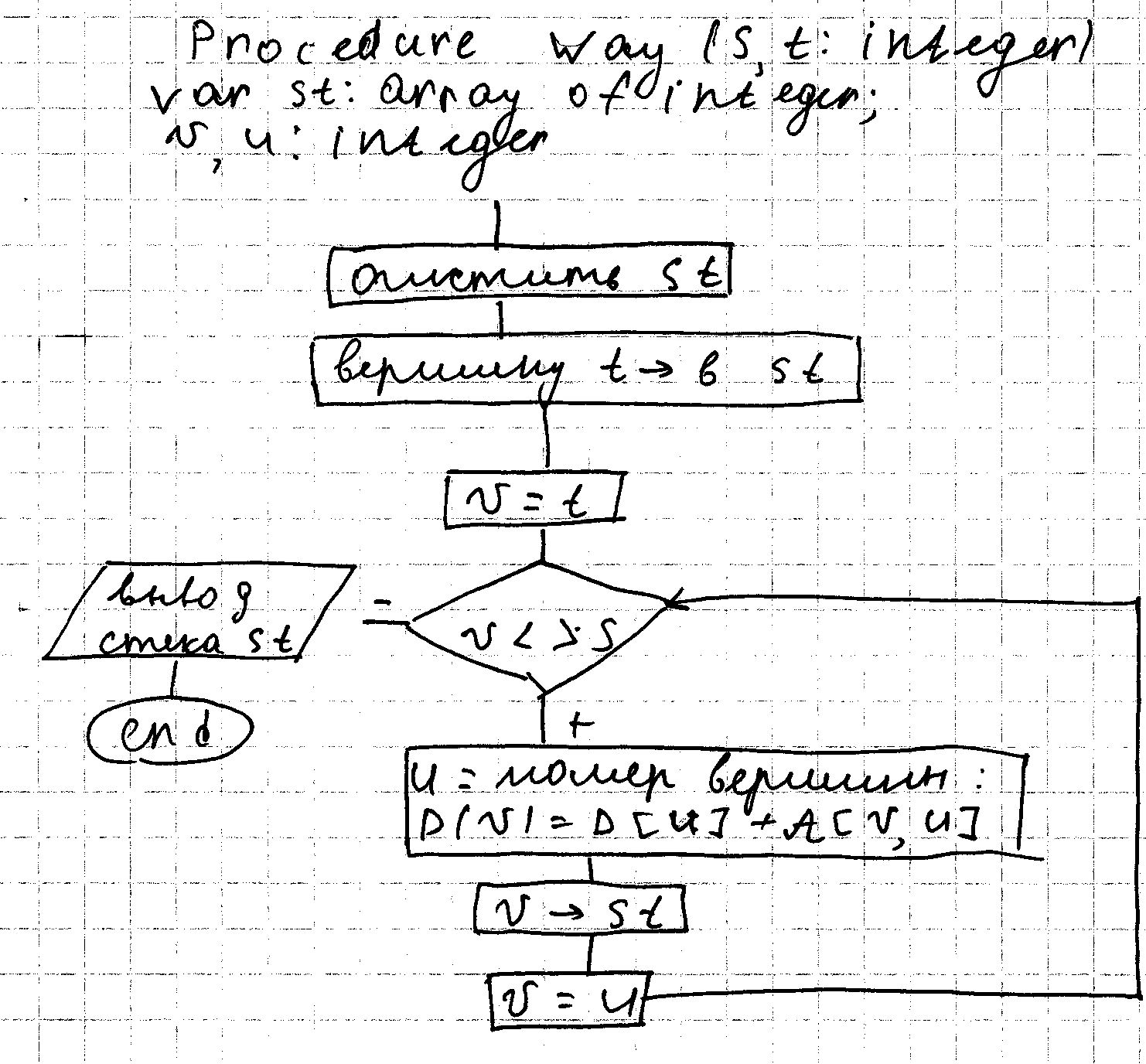
Предположим, что определяем значение min веса, тогда определим самый короткий путь (D:array [1..n] of integer). Для s,t существует вершина V, для которой расстояние D[t]=D[u]+A[u,t]. Запомним u в стеке, повторим процесс поиска вершины v, такой, что и D[u]=D[v]+A[u,v] и т.д. до тех пор пока не найден ? с конца

В стеке имеем последовательность. D – глобальный массив

Как найти D? Идея любого алгоритма заключается: по заданое матрице смежности весов А, вычисляются первоначальные верхние оценки затем пытаются улучшить (уменьшить) пока это возможно.

Поиск улучшения значений D заключается в нижней вершин u такие что D[u]+A[u,v]<D[u]. Если такая вершина есть, то D[u] можно заменить на значение этой суммы. Алгоритм Дейкстра Дано: G=(V,E), A – матрица смежности с весом дуг. S – вершина ист. Результат: найден массив кротчайшего расстояний D.

Тут формируются: - линия вершин Т, для которых не вычисляется оценка расстояния - минимальное значение D по линии вершин принадлежащих T , считается окончательной оценкой для вершины, на которой даст минимум

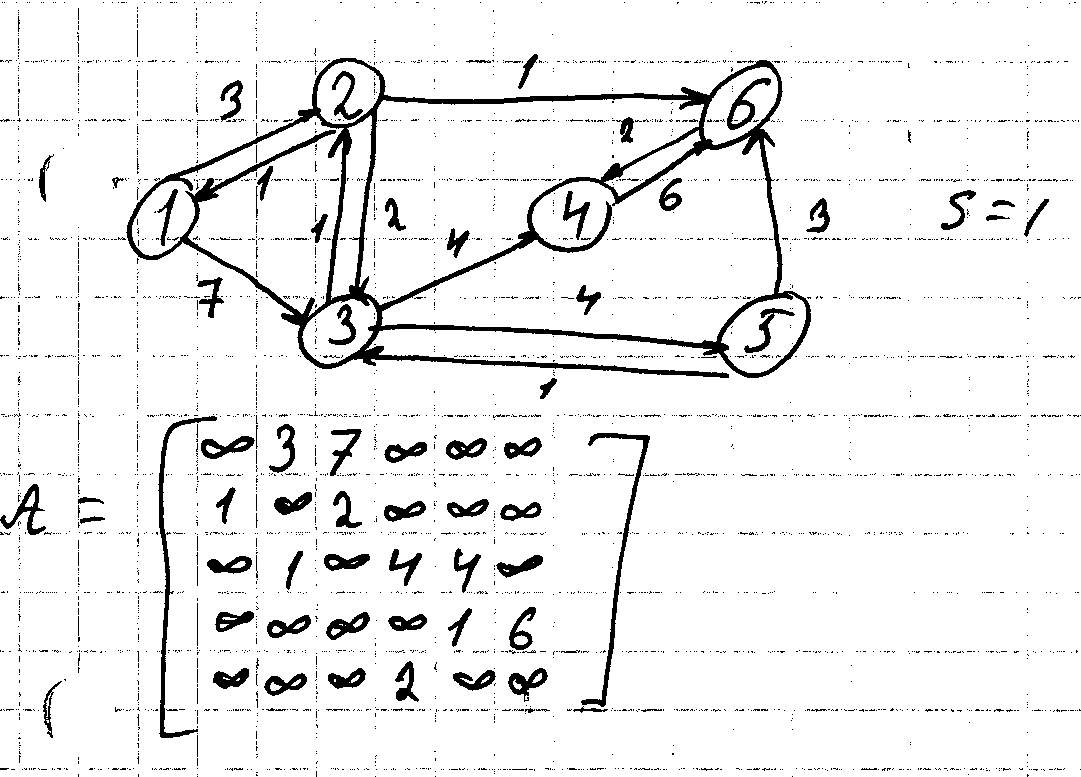
Таблица итераций работы алгоритма улучшения оценок:

Num	D1	D2	D3	D4	D5	D6	T
1	0	3	7	∞	∞	∞	[2.3.4.5.6] N=2, т.е. D2=min T=T-4
2	0	3	5	∞	∞	4	[3,4,5,6] min=D6 T=T-6
3	0	3	5	6	∞	4	[3,4,5] min=D4 -> T=T-3
4	0	3	5	6	7	4	[4,5]->T=T-4
5							T=T-5