Пр. рассмотрим дерево поиска в котором все ключи левого поддерева вершины ti меньше ключа ti , а в правом все ключи больше ti. В таком дереве обнаружить произвольный ключ можно следующим образом:

Начать с корня движемся к левому или правому поддереву на основании одного сравнения с ключом текущей вершины. Поиск пойдет по одному единственному пути от корня к искомой вершине. Если дошли до листа (вершина нет потомков) не обнаружив вершину поиска, значит ее нет в дереве.

Каждая вершина дерева объявляется как запись следующего типа:

Type Ptr=^Node; node=record key:integer; left,right:ptr; end;

Var q,p,r:ptr;

Function locate(t:ptr;x:integer):ptr;

(t<>nill) and (t^.key<>x)

-

End

Locate=t

+

t^.key<x

-

t=t^left

+

t=t^.right

If locate (t,x)=x then (в главной) edit1.text:=’вершина найдена’ else edit1.text:=’вершины нет’

Поиск и включение для деревьев

Рассмотрим случай, когда дерево постоянно только растет. Пр. построение частичного списка слов при анализе текста. Любое слово надо искать в дереве, причем в начале дерево пустое, если слово найдено, то счетчик увеличивается на 1, если нет, то слово включаем в дерево со счетчиком в равной единице. Считаем, что есть уже файл ключей и переменная указывающая на корень дерева поиска, тогда можем сформулировать следующий цикл.

Readln(f,x); (главная) while not eof (f) do begin search(x,root); //процедура readln (f,x); end;

Procedure Search (x:integer; var p:ptr);

Getmem (p,sizeof(node)); p^.key=x p^.count=1 p^.left=nil p^.right=nil

p=nil

- +

x<p.key

-

+ -

search (x,p^left)

x>p^.key

+

search (x,p^.right)

-

End

p^.count=p^.count+1

Этот алгоритм кроме поиска можно использовать как алгоритм сортировки, напоминает прямое включение. Но вместо массива используется дерево, следовательно, нет необходимости передвигать компонент находящийся выше места включения. Если элемент совпал с вершиной, его все равно надо включать.

Исключение из деревьев

Изъятие из упорядоченного дерева вершины с ключом х. Возникает один из 3х случаев.

1. Компонент исключен

2. Компонент с key равным ключом х имеет не более одного потомка

3. Компонент с key равны ключу имеет 2х потомков.

В третьем случае либо на самый правый элемент его левого поддерева нужно найти, либо на самый левый его правый поддерева. Причем они должны иметь не более одного потомка. Реализуем исключение в рекурсивной процедуре delete, в delete учтем все 3 случая. Вспомогательная процедура del будет работать только в 3ем случае, она спускается вдоль правой части левого поддерева элемента q^. Элемент исключаем, и процедура заменяет существенную информацию key и count в элементе q на значение и самые правые компоненты левого поддерева. После чего от r освобождаемся.

Пр.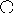

                     10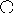

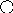
5 15 q (удалить)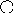

3 8 13 r 18

Получится

10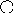

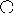
5 13

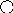
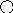
3     8      18

Встает самый правый элемент левого поддерева.

Procedure Delete(x:integer; var p:ptr); var q:ptr;

p=nil

+

Слова нет

+ -

x<p^.key

Delete (x,p^.left)

-

x>p^.key

Delete (x,p^.right))

+ Исключение -

q=p

- -

+

p=q^.left

q^.right=nil

-

q^.left=nil

+

p=q^.right

-

del(q^.left)

getmem(q,0)

End

Procedure Del (var r:ptr);

Delete (p^.right)

r^.right>nil

q^.key=r^.key q^.count=r^.count

q=r

r=r^.left

End

Сбалансированные деревья

Балансировка — это восстановление дерева. Будем рассматривать балансировку после случайного включения. Выход найден в менее строгом определении сбалансированности дерева. Адемсон – Вельский и Ландис (АВЛ – дерево)

Критерии сбалансированности.

Дерево называется сбалансированным, когда высоты 2х поддеревьев каждой из подвершин отличаются не более чем на единицу. У сбалансированных деревьев за время пропорциональное log n, даже в худшем случае можно выполнить такие операции:

1. Найти вершину с заданным ключем

2. Включить новую вершину с заданным ключем

3. Иключить вершину с заданным ключем.

Принцип построение таких деревьев напоминает принцип построения Фибоначчи. Найдем максимальную высоту А для всех сбалансированных деревьев с n вершинами. Возьмем фиксированную высоту h и попытаемся построить сбалансированное дерево с минимальным числом вершин. Обозначим такое дерево с минимальным числом вершин.

Будем брать корень и его поддерево с минимальным числом вершин.

Th T4 To, T1 5 Th(h>1)                                                                                   3       7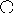

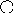
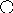
T1 2 T2 3 T3 2 4     6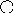

1 2 4                                        1

1

Такие деревья называются деревьями Фибоначчи и строятся следующим образом

1. Пустое дерево с вершиной 0

2. Единственное вершина это дерево с высотой 1

3. Если деревья Фибоначчи Th-1 Th-2, то Th(Th-1,x,Th-2) Th дерево Фибоначчи высотой h

4. Других деревьев Фибоначчи не существует.

No=0; N1=1; Nh=N(h-1)+1+N(h-2) N2=1+1+0=2 N3=2+1+1=4 N4=4+1+2=7