3.1. Интерполяция в системеMatlab.

Цель работы – получить аналитическое выражение функциональной зависимости от аргумента, заданного аналитически или графиком.

Пусть функция задана в виде таблицы (табл. 2). Это зависимость равновесной влажности от относительной влажности воздуха при постоянной температуре.

Таблица 2. Зависимость равновесной влажности от относительной влажности воздуха при постоянной температуре.

ω, %	10,5	17	25	33	41	48	55	61	66,5	71	76	78	82	84,5	87	92	94,5
ωр, %	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	18	20

Создадим и введем два вектора-строки­ и и по полученной таблице построим график:

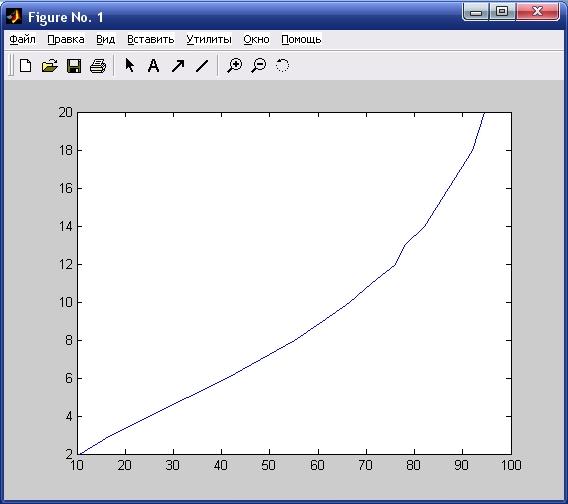
Рис. 4. Экспериментальный график зависимости.

Выбор вида функции интерполяции.

Интерполяция точная в узлах – такая интерполяция, при которой значения функции интерполяции совпадают с ее действительными значениями во всех узлах.

Интерполяция полиномами в среде осуществляется с помощью функции :

Тогда функцией интерполяции будет полином третьей степени

В системе имеется функция вычисления математического выражения при заданных значениях аргументов. Функция имеет вид :

Найдем абсолютную среднеквадратическую погрешность аппроксимации:

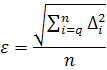
Полученная ошибка очень мала, что подтверждает хорошее совпадение результата интерполяции.

3.2. Интерполяция в средеExcel. Линия тренда. Задачи №1.

Цель работы – получить аналитическую зависимость функции от аргумента (по таблице 3) в среде Excel.

В данной задаче анализируемые данные представлены таблично:

Таблица 3. Зависимость равновесной влажности от относительной влажности воздуха при постоянной температуре.

ω, %	10,5	17	25	33	41	48	55	61	66,5	71	76	78	82	84,5	87	92	94,5
ωр, %	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	18	20

График, построенный по табличным значениям, выглядит следующим образом:

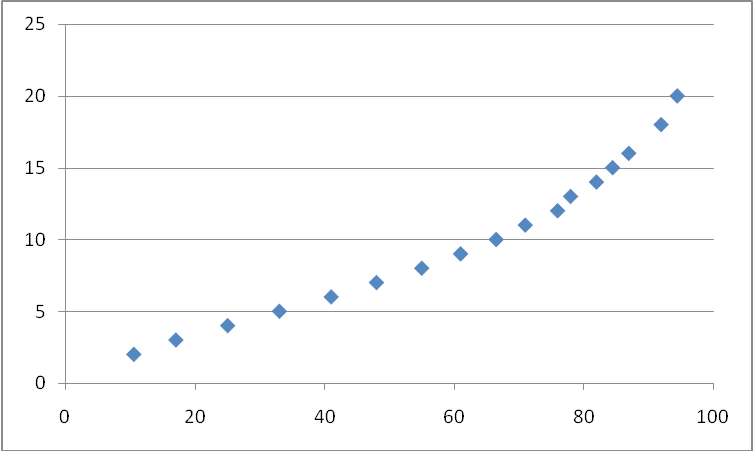
Рис. 5. Графическое отображение табличных значений.

Выбрав в контекстном меню тип линии и ее степень (полиномиальная линия 4-й степени), ставим галки в поле для отображения уравнения и степени достоверности интерполяции на графике.

В результате получаем:

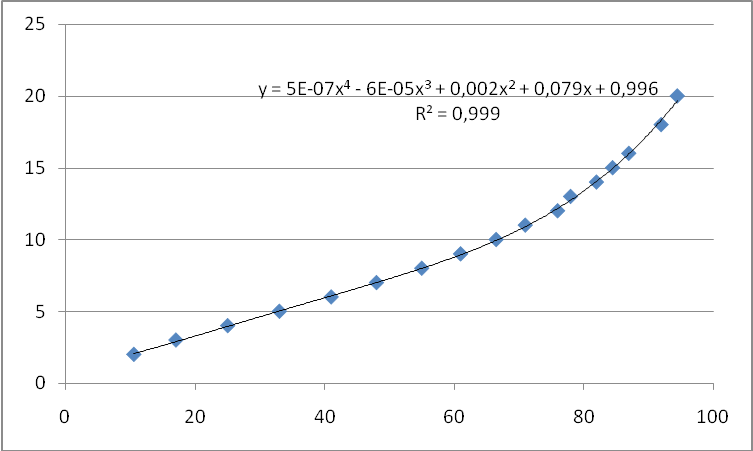
Рис. 6. Кривая интерполяции.

В данном случае не видно выпадающих экспериментальных точек на линии тренда и высока степень достоверности. Для построения интерполяционного полинома, проходящего через все экспериментальные точки, необходимо, чтобы степень полинома была на единицу меньше количества точек. Очевидно, что чем выше степень полинома, тем больше аппроксимирующая кривая приближается к интерполяционному полиному. Однако положительный результат может быть получен и при меньшем количестве точек, что видно из рис. 6. В данном случае степень полинома равна четырем, а количество точек семнадцати. Достоверность аппроксимации (величина достоверности вполне удовлетворяет).

3.3. Интерполяция в средеExcel. Линия тренда. Задача №2.

В этой задаче используются графические данные.

Для решения этой задачи воспользуемся графиком, характеризующим процесс конвективной сушки шпона.

Табл. 4. Зависимость влажности шпона в процессе конвективной сушки.

Продолжительность сушки, мин	0	1	2	3	4	5	6	7	8	9	10	11	12
Влажность шпона, %	80	74	68	58	50	43	36	30	25	20	17	13	10

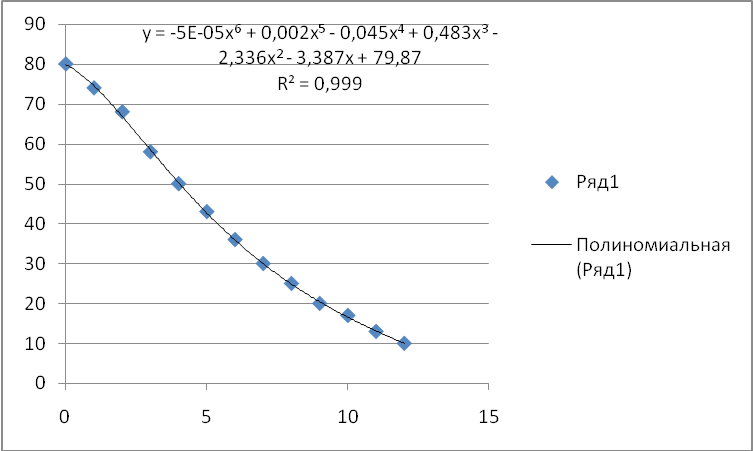
Рис. 7. Кривая интерполяции.

В данном случае не видно выпадающих экспериментальных точек на линии тренда и высока степень достоверности. Для построения интерполяционного полинома, проходящего через все экспериментальные точки, необходимо, чтобы степень полинома была на единицу меньше количества точек. Очевидно, что чем выше степень полинома, тем больше аппроксимирующая кривая приближается к интерполяционному полиному. Однако положительный результат может быть получен и при меньшем количестве точек, что видно из рис. 7. В данном случае степень полинома равна шести, а количество точек тринадцати. Достоверность аппроксимации (величина достоверности вполне удовлетворяет).