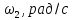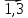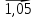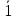- •3. Кинематический анализ ……………………………………….…………..…10
- •3.1. Кинематический анализ кривошипно-ползунного механизма...................12
- •3.1.2. План скоростей механизма кривошипно-ползунного механизма.…......13
- •1.Введение
- •2. Структурный анализ
- •Структурный анализ механизма включает в себя:
- •2.1. Структурный анализ кривошипно-ползунного механизма
- •2.2. Структурный анализ шарнирного четырёхзвенного механизма
- •5. Разбиваем механизм на базовый и группы Асура
- •3. Кинематический анализ
- •3.1. Кинематический анализ кривошипно-ползунного механизма
- •3.1.1. Построение плана положений кривошипно-ползунного механизма методом засечек
- •3.1.2. Построение плана скоростей кривошипно-ползунного механизма
- •3.1.3. Построение плана ускорений кривошипно-ползунного механизма
- •3.2. Кинематический анализ шарнирного четырёхзвенного механизма
- •3.2.1. Построение плана положений шарнирного четырёхзвенного механизма методом засечек
- •Определить масштабный коэффициент по формуле:
- •3.2.2. Построение плана скоростей шарнирного четырёхзвенного механизма
- •3.2.3. Построение плана ускорений шарнирного четырёхзвенного механизма
- •4. Силовой (кинетостатический) анализ
- •4.1. Силовой (кинетостатический) анализ кривошипно-ползунного механизма
- •4.2. Силовой (кинетостатический) анализ шарнирного четырёхзвенного механизма.
- •5. Динамический анализ
- •6. Заключение
- •7. Список используемой литературы
3.1. Кинематический анализ кривошипно-ползунного механизма
3.1.1. Построение плана положений кривошипно-ползунного механизма методом засечек
1.
Определить масштабный коэффициент по
формуле: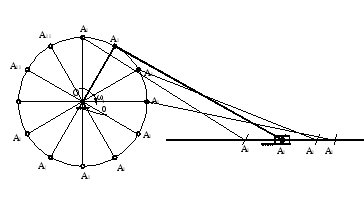
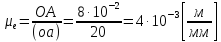
Все дальнейшие построения проводятся с учетом масштабного
c учетом масштабного коэффициента.
Т.е
(AB)=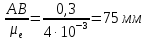 ,
(ОА)=
,
(ОА)=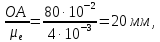 (e)=
(e)=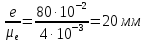
Провести окружность радиусом ОА, которая представляет собой траекторию движения точки А относительно стойки.
Нанести на план траекторию движения точки B относительно стойки – прямая, параллельная линии движения ползуна и проходящая через точку B.
Из точки А0построить дугу окружности радиусом (АВ) до пересечения с траекторией движения точки В относительно стойки.
Место пересечения обозначить В0.
Точку А0соединить с точкой В0.
3.1.2. Построение плана скоростей кривошипно-ползунного механизма
Планом
скоростей звена механизма называют
условное графическое построение,
представляющее собой плоский пучок
векторов с единым общим началом (p)-
называемым полюсом плана скоростей.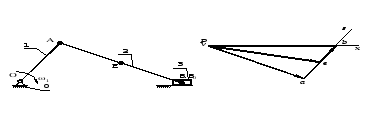
Каждый
вектор, которого изображает абсолютную
скорость точки звена. Вектор
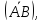 соединяющий концы векторов соединяющий
концы векторов
соединяющий концы векторов соединяющий
концы векторов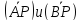 ,
изображает относительную скорость
точек звенаAB.
,
изображает относительную скорость
точек звенаAB.
Произвольно, исходя из удобства размещения на чертеже, выбрать положение полюса плана скоростей P.
Совокупность планов скоростей всех звеньев механизма с единым общим полюсом называется планом скоростей механизма.
Определить величину линейной скорости точки А ведущего звена механизма (кривошипа) из выражения
Vₐ
= ω∙OA=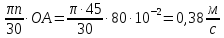
Из
полюса построить вектор абсолютной
скорости точки A
перпендикулярно OA
по направлению угловой скорости![]() .
Длина вектора
.
Длина вектора![]() выбирается
произвольно, исходя из удобства
построений. При этом масштаб плана
скоростей определяется по формуле
выбирается
произвольно, исходя из удобства
построений. При этом масштаб плана
скоростей определяется по формуле
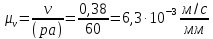 ,
(pa)-выбирается
исходя из значения скорости
,
(pa)-выбирается
исходя из значения скорости
Составить
векторные уравнения для определения
вектора абсолютной скорости точки В.
Движение точки В
является
сложным, поэтому рассмотрим движение
точки В
вокруг
двух центров переноса. Относительно
первого вместе с шатуном 2 , в качестве
центра переноса выбираем точку А,
скорость которой известна. Относительно
второго центра переноса вместе с ползуном
3.
В качестве центра переноса выбираем
точку B0,
находящуюся на стойке, вектор скорости
которой тоже известен![]() .
Система векторных уравнений имеет
вид(Теорема о сложении скоростей в
переносном и относительном движении):
.
Система векторных уравнений имеет
вид(Теорема о сложении скоростей в
переносном и относительном движении):
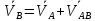
,где ![]() вектор
скорости точки В
относительно
полюса переноса А–относительное
движение (линия его действия известна,
она перпендикулярно ВА).
вектор
скорости точки В
относительно
полюса переноса А–относительное
движение (линия его действия известна,
она перпендикулярно ВА).
![]() вектор
скорости точки В
относительно
полюса переноса B0(линия
его действия известна, она параллельна
линии движения ползуна 2).
вектор
скорости точки В
относительно
полюса переноса B0(линия
его действия известна, она параллельна
линии движения ползуна 2).
Через
конец отрезка ![]() (pa)проведем
линию действия
(pa)проведем
линию действия![]() перпендикулярно
звену AB. Так как мы знаем, что ползун
двигает параллельно
перпендикулярно
звену AB. Так как мы знаем, что ползун
двигает параллельно
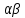 .
То при пересечении прямой, имеющей
начало в (.)a
и перпендикулярно звену AB, и прямой,
отложенной параллельно
.
То при пересечении прямой, имеющей
начало в (.)a
и перпендикулярно звену AB, и прямой,
отложенной параллельно
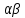 проведенной через (.)p.
Получим (aв),
который обозначает скорость в относительном
движении коэффициента, то есть
проведенной через (.)p.
Получим (aв),
который обозначает скорость в относительном
движении коэффициента, то есть
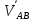 .
Полученный отрезок (pв)-
будет обозначать абсолютную скорость
ползуна, то есть
.
Полученный отрезок (pв)-
будет обозначать абсолютную скорость
ползуна, то есть
 .VAB=(aв)
.VAB=(aв)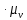 ;
VB=(pв)
;
VB=(pв)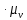 .
Соответственно, получим:
.
Соответственно, получим:
|
Положение |
VAB,м/с |
VB,м/с |
|
1 |
0,39 |
0,1 |
|
2 |
0,315 |
0,42 |
|
3 |
0 |
0,38 |
|
4 |
0,3 |
0,13 |
|
5 |
0,39 |
0,1 |
|
6 |
0,27 |
0,28 |
|
7 |
0 |
0,38 |
|
8 |
0,25 |
0,25 |
Найдем теперь угловую скорость второго звена.
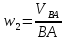
![]() ,соответственно
получим:
,соответственно
получим:
|
Положение |
|
|
1 |
|
|
2 |
|
|
3 |
0 |
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
0 |
|
8 |
|
Направление
угловой скорости шатуна определим
следующим образом. Мысленно перенесем
параллельна самому себе вектор(aв)
на плане скоростей, изображающий
относительною скорость
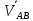 ,на
план положений, поместив его начало в
(.) B.
Наблюдая за движением звена 2 из точки
А, видим, в какую сторону происходит
вращение шатуна.
,на
план положений, поместив его начало в
(.) B.
Наблюдая за движением звена 2 из точки
А, видим, в какую сторону происходит
вращение шатуна.