Контрольная работа №4

171 – 180. Если закон движения точки на прямой задан функцией , то. Для нахождениянужно найти критические точки функции, вычислить значениев критических точках, принадлежащих отрезку, и на концах этого отрезка и выбрать из полученных значений наибольшее по модулю. Точно так же находим.

181 – 190. Функция называется первообразной для функции, если. Совокупность всех первообразных для функцииназывается неопределенным интегралом от функциии обозначается, при этомназывается подынтегральной функцией,– подынтегральным выражением.

Можно доказать, что , где– некоторая первообразная для,– произвольная постоянная.

Для вычисления неопределенных интегралов нужно знать основные свойства, табличные интегралы и методы интегрирования.

Основные свойства неопределенных интегралов:

1. .

2. , где– постоянная, не равная нулю.

3. .

4. .

Свойства 3 и 4 показывают, что операции дифференцирования и интегрирования являются взаимообратными.

Таблица неопределенных интегралов

1)

2)

3)

Если , то.

4)

5)

6)

7)

8)

9)

10)

11)

Все формулы справедливы также в случае, если переменную заменить на некоторую другую функцию. Так, если в формуле 2 заменитьна, то получим,

.

Перейдем к рассмотрению методов интегрирования.

Непосредственное интегрирование (181-190, а)

Преобразование подынтегрального выражения в целях получения табличного интеграла называется непосредственным интегрированием, при этом используется следующая формула:

.

Рассмотрим несколько примеров.

1)

2) .

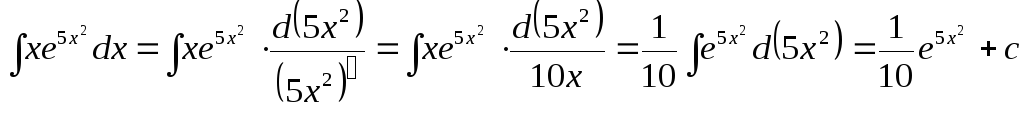3)

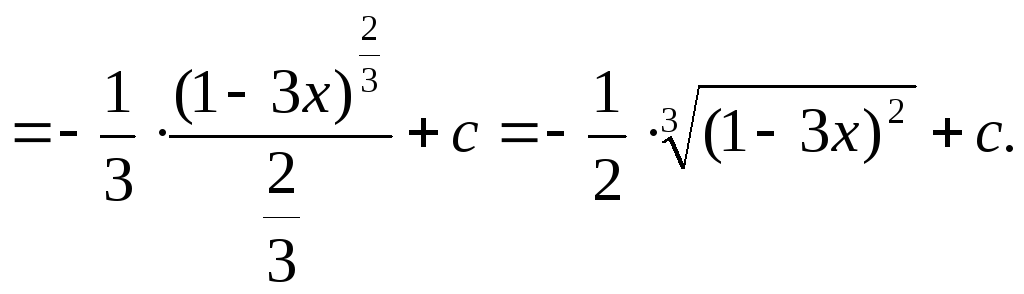
4)

Интегрирование по частям (181-190, б)

Формула интегрирования по частям имеет вид

,

поскольку , то эту же формулу можно записать так:

.

Для того чтобы применить формулу интегрирования по частям, нужно подынтегральную функцию разбить на два множителя, один из них обозначить , другой −. После этого найтии. Для нахождения функциипо заданной производнойможно вычислить неопределенный интеграли затем положить.

При выборе функций иследует помнить, что функцияне должна быть сложной, иначе для нее будет трудно найти первообразную. В качествеобычно выбирают функцию, которая упрощается при дифференцировании, например, логарифмическую или обратную тригонометрическую функцию. В частном случае заможно взять подынтегральную функцию, тогдаи.

Пример. Вычислить .

Решение. Положим . Тогда.

Найдем ;.

Применим формулу интегрирования по частям:

.

Интегрирование подстановкой (181-190, д, е)

В неопределенном интеграле можно сделать подстановку (замену переменной), чтобы получить более простой интеграл.

.

Если подынтегральная функция является иррациональной, то нужно сделать такую подстановку, чтобы новая подынтегральная функция не содержала иррациональностей.

Пример. – интеграл от иррациональной функции.

Сделаем подстановку , тогда.

Таким образом,

.

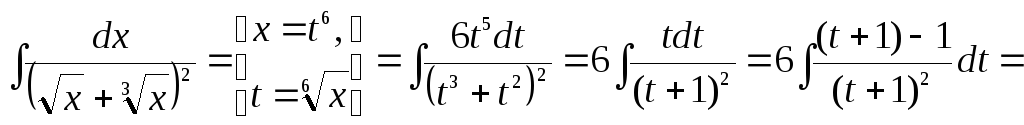
Если подынтегральная функция зависит только от функций и, то можно сделать универсальную тригонометрическую подстановку. В результате подынтегральная функция не будет содержать функцийи, так как

,

,

.

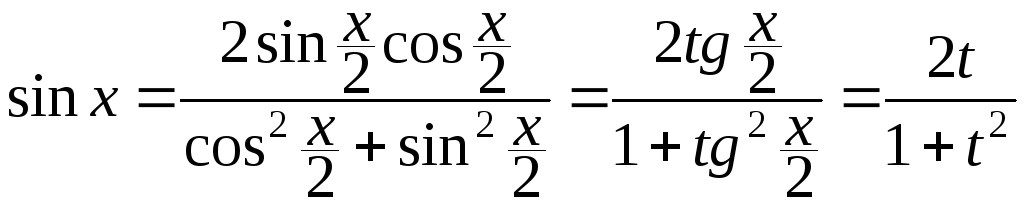Пример.

.

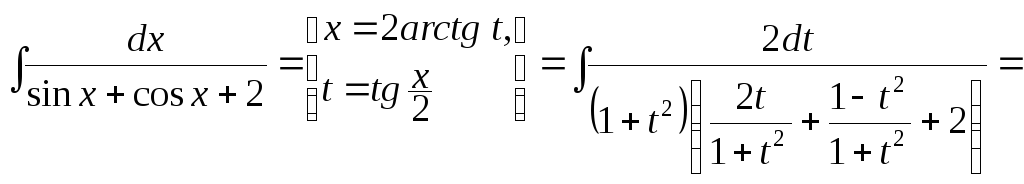
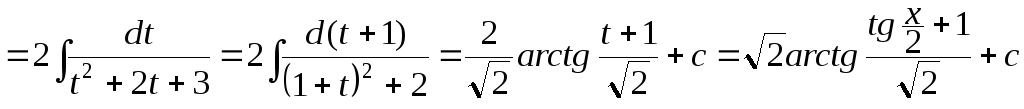Если подынтегральная функция зависит только от , то следует сделать подстановку.

1812190, в. Данные интегралы можно вычислить, не используя универсальную тригонометрическую подстановку. Рассмотрим два примера.

1.

.

2.

.