5. Уравнение кривой в полярных координатах (41-50)

Чтобы в уравнении кривой перейти от полярных координат ,

кдекартовым, используйте формулы:,,, которые получаются из рассмотрения прямоуголь- ного треугольникаОАМ, изображенного на рис. 2.

Пример. Пусть задана кривая уравнением в полярных координатах

.

Решение.

, ,,

, ,.

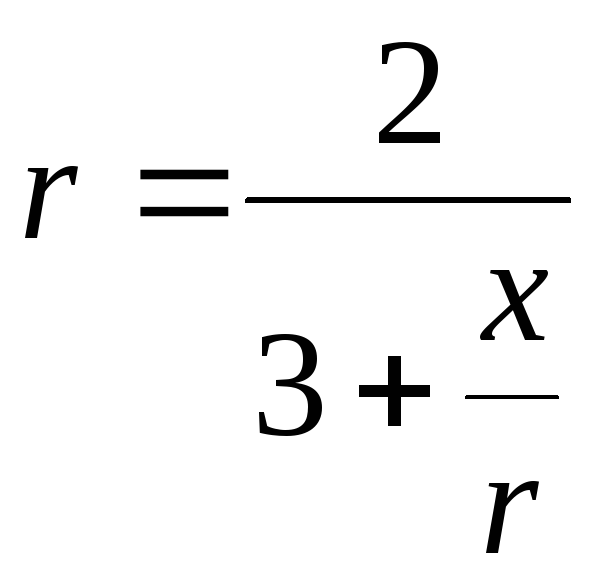–уравнение кривой в декартовых координатах (эллипс).

6. Комплексные числа (51-60)

Комплексным числом называется выражение вида , где– действительные числа,– мнимая единица, удовлетворяющая условию.

Комплексное число изображается точкойплоскости или радиусом-векторомэтой точки (см. рис. 2).Из прямоугольного треугольника ОАМ получаются следующие формулы:

,

где – модуль числа,– аргумент.

Запишем комплексное число в алгебраической, тригонометрической и показательной формах:

.

Комплексные числа в алгебраической форме складываются и умножаются, как многочлены, причем

, ,

При делении комплексных чисел числитель и знаменатель надо умножить на число, сопряженное знаменателю, например:

.

Показательная функция

.

Корень -й степени из комплексного числа

,

.

Пример. Найти все корни уравнения .

Решение. Из уравнения следует, что . Пусть. Это комп-

лексное число изображено на рис. 3 точкойМ (0; 4). Тогда модуль а аргумент . В триго- нометрической форме числоz имеет вид:

.

.

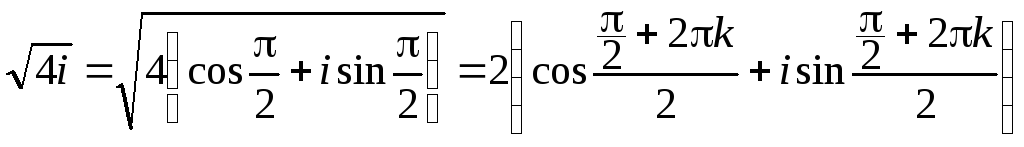Если , то.

Если , то.

Ответ: .

Контрольная работа №2

1. Решение системы линейных уравнений (61-70)

А. Метод Гаусса.

Пример. Решить методом Гаусса систему уравнений

Используя первое уравнение, исключим вначале из второго и третьего уравнений. Для этого сложим первое уравнение, умноженное на -1, со вторым, умноженным на 2. Затем первое уравнение, умноженное на -2, сложим с третьим уравнением.

Получим

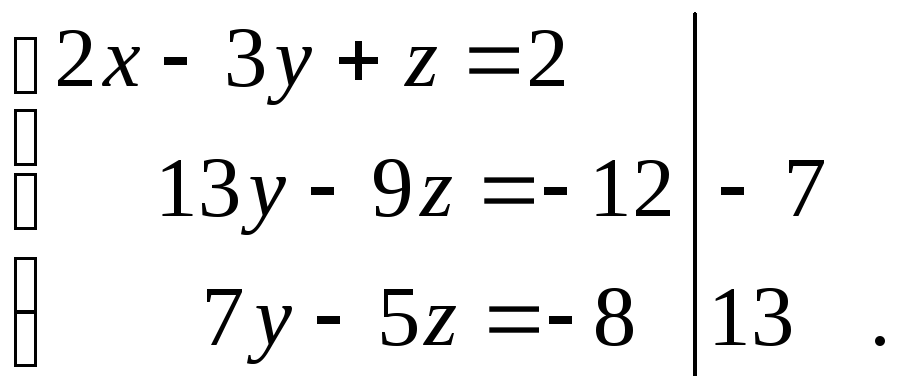
Исключим из третьего уравнения , складывая второе уравнение, умноженное на27, с третьим, умноженным на 13:

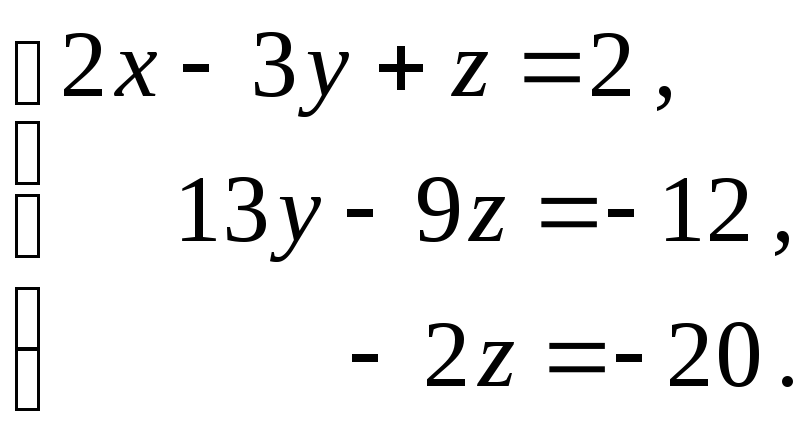
Теперь последовательно находим и:

, ,;

, ,.

Ответ: ,,.

Б. Матричный способ.

Рассмотрим вначале действия над матрицами.

Матрицей размером называется таблица чисел, содержащаястрок истолбцов.

Если , то получаем квадратную матрицуго порядка.

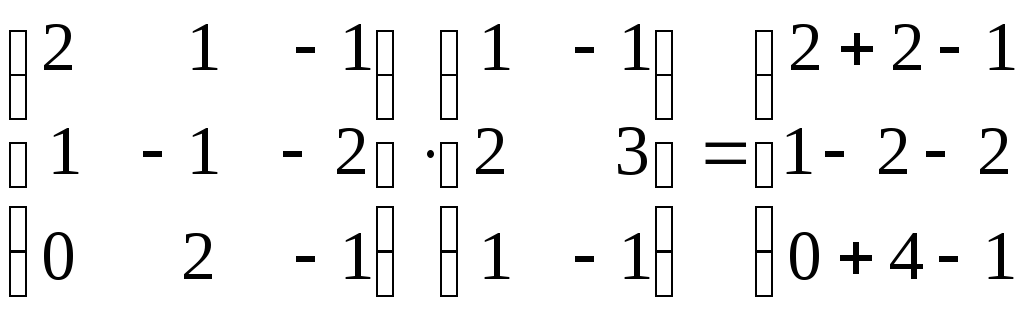
При умножении матриц каждая строка первой матрицы умножается на каждый столбец второй.

При умножении строки на столбец перемножаются их первые элементы, вторые и т.д. и результаты складываются. Поэтому можно умножать только такие матрицы, у которых число столбцов первой матрицы равно числу строк второй.

Примеры.

,

.

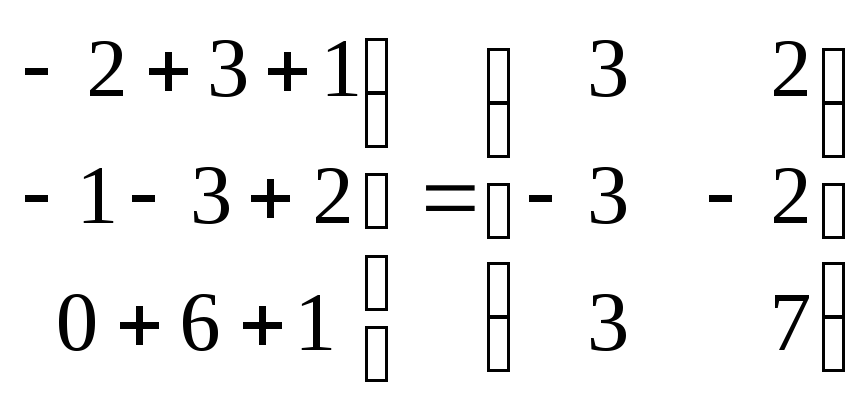Матрица называется обратной по отношению к квадратной матрице, если

.

Покажем, как найти обратную матрицу .

Пусть

.

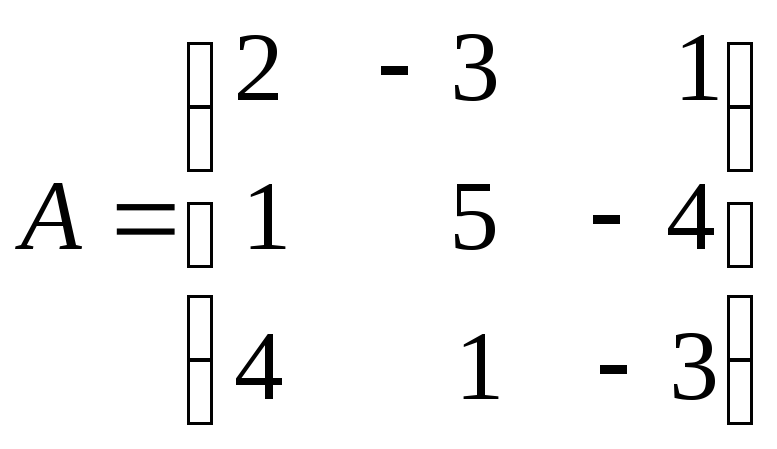а) .

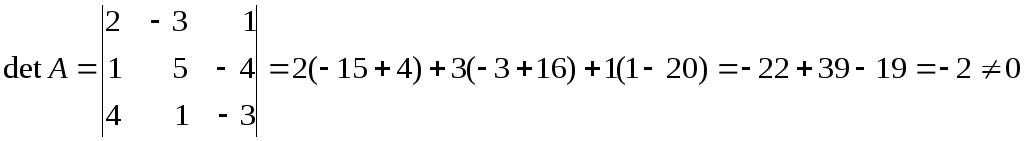Так как , тосуществует.

б) Пусть - элемент матрицы, расположенной в-й строке и-м столбце. Если в определителевычеркнуть строку и столбец с элементом, то получим дополнительный минорэлемента. Это определитель 2-го порядка.

Составим матрицу из дополнительных миноровэлементов матрицы:

.

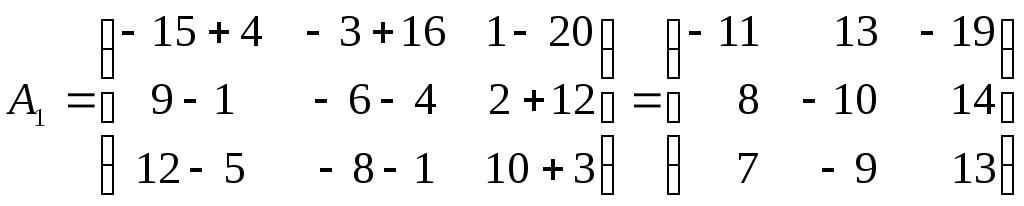в) Составим матрицу из алгебраических дополненийэлементов.

если  четное число,

если  нечетное число .

.

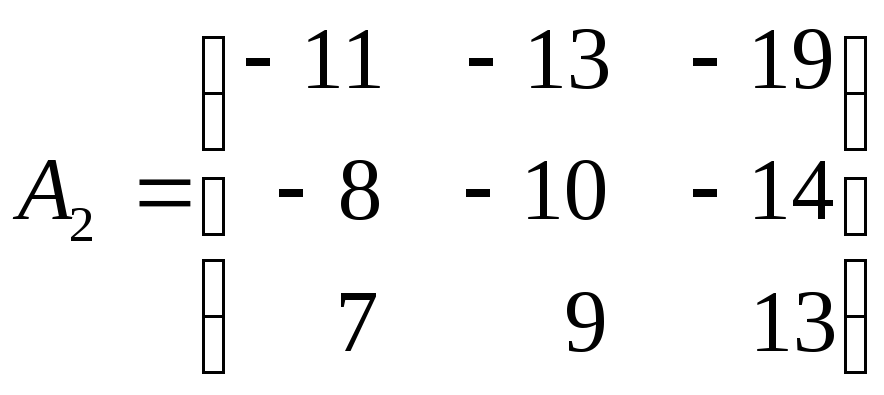г) Транспонируем матрицу , т.е. строки поменяем местами со столбцами:

.

Обратная матрица определяется формулой

,

.

Покажем, как решается система уравнений матричным способом.

Пример. Решить систему

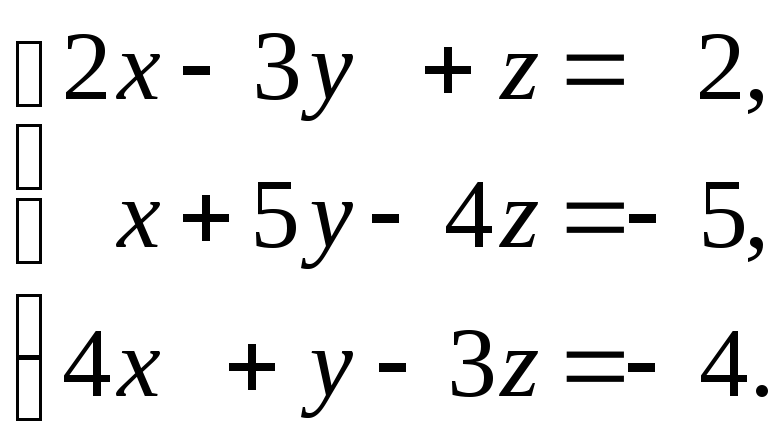
Решение. Обозначим:

, ,.

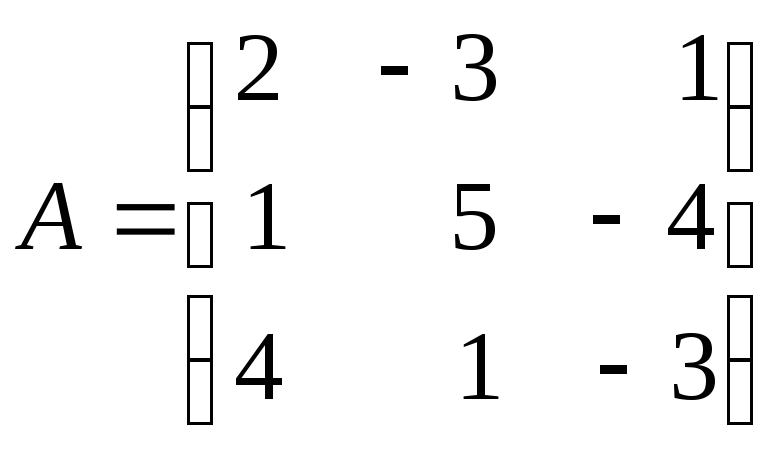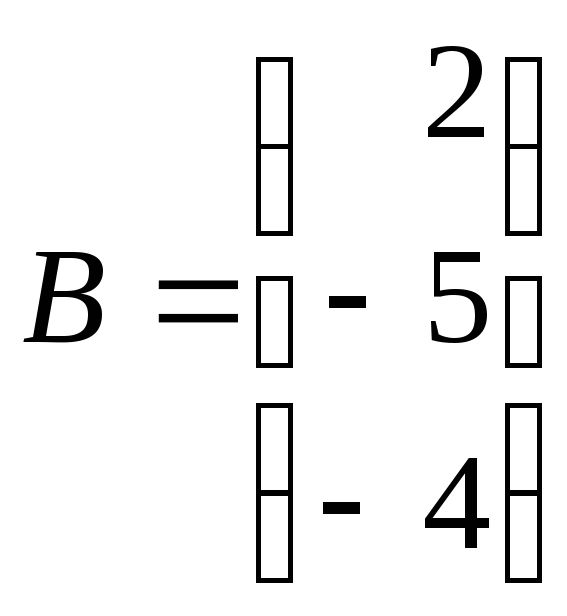Получаем матричное уравнение .

Его решение , т.е.

.

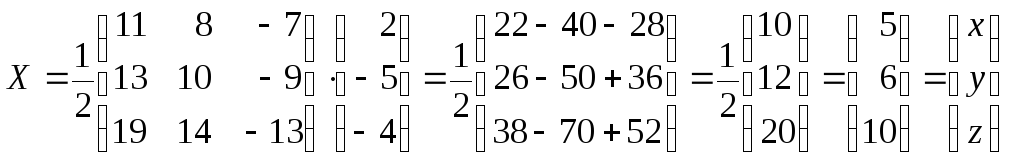Ответ: