Циркуляция скорости

Вихрь скорости, также как и угловая скорость жидкой частицы, не поддается непосредственному измерению приборами. Нельзя непосредственно измерить и интенсивность вихревой трубки. Однако эту величину можно оценить по другой величине, называемой циркуляцией скорости.

Если в пространстве задано поле вектора и выбрана кривая L, для которой указано направление ее обхода, то линейным интегралом вектора по линии L называется криволинейный интеграл

,

где А_ - проекция вектора на касательную к L, проведенную в направлении обхода.

Это выражение можно записать в следующем виде

.

Физический смысл линейного интеграла особенно прост, если - поле сил. В этом случае линейный интеграл по L равен работе, совершаемой полем, когда точка, на которую действует сила, движется по кривой L.

Если L – замкнутая линия, то линейный интеграл называется циркуляцией.

Циркуляцией скорости по кривой L называется интеграл

. (9.10)

Если контур L замкнут, то циркуляция по контуру определяется выражением

. (9.11)

Для плоского течения

.

Рассмотрим замкнутый контур в виде прямоугольника, находящегося в плоскости xOy (рис.9.8).

Ц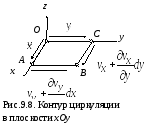иркуляция скорости по контуру ОАВСО составит

(9.12)

Так как , и , то

.

Рассматривая циркуляцию скорости в других плоскостях, окончательно получим

. (9.13)

Здесь - нормаль к поверхности s.

Выражение (9.13) соответствует теореме Стокса:

Циркуляция по произвольному контуру равна сумме интенсивностей вихрей, пронизывающих поверхность, натянутую на контур.

Лекция 10. ПОТЕНЦИАЛЬНОЕ ДВИЖЕНИЕ ЖИДКОСТИ

Потенциал скорости

Сущность теоремы Стокса, по существу, сводится к утверждению о равенстве числовых значений интенсивности вихря и циркуляции, т.е. . С другой стороны, при равенстве нулю вихря скорости, т.е. , в жидкости наблюдается безвихревое движение. Для этого режима течения обязательным условием является . Так как

то отсутствие в жидкости вихрей обеспечивается при равенстве смешанных производных

(10.1.)

Из математики известно, что если функция дифференцируема, то выражение

(10.2)

является полным дифференциалом в том случае, если

(10.3)

В этом случае

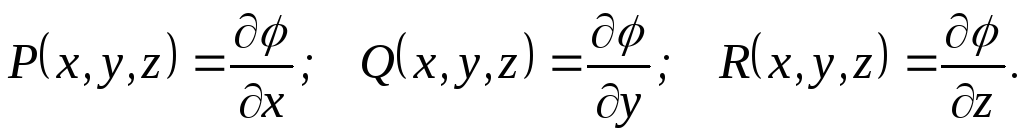(10.4)

Из (10.1) и (10.4) следует, что для безвихревого движения жидкости существует некоторая величина , для которой должны выполняться соотношения

(10.5)

По предложению Гельмгольца функцию  называют потенциалом скорости. Скорость движения частицы можно разложить по координатным осям в виде , что соответствует выражению

. (10.6)

Для многих задач гидромеханики необходимо знать поля скоростей жидкости в рабочей зоне установки. Использование потенциала скорости позволяет задать поля скоростей v_x, v_y, v_z с помощью только одной величины , что существенно упрощает расчеты.

Так как для несжимаемой жидкости в отсутствии источников и стоков , то для потенциального течения

(10.7)

или

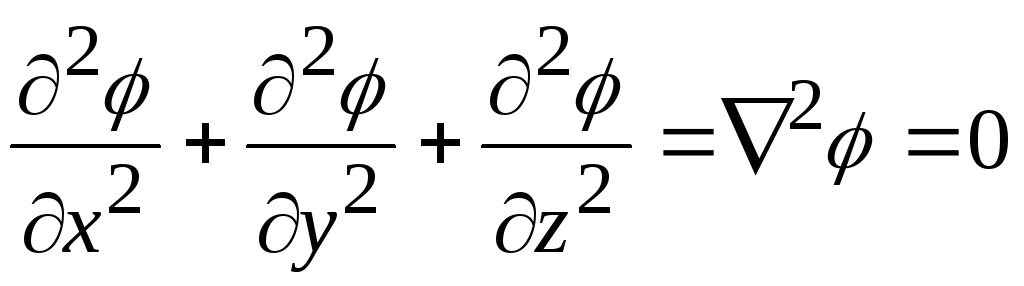. (10.8)

Выражения (6.7) и (6.8) называются уравнениями Лапласа. Как и любое дифференциальное уравнение, уравнение Лапласа имеет бесчисленное множество решений. Для получения однозначного решения необходимо задать граничные условия. Обычно принимают, что при обтекании тела или при движении в канале с твердыми стенками скорость на стенке , а вдали от стенки или тела равна скорости невозмущенного потока .

Выражение для циркуляции скорости в потенциальном потоке приобретает простой вид. Выделим в пространстве произвольную кривую АВ. Циркуляция скорости по этой кривой

.(10.9)

Это означает, что циркуляция скорости по кривой АВ не зависит от формы кривой и равна разности потенциала скорости в конечных точках дуги. В том случае, когда точки А и В совпадают, т.е контур замкнутый и функция  однозначна, то циркуляция скорости в потенциальном потоке по замкнутому контуру равна нулю.