
- •Предмет механики. Механическое движение. Сила, как результат механического взаимодействия между телами.
- •2. Упрощенные модели (абстракции механики), структура механики.
- •Основные понятия: равновесие тела, система сил, основные задачи статики.
- •Аксиомы статики.
- •Понятие о связях и их реакциях. Аксиома связей.
- •Аналитический способ определения равнодействующей системы сходящихся сил.
- •Условия равновесия системы сходящихся сил в различных формах.
- •Теорема о равновесии трех непараллельных сил.
- •Алгебраический момент силы относительно точки (центра).
- •Векторный момент силы относительно точки (центра).
- •Момент силы относительно оси.
- •Зависимость между моментами силы относительно оси и точки, лежащей на этой оси.
- •Аналитические выражения моментов силы относительно координатных осей.
- •Теорема о сложении пар.
- •Условия равновесия системы пар.
- •Характеристические величины системы сил, главный вектор, главный момент, характеристическое произведение и их аналитическое определение.
- •Лемма о параллельном переносе силы из одной точки тела в другую.
- •Основная теорема статики об эквивалентности системы сил, силе и паре сил.
- •Приведение системы сил к равнодействующей. Теорема Вариньона о моменте равнодействующей
- •Теорема о необходимых и достаточных условиях равновесия произвольной системы сил.
- •Аналитические условия равновесия произвольной пространственной системы сил.
- •Условия равновесия произвольной плоской системы сил в трех формах.
- •Условия равновесия параллельных сил.
- •Общие формулы для координат центра тяжести твердого тела.
- •Формулы для определения координат центра тяжести однородных тел.
- •Метод симметрии определения положения центра тяжести.
- •Метод разбиения и метод дополнения при определении положения центра тяжести.
- •Предмет кинематики. Основные задачи кинематики точки.
- •Три способа задания движения точки.
- •Определение скорости точки при векторном способе задания ее движения.
- •Определение ускорения точки при векторном способе задания ее движения.
- •Определение законов равномерного и равнопеременного движения точки.
- •Векторные формулы для определения скоростей и ускорений точек вращающегося твердого тела.
- •Уравнения движения плоской фигуры или уравнения плоского движения тела.
- •Разложение движения плоской фигуры на простейшие движения.
- •Теорема о скорости любой точки плоской фигуры как сумме скорости полюса и вращательной скорости этой точки вокруг полюса. Следствия.
- •Мгновенный центр скоростей. Теорема существования и единственности мцс.
- •Теорема об определении скорости точек плоской фигуры с помощью мцс. Следствия.
-
Уравнения движения плоской фигуры или уравнения плоского движения тела.
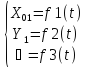
-
Разложение движения плоской фигуры на простейшие движения.
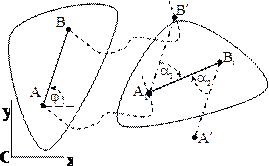 Движение
плоской фигуры можно разложить на
поступательное, вместе с полюсом, и
вращательное вокруг полюса. Полюсом
называем произвольную точку, выбранную
из каких-либо соображений для описания
плоского движения.
Движение
плоской фигуры можно разложить на
поступательное, вместе с полюсом, и
вращательное вокруг полюса. Полюсом
называем произвольную точку, выбранную
из каких-либо соображений для описания
плоского движения.
Для
доказательства рассмотрим два положения
плоской фигуры в моменты
времени ![]() и
и ![]() (рис.1.10).
Переместим фигуру поступательно из
положения
(рис.1.10).
Переместим фигуру поступательно из
положения ![]() в
положение
в
положение ![]() .
При этом точка
.
При этом точка ![]() описывает
такую же траекторию как и точка
описывает
такую же траекторию как и точка ![]() .
Затем повернём фигуру вокруг точки
.
Затем повернём фигуру вокруг точки ![]() на
угол
на
угол ![]() так,
чтобы точка
так,
чтобы точка ![]() заняла
положение
заняла
положение ![]() .
Перевод фигуры из начального положения
в конечное можно произвести различными
способами, выбирая за полюс вместо точки
А любую другую, например, точку В. Заметим,
что при этом поворот будет осуществляться
на тот же угол и в том же направлении.
Т. е. последнее из уравнений движения
плоской фигуры является инвариантным
(независимым) от выбора полюса. Значит
и угловая скорость как производная от
угла поворота не зависит от выбора
полюса. Поступательное движение можно
принять за переносное, а вращательное
— за относительное.
.
Перевод фигуры из начального положения
в конечное можно произвести различными
способами, выбирая за полюс вместо точки
А любую другую, например, точку В. Заметим,
что при этом поворот будет осуществляться
на тот же угол и в том же направлении.
Т. е. последнее из уравнений движения
плоской фигуры является инвариантным
(независимым) от выбора полюса. Значит
и угловая скорость как производная от
угла поворота не зависит от выбора
полюса. Поступательное движение можно
принять за переносное, а вращательное
— за относительное.
-
Теорема о скорости любой точки плоской фигуры как сумме скорости полюса и вращательной скорости этой точки вокруг полюса. Следствия.
Скорость любой точки плоской фигуры равна геометрической сумме скоростей полюса и вращательной скорости этой точки вокруг полюса.
![]()
Доказательство: Пусть плоская фигура движется в её плоскости.
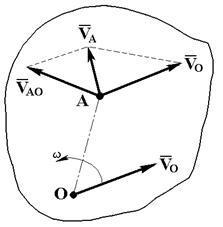
Примем точку О за полюс.
Считаем поступательное движение фигуры вместе с полюсом за переносное, а вращательное вокруг полюса за относительное. Тогда скорость точки А
![]()
![]() ,
так как переносное движение поступательное,
следовательно, переносные скорости
всех точек равны скорости полюса.
,
так как переносное движение поступательное,
следовательно, переносные скорости
всех точек равны скорости полюса.
![]() .
.
![]()
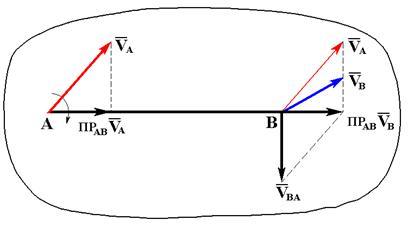
на прямую, соединяющую эти точки.
Проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны.
![]()
![]()
Спроецируем на АВ:
![]()
![]()
-
Мгновенный центр скоростей. Теорема существования и единственности мцс.
) Мгновенным центром скоростей (МЦС) называется такая точка плоской фигуры, скорость которой в данный момент времени равна нулю.
Теорема: в
каждый момент движения фигуры, когда
ее
 существует
МЦС причем единственный .
существует
МЦС причем единственный .
В каждый момент движения плоской фигуры, когда угловая скорость ≠0, существует причем единственный мгновенный центр скоростей.
-
Теорема об определении скорости точек плоской фигуры с помощью мцс. Следствия.
) Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.
Легко убедиться,
что если фигура движется непоступательно,
то такая точка в каждый момент
времени t существует
и притом единственная. Пусть в момент
времени t точки А и В плоской
фигуры имеют скорости ![]() и
и ![]() ,
не параллельные друг другу (рис.6). Тогда
точка Р,
лежащая на пересечении перпендикуляров Аа к
вектору
,
не параллельные друг другу (рис.6). Тогда
точка Р,
лежащая на пересечении перпендикуляров Аа к
вектору ![]() и Вb к
вектору
и Вb к
вектору ![]() ,
и будет мгновенным центром скоростей так
как
,
и будет мгновенным центром скоростей так
как ![]() .
В самом деле, если допустить,
что
.
В самом деле, если допустить,
что ![]() ,
то по теореме о проекциях скоростей
вектор
,
то по теореме о проекциях скоростей
вектор ![]() должен
быть одновременно перпендикулярен
и АР (так
как
должен
быть одновременно перпендикулярен
и АР (так
как ![]() )
и ВР (так
как
)
и ВР (так
как ![]() ),
что невозможно. Из той же теоремы видно,
что никакая другая точка фигуры в
этот момент времени не может иметь
скорость, равную нулю.
),
что невозможно. Из той же теоремы видно,
что никакая другая точка фигуры в
этот момент времени не может иметь
скорость, равную нулю.
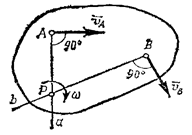
Рис.6
Если
теперь в момент времени ![]() взять
точку Р за
полюс, то скорость точки А будет
взять
точку Р за
полюс, то скорость точки А будет
![]()
так
как ![]() .
Аналогичный результат получается для
любой другой точки фигуры. Следовательно,
скорости точек плоской фигуры определяются
в данный момент времени так, как если
бы движение фигуры было вращением вокруг
мгновенного центра скоростей. При этом
.
Аналогичный результат получается для
любой другой точки фигуры. Следовательно,
скорости точек плоской фигуры определяются
в данный момент времени так, как если
бы движение фигуры было вращением вокруг
мгновенного центра скоростей. При этом
![]()
![]()
Из
равенств, следует еще, что ![]() точек
плоской фигуры пропорциональны их
расстояниям от МЦС.
точек
плоской фигуры пропорциональны их
расстояниям от МЦС.
