3. Перемещения. Линейные и угловые деформации. Деформированное состояние. Принцип начальных размеров.

Под действием внешних сил твердые тела изменяют свою геометрическую форму, а точки тела неодинаково перемещаются в пространстве. Вектор , имеющий свое начало в точке А недеформированного состояния, а конец в т. деформированного состояния, называется вектором полного перемещения т. А (рис. 1.5, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.

Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформированного состояния, расположенные на расстоянии S друг от друга (рис. 1.5, б).

Рис. 1.5

Пусть в результате изменения формы тела эти точки переместились в положение А¢ и В¢, соответственно, а расстояние между ними увеличилось на величину DS и составило S + DS. Величина

1.6)

называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей xyz, то в обозначения соответствующих проекций линейной деформации вводятся индексы ex , ey , ez .

Линейные деформации ex , ey , ez характеризуют изменения объема тела в процессе деформирования, а формоизменения тела - угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрезками ОD и ОС (рис. 1.5, б). При действии внешних сил указанный угол DOC изменится и примет новое значение D¢O¢C¢. Величина

(Ð DOC - Ð D¢O¢C¢) = g (1.7)

называется угловой деформацией, или сдвигом в точке О в плоскости СОD. Относительно координатных осей деформации сдвига обозначаются gxy , gxz , gyz .

Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформированное состояние в точке.

Линейные деформации, как правило, сопровождаются изменением объема тела.

Угловые деформации характеризуются изменением углов наклона γ=α+β граней элементарного параллелепипеда (рис. 3.10). В результате угловой деформации происходит взаимное смещение параллельных граней, то есть сдвиг. Относительный сдвиг γ, может служить характеристикой угловой деформации. При угловых деформациях (сдвигах) изменяется только форма тела, а объем остается неизменным.

Линейная деформация связана, в основном, с действием нормальных напряжений, а деформация сдвига определяется, главным образом, касательными напряжениями. Так, при одноосном растяжении бруса изменяется угол между площадками, где действуют касательные напряжения. Углы между поперечными и продольными площадками, где действуют только нормальные напряжения, остаются прямыми.

Если по граням элемента действуют только касательные напряжения, то такой элемент будет испытывать только деформацию сдвига. Такая деформация называется чистым сдвигом (рис.3.11). Линейное смещение δ одной грани относительно противоположной называется абсолютным сдвигом, а отношение δ к расстоянию между этими гранями h - относительным сдвигом. Отношение δ/h равно тангенсу угла сдвига γ. Вследствие малости угла γ можно принять tgγ≈γ. Подобно тому, как при растяжении имеет линейная зависимость между σ и ε (1.4), при сдвиге наблюдается линейная зависимость между τ и γ, представляющая закон Гука при сдвиге

(3.34)

где G - модуль упругости при сдвиге или модуль упругости второго рода. Его размерность Н/м2.

Всякая деформация связана со смещением точек тела, но не всякое смещение точек тела есть его деформация. Смещение точек тела без изменения их взаимного расположения есть перемещение тела. Смещение точек тела с изменением их взаимного расположения есть деформация тела.

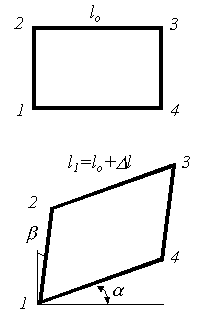
Рис.3.11. Деформация чистого сдвига

Вокруг каждой точки тела можно мысленно выделить бесчисленное множество различно ориентированных элементарных параллелепипедов; у каждого из них будут свои линейные и угловые деформации. Совокупность всех линейных и угловых деформаций в точке есть деформированное состояние в этой точке тела.

Относительные деформации в направлении координатных осей x, y, z (1,2,3) обозначаются εx, εy, εz (ε11, ε22, ε33). Угловые деформации характеризуются углами сдвига, представляющими собой изменение первоначально прямого угла между парой ортогональных отрезков, исходящих из данной точки. Углы сдвига в координатных плоскостях обозначаются γxy, γyz, γxz (2ε12, 2ε23, 2ε13). Линейные деформации в направлении координатных осей прямоугольной системы координат и углы сдвига в координатных плоскостях называются компонентами деформаций в данной точке тела. Как компоненты напряжений полностью определяют напряженное состояние в точке тела, так и компоненты деформаций полностью определяют деформированное состояние в точке тела.

Имеет место полная аналогия в математических зависимостях и свойствах теории напряженного и теории деформированного состояний. При этом матрица компонент деформированного состояния образуется из матрицы компонент напряженного состояния (3.7) заменой нормальных напряжений относительными линейными деформациями, а касательных напряжений – сдвигами, с той лишь поправкой, что касательные напряжения заменяются не на γ, а на γ/2:

(3.35)

Относительная деформация по любому направлению, величины и направления главных деформаций, определяются по аналогии с методами рассмотренными выше для напряженного состояния. В изотропном теле направления главных осей напряженного и деформированного состояний совпадают.

Принцип начальных размеров

Деформированное состояние

ным упругопластическим деформациям будут выше, чем по местным и номинальным напряжениям, а также по предельным нагрузкам. Переход к расчетам по деформационным критериям прочности важен и тем, что в практике создания высоконагруженных машин и конструкций все шире применяют экспериментальные методы определения местных напряженно-деформированных состояний средствами тензометрии, голографии, интерферометрии. При этом непосредственно измеряют перемещения и деформации, пересчет которых в напряжения при упругопластическом деформировании может оказаться достаточно сложным.

Приведенные выше уравнения (1.42)-(1.141), описывающие поля номинальных и местных напряженно -деформированных состояний при наличии конструктивной концентрации напряжений и трещин в упругой и упругопластической областях позволяют рассмотреть условия образования и развития разрушения с использованием силовых, деформационных и энергетических критериев разрушения.

— уточненное определение физических напряженно-деформированных состояний (ён, ан, emax, ётахк) в упругой и упруго пластической областях (с применением методов тензометрии, термометрии, голографии, муара, интерферометрии);

Снижение указанных запасов возможно на основе проведения натурных или полномасштабных модельных испытаний до разрушения, уточненного расчетного и экспериментального анализа напряженно-деформированных состояний при термомеханическом эксплуатационном нагружении.

Задача об определении сопротивления малоцикловому разруше нию при температурах, более высоких, чем указанные, когда цикли ческие и пластические деформации сочетаются с деформациям! ползучести, существенно усложняется. В настоящее время осутдеств ляются интенсивные экспериментальные исследования уравненш состояния и критериев разрушения при длительном циклическол нагружении в условиях однородных напряженных состояний npi жестком и мягком нагружении. Результаты этих исследований широко освещены в литературе. Однако, несмотря на большой объеъ экспериментальных работ, пока не удалось разработать общеприня тые предложения по кривым длительного циклического деформиро вания и разрушения; это не позволяет перейти к расчетной оценк< напряженных и деформированных состояний в элементах конструк ций для определения их прочности и долговечности на стадии обра зования трещин и тем более на стадии их развития [41, 42].

Расчеты прочности при циклическом (мало- и многоцикловом) нагружении по образованию трещин оказываются сложными и трудоемкими как на стадии определения напряженно-деформированных состояний, так и на стадии определения долговечности. Схема такого расчета показана на рис. 4.18. Расчет сводится к определению запасов по предельным нагрузкам про и предельным местным деформациям пео (амплитудам деформаций ёвтах) для заданного эксплуатационного числа циклов нагружения N9, а также запасов по числу циклов NQ на

— разработка методов и средств комплексных физико-механических исследований напряженно-деформированных состояний и механизмов деформирования и разрушения металлических материалов на макро- и микроуровне в широком диапазоне температур;

— разработка методов расчета напряженно-деформированных состояний элементов конструкций, долговечности и живучести машин и сооружений;

— формирование методов аналитического и численного определения напряженно-деформированных состояний в зонах конструктивной концентрации напряжений и деформаций;

На базе уравнений (6.42)- (6. 44) было рекомендовано в расчетах циклических напряженно-деформированных состояний использовать обобщенные степенные уравнения

В монографии представлены результаты многолетних исследований автора. Во второй части анализ прочности и ресурса развит на область оценки характеристик техногенной безопасности. Рассмотрены методические особенности комплексных экспериментальных исследований напряженно-деформированных состояний в условиях различного сочетания механических, тепловых, электромагнитных, аэрогидродинамических нагрузок для штатных и аварийных режимов. Приведены исходные данные для расчетного определения показателей прочности, ресурса и безопасности для объектов тепловой, атомной и термоядерной энергетики, ускорителей, сосудов, трубопроводов и техники северного исполнения. Даны научно-методические рекомендации по оценке прочности, ресурса и безопасности технических систем.

Воздействия на массив (особенно отбойка горной породы) изменяют его напряженно-деформированное состояние и приводят к образованию зоны концентрации напряжений и возникновению предельных состояний и необратимых деформаций. В этой зоне накапливаются запасы энергии упругих деформаций и газа, которые под влиянием инициирующего воздействия внешней силы (иногда даже незначительной) реализуются в выбросе.

Если провести циклическое деформирование упругодиссипативно-го элемента по закону х = xmcos®t, то обнаруживается различие линий нагрузки и разгрузки (рис. 6.31) на диаграмме сила — смещение: точка, изображающая напряженное и деформированное состояние, описывает замкнутую кривую — петлю гистерезиса. Площадь, ограниченная петлей гистерезиса, выражает энергию ел рассеянную за один цикл демпфирования и равную работе диссипативных сил:

В формуле (3.1) неизвестной величиной является радиус R кривизны серединной поверхности оболочки, который полностью определяется пластическими свойствами материала мембраны. Очевидно, чем пластичнее материал (до некоторых пределов) при всех прочих равных условиях, тем до меньшего радиуса R сможет выпучиться мембрана перед разрывом, и поэтому разрушение такой мембраны произойдет при большем давлении Рс. Общепринятой мерой пластичности материала является относительное удлинение 6 при разрыве, которое наряду с ОВР приводится в справочной литературе как одна из основных его механических характеристик. Однако величиной б можно характеризовать предельно деформированное состояние материала, нагруженного только одноосным растягивающим усилием.

Таким образом, предельно деформированное состояние одно-осно растянутого прямоугольного стержня можно характеризо-зать не величиной б, а функционально связанной с ней' величиной v. В случае двухосного растяжения в соответствии с указанным допущением разрушение материала произойдет при условии, что деформация в направлении, перпендикулярном плоскости приложения внешних нагрузок, достигнет величины v, удовлетворяющей соотношению (3.2). Сказанное удобно пояснить, используя рис. 3.10,6: если элемент размерами a, b и I подвержен двухосному растяжению силами N и М, то предельно деформированное состояние его наступит, когда размер а подвергнется относительной деформации v.

В настоящее время моделирование применяется при разработке или уточнении методов расчета на прочность и устойчивость, при проверке правильности результатов статического расчета, а в отдельных случаях — при замене аналитического расчета экспериментальным, при невозможности сделать аналитический расчет, при-различных изысканиях, связанных с выбором наиболее рационального конструктивного решения [71]. Оно может быть использовано-не только для проверки расчета, но и для выявления причин разрушения конструкций (подкрановые конструкции, радиомачты: и др.). Для опор линий электропередач (ЛЭП) установлен порядок обязательного испытания натурных конструкций новых систем-с доведением конструкции до разрушения. Моделирование применяется в самой начальной стадии создания проекта и дает возможность выявить напряженное и деформированное состояние конструкций. Насколько нам известно, примеров моделирования аварий других гражданских и промышленных сооружений и имитации аварий на моделях нет.

В результате численного анализа МКЭ были получены изополосы напряженно-деформированного состояния (рис. 5), кроме того, были реализованы анимационные картинки (деформированное состояние) для представления работы участка трубопровода под нагрузкой. На рис.5 показано распределение изополос ovon в элементе участка трубопровода в случае начала разрушения от внутреннего давления, когда длина трещины достигает значения / = 0,5 м.

Осуществлено методическое обеспечение эксплуатационной технологичности конструкций печей и топки в ТС СП, позволяющее стабилизировать напряженно-деформированное состояние и температурные поля КСП при эксплуатации.

являются зоны концентрации напряжений (КН) и деформаций, возникающих от рабочих нагрузок. Отсюда следует, что основным критерием надежности сварных МК, например, трубопроводов и резервуаров, является их напряженно-деформированное состояние (НДС), которое во многом определяет их фактическую работоспособность к остяточный ресурс Поэтому актуальной задачей является разработка инженерных методик, которые позволяли бы оперативно определять и оценивать с приемлемой точностью поля напряжений и деформаций в конструкциях на различных стадиях деформирования [1].

Анализ показал, что напряженно-деформированное состояние, износ, накопление повреждений, разрушение деталей и узлов имеют особое закономерное проявление применительно только к конкретному виду нефтегазопромыслового оборудования и их нельзя автоматически использовать для целей анализа оборудования другого вида.

Система имеет две степени свободы. Вертикальные смещения точек соединения обозначаются через QiL и Q2L, как показано на рисунке, так что общее деформированное состояние системы может быть полностью описано безразмерными обобщенными координатами Qi и Q2. Обе они равны нулю в недеформированном состоянии системы.

Осуществлено методическое обеспечение эксплуатационной технологичности конструкций печей и топки в ТС СП, позволяющее стабилизировать напряженно-деформированное состояние и температурные поля КСП при эксплуатации.

При составлении условий равновесия реального тела оно может считаться абслютно твердым.

В действительности при нагружении форма и размеры тела меняются, поэтому точки приложения сил и линии их действия тоже меняются; учет этих изменений дает поправку в четвертом-пятом знаках численного результата, что несущественно.