19.) Абсолютная и относительная погрешности

19. любое измерение дает лишь приближенное значение физической величины, однако можно указать интервал, который содержит ее истинное значение:

  А_пр- DА < А_ист < А_пр+ DА

            Величина DА называется абсолютной погрешностью измерения величины А. Абсолютная погрешность выражается в единицах измеряемой величины. Абсолютная погрешность равна модулю максимально возможного отклонения значения физической величины от измеренного значения. А_пр- значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений.

         Но для оценки качества измерения необходимо определить относительную погрешность e. e= DА/А_пр или e= (DА/А_пр)*100%.

         Если при измерении получена относительная погрешность более 10%, то говорят, что произведена лишь оценка измеряемой величины. В лабораториях физического практикума рекомендуется проводить измерения с относительной погрешностью до 10%. В научных лабораториях некоторые точные измерения (например определение длины световой волны), выполняются с точностью миллионных долей процента.          Окончательный результат измерения физической величины А следует записывать в такой форме;

 

         А=А_пр+ D А,  e= (DА/А_пр)*100%.

А_пр- значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений. D А- полная абсолютная погрешность прямого измерения.          При обработке результатов косвенных измерений физической величины, связанной функционально с физическими величинами А, В и С, которые измеряются прямым способом, сначала определяют относительную погрешность косвенного измерения e= DХ/Х_пр, пользуясь формулами, приведенными в таблице (без доказательств).

         Абсолютную погрешность определяется по формуле DХ=Х_пр *e,

где e выражается десятичной дробью, а не в процентах.

         Окончательный результат записывается так же, как и в случае прямых измерений

20.) факторная и остаточная дисперсия

21.) дискретные и непрерывные временные ряды,их характеристики

21.Дискретные и непрерывные временные ряды,их характеристики.Уравнение тренда.Сглаживание временных рядов:метод скользящего среднего.

Последовательность результатов наблюдений над некоторой величиной полученных последовательно во времени,наз.- временным рядом.Например:последовательность значений температуры тела больного в течение суток если ее регистрацию проводили каждый час.

Величина случайного временного ряда в произвольный момент времени,может быть описана соответствующей функцией распределения и для такого ряда могут быть определеныосновные числовые характеристики,т.е. математическое ожидание,дисперсия и среднее квадратичное отклонение.В общем случае произвольного ряда эта функция распределения явл.функцией времени и такое ряд называют нестационарным.В то же время ряды,функция распределения значений которых не зависит от времени наз.- стационарным.Стационарные:их числовые характеристики не зависят от времени.

х1,х2….значение этого ряда полученных последовательно в течение некоторого периода наблюдения.

n-кол-во экспериментальных значений.

На практике часто возникает необходимость выявления основной тенденции изменения временного ряда(наз.- трендом)т.е. нахождения функции f(t)=at+b,где а,b коэффициенты.которые можно определить используя метод наименьших квадратов.

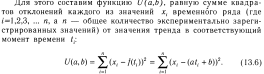
Сглаживание- дисперсия ряда уменьшается и он становится более плавным.Выбирают некоторый временной нтервал усреднения который как правило значительно меньше всего времени наблюдения за значениями врем. ряда,и с помощью этого интервала скользят вдоль ряда производя усреднение значений ряда,попадающих в этот скользящий

интервал.

22.) статистические гипотезы.Нулевая и конкурирующая гипотезы.Параметрический критерий Стьюденса. Пусть в (статистическом) эксперименте доступна наблюдению случайная величина , распределение которой  известно полностью или частично. Тогда любое утверждение,

касающееся  называется статистической гипотезой.

Если вид распределения или функция распределения выборки нам заданы, то в этом случае задача оценки различий двух групп независимых наблюдений может решаться с использованием параметрических критериев статистики: либо кри­терия Стьюдента (t), если сравнение выборок ведется по сред­ним значениям (X и У). В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.

Вычисление значения t осуществляется по формуле:

                                                                                                       (5)

  где  — разности между соответствующими значениями переменной X и переменной У, а d - среднее этих разностей;Sd вычисляется по следующей формуле:

                                                                                       (6)

Число степеней свободы k определяется по формуле k=n-1.

23.) статистические гипотезы

23) .Статисстические гипотезы. Пусть в (статистическом) эксперименте доступна наблюдению случайная величина , распределение которой  известно полностью или частично. Тогда любое утверждение, касающееся  называется статистической гипотезой. Статистическая гипотеза, однозначно определяющая распределение , то есть , где  какой-то конкретный закон, называется простой.Статистическая гипотеза, утверждающая принадлежность распределения  к некоторому семейству распределений, то есть вида , где  — семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза , называемая конкурирующей. Для преодоления указанных трудностей в практике педагоги­ческих исследований следует использовать непараметрические критерии статистики, такие, как критерий знаков, двухвыборочный критерий Вилкоксона, критерий Ван дер Вардена, критерий Спирмена, выбор которых, хотя и не требует большого числа членов выборки и знаний, вида распределения, но все же зависит от целого ряда условий.

24.) коэффициент корреляции и коэффициент частной корреляции 

24)  корреляционная зависимость — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.^[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение ^[2], либо коэффициент корреляции  (или )^[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.