11.) общие понятия теории вероятности и математической статистики

11. Математическая наука, изучающая общие закономерности случаайных явлений независимо от их конкретной природы и дающая методы количественной оценки называется теорией вероятности.

Математической статистикой называется наука, которая занимается разработкой методов описания и обработкой опытных данных с целью получения изучения закономерностей случайных массовых явлений.

Случайное событие – событие, которое в данных условиях может произойти, а может не произойти

Совместимые события – это события, для которых наступление одного из них не исключает возможности наступления других в данном испытании, т.е. они могут появиться вместе.

Несовместимые события - это события, для которых наступления одного из них исключает наступление других в одном и том же испытании, т.е. они не могут появиться вместе.

Случайной величиной, называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств.

Случайная величина называется дискретной, если она принимает счетное множество значений: число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека и т. д. Непрерывная случайная величина принимает любые значения внутри некоторого интервала: температура воздуха за определенный промежуток времени, масса зерен в колосьях пшеницы, координата места попадания пули в цель( принимаем пулю за материальную точку) и т. д.

Частота и относительная частота случайного события.

Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу испытаний.

Рассмотрим эксперименты с подбрасыванием монеты, при которых подсчитывается n- число подбрасываний и f – число выпадений «орла». Число f- называют частотой события «выпал орел», а число «f/n – относительной частотой этого события. Опыт показывает, что при увеличении числа экспериментов (n) относительная частота появления «орла» все более и более приближается к числу ½, которое называется вероятностью рассматриваемого события.

Вероя́тность — численная мера возможности наступления некоторого события.

Статистическое определение вероятности: Вероятностью случайного события А называется число Р(А), к которому приближается относительная частота этого события в длинной серии экспериментов.

Классическое определение вероятности: Вероятностью случайного события А называется отношение числа благоприятных для него исходов к числу всех равновозможных исходов. Р(А) = m/n (орёл-решка, кубики и т. п.)

12.) теорема сложения для несовместных событий

12. Теорема сложения: вероятность появления какого-либо события из нескольких несовместных равна сумме их вероятностей. P(A или B)=P(A)+P(B)..

Теорема умножения: вероятность совместного появления независимых событий равна произведению их вероятностей. P(A и B)=P(A)*P(B).

Условная вероятность – вероятность некоторого события при условии того, что другое событие произошло, либо не произошло. Например, событие А произойдет при условии реализации события В. В таком случае используют обозначение Р(А/В).

Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий, то вероятность события Авычисляется по формуле

Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H₁, H₂, ..., H_n, образующих полную группу. Тогда вероятность события A определяется как сумма произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:

Эта формула называется формулой полной вероятности.

Формула Бейеса (Байеса)

Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H₁, H₂, ..., H_n, образующих полную группу. Событие A уже произошло. Требуется вычислить условные вероятности гипотез (при условии, что событие А произошло).

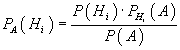
13.) дискретные и непрерывные случайные величины

13. Случайная величина называется дискретной, если она принимает счетное множество значений: число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека и т. д. Непрерывная случайная величина принимает любые значения внутри некоторого интервала: температура воздуха за определенный промежуток времени, масса зерен в колосьях пшеницы, координата места попадания пули в цель( принимаем пулю за материальную точку) и т. д.

Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случайных величин оно определяется, как сумма произведений случайной величины на вероятность ее появления:

Свойства математического ожидания

1.M(C)=C,

2.M(CX)=CM(X).

3.M(X+Y)= M(X)+M(Y),

4.M(X×Y)= M(X)M(Y), если X и Y – независимые C.B.

Дисперсия описывает разброс случайных величин относительно математического ожидания. Дисперсия дискретных случайных величин определяется, как сумма произведений квадратов разности случайных величин и математического ожидания на соответствующие вероятности появления этих случайных величин:

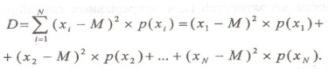
1. Свойства дисперсии

1.D(C)=0,

2.D(CX)= C²D(X).

3.D(X+Y)= D(X)+D(Y),если X и Y – независимые с.в.

14.) Функции распределения вероятностей появления дискретных случайных величин

14. Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x: F(X)=P(ξ<X). Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного.

Формула Бернулли

Пусть проводятся независимые испытания (такие, при которых вероятность появления события в каждом испытании не зависит от результатов предыдущих испытаний). Далее, вероятность наступления интересующего нас события в каждом испытании постоянна и равна p. Тогда вероятность того, что рассматриваемое событие появится ровно k раз при n испытаниях (безразлично, в каком порядке), равна

Пример 1

Система, составленная из четырёх блоков, работает исправно, если за рассматриваемый период выйдет из строя не более двух блоков. Найти вероятность безотказной работы системы блоков, если отказы блоков являются независимыми событиями и вероятность отказа каждого блока равна 1/8.

Решение Вероятность того, что за рассматриваемый период ни один из блоков не выйдет из строя:

Вероятность того, что за рассматриваемый период выйдет из строя один блок:

Вероятность того, что за рассматриваемый период выйдет из строя два блока:

Вероятность безотказной работы системы:

Формула Пуассона

Если при наличии схемы Бернулли число испытаний n велико, а вероятность наступления события p мала, то вместо формулы Бернулли используют формулу Пуассона:

Пример 2

Вероятность выпуска бракованного сверла (повышенной хрупкости) равна 0,02. Свёрла укладывают в коробки по 100 штук. Определить вероятность того, что число бракованных свёрл коробке не превосходит трёх.

Решение Так же, как и в предыдущей задаче, здесь имеется схема Бернулли. n = 100, p = 0,02; q = 0,98. Вероятность наступления события мала, количество производимых испытаний велико (np < 9). Используем приближённую формулу Пуассона.

15.) числовые характеристики непрерывной случайной величины

15. Математическое ожидание: для непрерывных случайных величин - это операция интегрирования математич.ожидания для дискретных величин:

Дисперсия для непрерывных случайных величин:

Среднее квадратическое отклонение, как и у дискретных:

СВ распределена по этому закону, если плотность вероятности имеет вид

a=M(X) – мат.ожидание СВ, σ – среднее квадратическое отклонение, σ²- дисперсия СВ

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ - стандартное отклонение (σ² —дисперсия) распределения.

Критерии, основанные на нормальном распределении Сравнение выборочного среднего арифметического со средним значением генеральной совокупности

Рассмотрим, как с помощью статистических критериев решить вопрос: значимо ли отличие выборочного среднего значения от среднего значения генеральной совокупности, из которой предположительно взята выборка, или наблюдаемое различие является случайным? Такая постановка вопроса типична для выборочного контроля качества продукции в промышленности, но и при исследованиях в правоведении такой вопрос часто возникает, когда предстоит решить, значимо ли отличается среднее значение признака, полученное по выборке, от среднего значения, известного по результатам многочисленных предыдущих экспериментов.

Применяемый для этих целей t-критерий Стьюдента основан на предположении о нормальности распределения генеральной совокупности, но результаты проверки гипотез удовлетворяют по точности и при небольших отклонениях от нормальности распределения.

Условия применения t-критерия: выборка получена из генеральной совокупности, имеющей приближенно нормальное распределение с параметрами  и .

Гипотеза Н₀:  =  – среднее значение  генеральной совокупности, из которой получена выборка, равно данному значению  (известному, например, из предыдущих экспериментов).

Альтернатива Н₀:  (двусторонний критерий применяется тогда, когда допускаются отклонения в обе стороны от ).

Уровень значимости:.

Порядок применения T-критерия:

1. Принимается предположение о нормальности, формулируются гипотезы Н₀ и H₁ задается уровень значимости .

2. Получают выборку объема n.

3. Вычисляется выборочное среднее арифметическое  и исправленная выборочная дисперсия S².

4. Определяется значение t-критерия по формуле:

                                                                                                                              (6.1)

Величина t имеет при справедливости гипотезы Н₀ t-распределение Стьюдента (определенное в гл. 4) с =n–1 степенями свободы.

5. По таблицам находится t_критич – критическое значение t-критерия при уровне значимости  и числе степеней свободы =n–1. (Таблицы обычно содержит критические значения t_критич для двустороннего критерия.)

6. Делается вывод: если , то выборочное среднее значимо отличается от  на уровне значимости , и в этой ситуации отклоняется гипотеза Н₀, т. е. считается, что выборка взята из другой генеральной совокупности, для которой . Если , то на заданном уровне различие незначимо и сохраняется гипотеза Н₀.