11. Математическая наука, изучающая общие закономерности случаайных явлений независимо от их конкретной природы и дающая методы количественной оценки называется теорией вероятности.

Математической статистикой называется наука, которая занимается разработкой методов описания и обработкой опытных данных с целью получения изучения закономерностей случайных массовых явлений.

Случайное событие – событие, которое в данных условиях может произойти, а может не произойти

Совместимые события – это события, для которых наступление одного из них не исключает возможности наступления других в данном испытании, т.е. они могут появиться вместе.

Несовместимые события - это события, для которых наступления одного из них исключает наступление других в одном и том же испытании, т.е. они не могут появиться вместе.

Случайной величиной, называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств.

Случайная величина называется дискретной, если она принимает счетное множество значений: число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека и т. д. Непрерывная случайная величина принимает любые значения внутри некоторого интервала: температура воздуха за определенный промежуток времени, масса зерен в колосьях пшеницы, координата места попадания пули в цель( принимаем пулю за материальную точку) и т. д.

Частота и относительная частота случайного события.

Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу испытаний.

Рассмотрим эксперименты с подбрасыванием монеты, при которых подсчитывается n- число подбрасываний и f – число выпадений «орла». Число f- называют частотой события «выпал орел», а число «f/n – относительной частотой этого события. Опыт показывает, что при увеличении числа экспериментов (n) относительная частота появления «орла» все более и более приближается к числу ½, которое называется вероятностью рассматриваемого события.

Вероя́тность — численная мера возможности наступления некоторого события.

Статистическое определение вероятности: Вероятностью случайного события А называется число Р(А), к которому приближается относительная частота этого события в длинной серии экспериментов.

Классическое определение вероятности: Вероятностью случайного события А называется отношение числа благоприятных для него исходов к числу всех равновозможных исходов. Р(А) = m/n (орёл-решка, кубики и т. п.)

12. Теорема сложения: вероятность появления какого-либо события из нескольких несовместных равна сумме их вероятностей. P(A или B)=P(A)+P(B)..

Теорема умножения: вероятность совместного появления независимых событий равна произведению их вероятностей. P(A и B)=P(A)*P(B).

Условная вероятность – вероятность некоторого события при условии того, что другое событие произошло, либо не произошло. Например, событие А произойдет при условии реализации события В. В таком случае используют обозначение Р(А/В).

Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий, то вероятность события Авычисляется по формуле

Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H1, H2, ..., Hn, образующих полную группу. Тогда вероятность события A определяется как сумма произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:

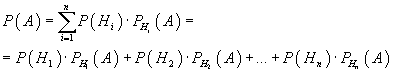
Эта формула называется формулой полной вероятности.

Формула Бейеса (Байеса)

Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H1, H2, ..., Hn, образующих полную группу. Событие A уже произошло. Требуется вычислить условные вероятности гипотез (при условии, что событие А произошло).

13. Случайная величина называется дискретной, если она принимает счетное множество значений: число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека и т. д. Непрерывная случайная величина принимает любые значения внутри некоторого интервала: температура воздуха за определенный промежуток времени, масса зерен в колосьях пшеницы, координата места попадания пули в цель( принимаем пулю за материальную точку) и т. д.

Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случайных величин оно определяется, как сумма произведений случайной величины на вероятность ее появления:

Свойства математического ожидания

1.M(C)=C,

2.M(CX)=CM(X).

3.M(X+Y)= M(X)+M(Y),

4.M(X×Y)= M(X)M(Y), если X и Y – независимые C.B.

Дисперсия описывает разброс случайных величин относительно математического ожидания. Дисперсия дискретных случайных величин определяется, как сумма произведений квадратов разности случайных величин и математического ожидания на соответствующие вероятности появления этих случайных величин:

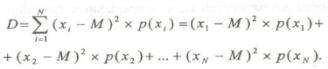
1. Свойства дисперсии

1.D(C)=0,

2.D(CX)= C²D(X).

3.D(X+Y)= D(X)+D(Y),если X и Y – независимые с.в.

14. Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x: F(X)=P(ξ<X). Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного.

 Формула Бернулли

Пусть проводятся независимые испытания (такие, при которых вероятность появления события в каждом испытании не зависит от результатов предыдущих испытаний). Далее, вероятность наступления интересующего нас события в каждом испытании постоянна и равна p. Тогда вероятность того, что рассматриваемое событие появится ровно k раз при n испытаниях (безразлично, в каком порядке), равна

Пример 1

Система, составленная из четырёх блоков, работает исправно, если за рассматриваемый период выйдет из строя не более двух блоков. Найти вероятность безотказной работы системы блоков, если отказы блоков являются независимыми событиями и вероятность отказа каждого блока равна 1/8.

Решение Вероятность того, что за рассматриваемый период ни один из блоков не выйдет из строя:

Вероятность того, что за рассматриваемый период выйдет из строя один блок:

Вероятность того, что за рассматриваемый период выйдет из строя два блока:

Вероятность безотказной работы системы:

формула Пуассона

Если при наличии схемы Бернулли число испытаний n велико, а вероятность наступления события p мала, то вместо формулы Бернулли используют формулу Пуассона:

Пример 2

Вероятность выпуска бракованного сверла (повышенной хрупкости) равна 0,02. Свёрла укладывают в коробки по 100 штук. Определить вероятность того, что число бракованных свёрл коробке не превосходит трёх.

Решение Так же, как и в предыдущей задаче, здесь имеется схема Бернулли. n = 100, p = 0,02; q = 0,98. Вероятность наступления события мала, количество производимых испытаний велико (np < 9). Используем приближённую формулу Пуассона.

15. Математическое ожидание: для непрерывных случайных величин - это операция интегрирования математич.ожидания для дискретных величин:

Дисперсия для непрерывных случайных величин:

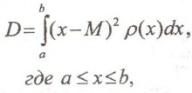
Среднее квадратическое отклонение, как и у дискретных:

СВ распределена по этому закону, если плотность вероятности имеет вид

a=M(X) – мат.ожидание СВ, σ – среднее квадратическое отклонение, σ²- дисперсия СВ

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ - стандартное отклонение (σ² —дисперсия) распределения.

Критерии, основанные на нормальном распределении Сравнение выборочного среднего арифметического со средним значением генеральной совокупности

Рассмотрим, как с помощью статистических критериев решить вопрос: значимо ли отличие выборочного среднего значения от среднего значения генеральной совокупности, из которой предположительно взята выборка, или наблюдаемое различие является случайным? Такая постановка вопроса типична для выборочного контроля качества продукции в промышленности, но и при исследованиях в правоведении такой вопрос часто возникает, когда предстоит решить, значимо ли отличается среднее значение признака, полученное по выборке, от среднего значения, известного по результатам многочисленных предыдущих экспериментов.

Применяемый для этих целей t-критерий Стьюдента основан на предположении о нормальности распределения генеральной совокупности, но результаты проверки гипотез удовлетворяют по точности и при небольших отклонениях от нормальности распределения.

Условия применения t-критерия: выборка получена из генеральной совокупности, имеющей приближенно нормальное распределение с параметрами  и .

Гипотеза Н₀:  =  – среднее значение  генеральной совокупности, из которой получена выборка, равно данному значению  (известному, например, из предыдущих экспериментов).

Альтернатива Н₀:  (двусторонний критерий применяется тогда, когда допускаются отклонения в обе стороны от ).

Уровень значимости:.

Порядок применения T-критерия:

1. Принимается предположение о нормальности, формулируются гипотезы Н₀ и H₁ задается уровень значимости .

2. Получают выборку объема n.

3. Вычисляется выборочное среднее арифметическое  и исправленная выборочная дисперсия S².

4. Определяется значение t-критерия по формуле:

                                                                                                                              (6.1)

Величина t имеет при справедливости гипотезы Н₀ t-распределение Стьюдента (определенное в гл. 4) с =n–1 степенями свободы.

5. По таблицам находится t_критич – критическое значение t-критерия при уровне значимости  и числе степеней свободы =n–1. (Таблицы обычно содержит критические значения t_критич для двустороннего критерия.)

6. Делается вывод: если , то выборочное среднее значимо отличается от  на уровне значимости , и в этой ситуации отклоняется гипотеза Н₀, т. е. считается, что выборка взята из другой генеральной совокупности, для которой . Если , то на заданном уровне различие незначимо и сохраняется гипотеза Н₀.

16. Стандартный интервал а</=х</=b

Вероятность попадания в него случайной величины

Р(а</=х</=b)= ар (плотность) (Х)dx

Доверительная вероятность α – некоторая заданная вероятность, с которой случ.величина попадает в определённый интервал.

Такой интервал – доверительный. Стандартные интервалы

(вместо < должно быть </=)

1. М- σ <х< М+ σ (α = 68%)

2. М- 2σ <х< М+ 2σ (α = 95%)

3. М- 3σ <х< М+ 3σ (α = 99,7%)

Доверительный интервал в математической статистике - это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой что он содержит этот параметр с заданной вероятностью.

Определение

Пусть есть выборка из распределения , где - неизвестный параметр. Пусть также задана . Тогда случайный интервал , где

есть некоторые статистики имеющейся выборки, такой что

,

называется -доверительным интервалом для параметра .

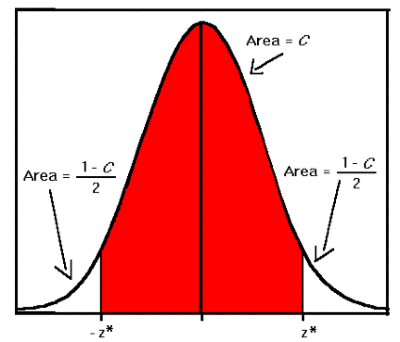(доверительный интервал для нормального распределение)

17. Генеральной совокупностью называют совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений случайной величины, или совокупность результатов всех мыслимых наблюдений,  проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов.

Замечание: Часто генеральная совокупность содержит конечное число объектов. Однако если это число достаточно велико, то иногда в целях упрощения вычислений допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки. Выборочной совокупностью называют часть отобранных объектов из генеральной совокупности.

( Генеральная средняя. Пусть изучается генеральная совокупность относительно количественного признака Х. Генеральной средней называют среднее арифметическое значений признака генеральной совокупности. Если все значения признака различны, то Если значения признака имеют частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то

.Выборочная средняя. Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n. Выборочной средней называют среднее арифметическое значение признака выборочной совокупности. Если все значения признака выборки различны, то если же все значения имеют частоты n1, n2,…,nk, то

Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней. )

Число наблюдений, образующих выборку, называется объемом выборки.

Репрезентативности выборки - полнота и адекватность свойств генеральной совокупности, по отношению к которой эту выборку можно считать представительной.

Точечная и интервальная оценка параметра генеральной совокупности. Предположим, что по выборке нужно найти не интервал, в котором находится параметр, а одно число которое ближе всего к параметру. Под оценкой понимается любое число, рассчитанное по выборке и характеризующее параметр.Свойства точечной оценки: Несмещенность – среднее выборочного распределения оценки равно величине параметра. Состоятельность – при увеличении объема выборки оценка приближается к значения измеряемого параметра. Эффективность – чем ниже дисперсия, т.е. чем меньше отличаются оценки, полученные в разных выборках, тем выше эффективность.

Средняя арифметическая - такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Для того чтобы вычислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число.Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примером средней арифметической может служить общий фонд заработной платы — это сумма заработных плат всех работников.

Средняя арифметическая может быть вычислена по формуле:

где n — численность совокупности.

Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.

• X_Me  -нижняя граница медианного интервала

• h_Me   -величина медианного интервала;

• S_Me-1-сумма накопленных частот интервала, предшествующего медианному интервалу;

• f_Me  -локальная частота медианного интервала.

Мода (Mo) − величина, наиболее часто встречающаяся в данной совокупности. В вариационном ряду это − варианта, имеющая наибольшую частоту. Медианой (Me) называют варианту, которая является серединой упорядоченного (ранжированного) вариационного ряда, т. е. делит его на две равные части: одна часть имеет значения вариационного признака, меньшие средней, другая − бóльшие. Медиана указывает на значение вариационного признака, которого достигла половина единиц совокупности.

Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения. Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда.

• _ХМ0 — нижняя граница модального интервала;

• h_Mo  - величина (шаг, ширина) модального интервала;

• f₁ - локальная частота интервала, предшествующего модальному;

• f₂ - локальная частота модального интервала;

• f₃ - локальная частота интервала, следующего за модальным.

Модальный интервал определяется по наибольшей частоте.

18. Размах вариации — это разность между максимальным и минимальным значениями признака

Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.

Среднее абсолютное отклонение (mean absolute deviation) =арифметическое среднее отклонений всех значений от среднего. Абсолютным оно является потому, что суммируются отклонения по модулю, так как в противном случае сумма всех разбросов была бы равна нулю. Формула среднего абсолютного отклонения:    Выборочная дисперсия в математической статистике — это оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию и несмещённую, или исправленную, выборочные дисперсии. ,

где символ  обозначает выборочное среднее.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно  

  Для исправления выборочной дисперсии достаточно умножить ее на дробь

получим исправленную дисперсию S². Исправленная дисперсия является несмещенной оценкой.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение.

19. любое измерение дает лишь приближенное значение физической величины, однако можно указать интервал, который содержит ее истинное значение:

  А_пр- DА < А_ист < А_пр+ DА

            Величина DА называется абсолютной погрешностью измерения величины А. Абсолютная погрешность выражается в единицах измеряемой величины. Абсолютная погрешность равна модулю максимально возможного отклонения значения физической величины от измеренного значения. А_пр- значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений.

         Но для оценки качества измерения необходимо определить относительную погрешность e. e= DА/А_пр или e= (DА/А_пр)*100%.

         Если при измерении получена относительная погрешность более 10%, то говорят, что произведена лишь оценка измеряемой величины. В лабораториях физического практикума рекомендуется проводить измерения с относительной погрешностью до 10%. В научных лабораториях некоторые точные измерения (например определение длины световой волны), выполняются с точностью миллионных долей процента.          Окончательный результат измерения физической величины А следует записывать в такой форме;

 

         А=А_пр+ D А,  e= (DА/А_пр)*100%.

А_пр- значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений. D А- полная абсолютная погрешность прямого измерения.          При обработке результатов косвенных измерений физической величины, связанной функционально с физическими величинами А, В и С, которые измеряются прямым способом, сначала определяют относительную погрешность косвенного измерения e= DХ/Х_пр, пользуясь формулами, приведенными в таблице (без доказательств).

         Абсолютную погрешность определяется по формуле DХ=Х_пр *e,

где e выражается десятичной дробью, а не в процентах.

         Окончательный результат записывается так же, как и в случае прямых измерений

20.Дисперсионный анализ — это статистический метод оценки связи между факторными и результативным признаками в различных группах, отобранный случайным образом, основанный на определении различий (разнообразия) значений признаков. В основе дисперсионного анализа лежит анализ отклонений всех единиц исследуемой совокупности от среднего арифметического. В качестве меры отклонений берется дисперсия (В)— средний квадрат отклонений. Отклонения, вызываемые воздействием факторного признака (фактора) сравниваются с величиной отклонений, вызываемых случайными обстоятельствами. Если отклонения, вызываемые факторным признаком, более существенны, чем случайные отклонения, то считается, что фактор оказывает существенное влияние на результативный признак.

Doбщ. = Dфакт + D ост.,

Doбщ. - общая дисперсия наблюдаемых значений (вариант), характеризуется разбросом вариант от общего среднего. Измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Общее разнообразие складывается из межгруппового и внутригруппового;

Dфакт - факторная (межгрупповая) дисперсия, характеризуется различием средних в каждой группе и зависит от влияния исследуемого фактора, по которому дифференцируется каждая группа. Например, в группах различных по этиологическому фактору клинического течения пневмонии средний уровень проведенного койко-дня неодинаков — наблюдается межгрупповое разнообразие.

D ост. - остаточная (внутригрупповая) дисперсия, которая характеризует рассеяние вариант внутри групп. Отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неуточненных факторов и не зависящую от признака — фактора, положенного в основание группировки. Вариация изучаемого признака зависит от силы влияния каких-то неучтенных случайных факторов, как от организованных (заданных исследователем), так и от случайных (неизвестных) факторов.

Однофакторный дисперсионный анализ

Задачей дисперсионного анализа является изучение влияния одного или нескольких факторов на рассматриваемый признак.

Однофакторный дисперсионный анализ используется в тех случаях, когда есть в распоряжении три или более независимые выборки, полученные из одной генеральной совокупности путем изменения какого-либо независимого фактора, для которого по каким-либо причинам нет количественных измерений.

Для этих выборок предполагают, что они имеют разные выборочные средние и одинаковые выборочные дисперсии. Поэтому необходимо ответить на вопрос, оказал ли этот фактор существенное влияние на разброс выборочных средних или разброс является следствием случайностей, вызванных небольшими объемами выборок. Другими словами если выборки принадлежат одной и той же генеральной совокупности, то разброс данных между выборками (между группами) должен быть не больше, чем разброс данных внутри этих выборок (внутри групп).

Пусть Xik – i – элемент (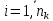)k -выборки ( ), где m – число выборок,– число данных вk -выборке. Тогда – выборочное среднееk - выборки определяется по формуле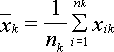

Общее среднее вычисляется по формуле

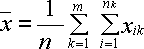 , где  

Основное тождество дисперсионного анализа имеет следующий вид:

 , где Q1 – сумма квадратов отклонений выборочных средних от общего среднего(сумма квадратов отклонений между группами); Q2 – сумма квадратов отклонений наблюдаемых значенийот выборочной средней(сумма квадратов отклонений внутри групп); Q – общая сумма квадратов отклонений наблюдаемых значенийот общего среднего.

Расчет этих сумм квадратов отклонений осуществляется по следующим формулам:

 

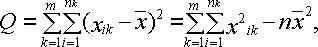
В качестве критерия необходимо воспользоваться критерием Фишера:

 

.

Если расчетное значение критерия Фишера будет меньше, чем табличное значение – нет оснований считать, что независимый фактор оказывает влияние на разброс средних значений, в противном случае, независимый фактор оказывает существенное влияние на разброс средних значений (λ– уровень значимости, уровень риска, обычно для экономических задач λ=0,05).

Недостаток однофакторного анализа: невозможно выделить те выборки, которые отличаются от других. Для этой цели необходимо использовать метод Шеффе или проводить парные сравнения выборок.

• Двухфакторный анализ с повторением. Расширенный дисперсионный анализ с несколькими выборками (или повторениями) для каждой группы данных.

• Двухфакторный анализ без повторений. Расширенный дисперсионный анализ с одной выборкой для каждой группы данных.

• При определении влияния на зависимую переменную нескольких факторов можно использовать многофакторный дисперсионный анализ. Главное преимущество этого метода в том, что он позволяет исследователю изучать взаимодействие факторов. Взаимодействия (interaction) имеют место, когда эффекты одного фактора на зависимую переменную зависят от уровня других факторов.

• Процедура многофакторного дисперсионного анализа аналогична процедуре однофакторного дисперсионного анализа. Статистики, соответствующие многофакторному дисперсионному анализу, также определяются аналогично определению статистик в однофакторном дисперсионном анализе.

21.Дискретные и непрерывные временные ряды,их характеристики.Уравнение тренда.Сглаживание временных рядов:метод скользящего среднего.

Последовательность результатов наблюдений над некоторой величиной полученных последовательно во времени,наз.- временным рядом.Например:последовательность значений температуры тела больного в течение суток если ее регистрацию проводили каждый час.

Величина случайного временного ряда в произвольный момент времени,может быть описана соответствующей функцией распределения и для такого ряда могут быть определеныосновные числовые характеристики,т.е. математическое ожидание,дисперсия и среднее квадратичное отклонение.В общем случае произвольного ряда эта функция распределения явл.функцией времени и такое ряд называют нестационарным.В то же время ряды,функция распределения значений которых не зависит от времени наз.- стационарным.Стационарные:их числовые характеристики не зависят от времени.

х1,х2….значение этого ряда полученных последовательно в течение некоторого периода наблюдения.

n-кол-во экспериментальных значений.

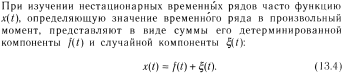На практике часто возникает необходимость выявления основной тенденции изменения временного ряда(наз.- трендом)т.е. нахождения функции f(t)=at+b,где а,b коэффициенты.которые можно определить используя метод наименьших квадратов.

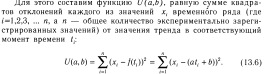
Сглаживание- дисперсия ряда уменьшается и он становится более плавным.Выбирают некоторый временной нтервал усреднения который как правило значительно меньше всего времени наблюдения за значениями врем. ряда,и с помощью этого интервала скользят вдоль ряда производя усреднение значений ряда,попадающих в этот скользящий

интервал.

22)Статистические гипотезы.Нулевая и конкурирующая гипотезы.Параметрический критерий Стьюденса. Пусть в (статистическом) эксперименте доступна наблюдению случайная величина , распределение которой известно полностью или частично. Тогда любое утверждение, касающееся называется статистической гипотезой.

Если вид распределения или функция распределения выборки нам заданы, то в этом случае задача оценки различий двух групп независимых наблюдений может решаться с использованием параметрических критериев статистики: либо кри­терия Стьюдента (t), если сравнение выборок ведется по сред­ним значениям (X и У). В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.

Вычисление значения t осуществляется по формуле:

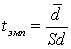                                                                                                       где — разности между соответствующими значениями переменной X и переменной У, а d - среднее этих разностей;Sd вычисляется по следующей формуле:

                                                                    Число степеней свободы k определяется по формуле k=n-1.

23) .Статисстические гипотезы. Пусть в (статистическом) эксперименте доступна наблюдению случайная величина , распределение которой известно полностью или частично. Тогда любое утверждение, касающееся называется статистической гипотезой. Статистическая гипотеза, однозначно определяющая распределение , то есть , где какой-то конкретный закон, называется простой.Статистическая гипотеза, утверждающая принадлежность распределения к некоторому семейству распределений, то есть вида , где  — семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза , называемая конкурирующей. Для преодоления указанных трудностей в практике педагоги­ческих исследований следует использовать непараметрические критерии статистики, такие, как критерий знаков, двухвыборочный критерий Вилкоксона, критерий Ван дер Вардена, критерий Спирмена, выбор которых, хотя и не требует большого числа членов выборки и знаний, вида распределения, но все же зависит от целого ряда условий.

24)  корреляционная зависимость — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.^[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение ^[2], либо коэффициент корреляции (или )^[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.

25)Линии регрессии. Пусть и - две случайные непрерывные величины, находящиеся в корреляционной зависимости. Это значит, что каждому значению x случайной величины соответствует вполне определенное распределение вероятностей величины . Плотность распределения величины при условии, что , называется условной плотностью распределенияслучайной величины .     Вычислим для данного случая так называемое условное математическое ожидание величины при условии, что . Согласно определению математического ожидания непрерывной случайной величины, имеем

Каждому возможному значению x случайной величины соответствует определенное значение условного математического ожидания . Таким образом, мы получаем функцию переменной x. Эта функция y=f(x) называется функцией регрессии величины на , а ее график - линией регрессии на .  Аналогично определяется условное математическое ожидание величины при условии, что :

где - условная плотность вероятности случайной величины при условии, что .     Функция x=g(y) называется функцией регрессии величины на , а ее график - линией регрессии на 

Метод наименьших квадратов заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.