. Вторая экваториальная система координат

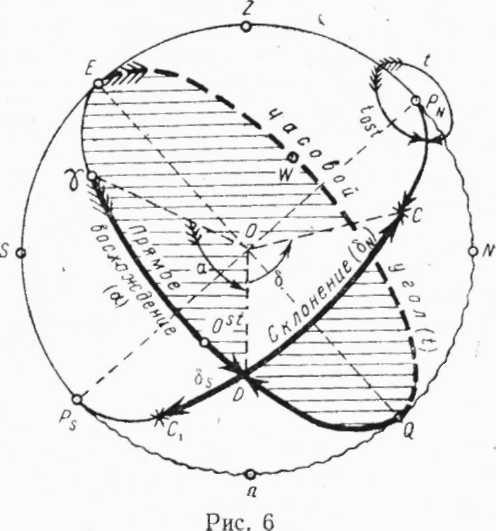
В этой системе основными кругами являются небесный экватор и меридиан точки весеннего равноденствия, которая обозначается зна­ком γ созвездия Овна.

Точка γ занимает на небесном экваторе совершенно определенное и независимое от наблюдателя положение, поэтому выбор меридиана этой точки за начало отсчета координат представляет значительные удобства, особенно при счете времени.

Положение светила в этой системе определяется двумя экватори­альными координатами: прямым восхождением и склонением

1) Прямым восхождением (а) светила называется дуга экватора от точки весеннего равноденствия (γ) до меридиана светила, считае­мая от 0 до 360° в сторону, обратную счету W-x часовых углов (в сто­рону, обратную суточному вращению сферы). Например, светило С имеет α =65°.

В современных отечественных и зарубежных пособиях (например, в морских астрономических ежегодниках) вместо прямого восхождения звезд употребляется так называемое звездное дополнение (τ), пред­ставляющее дополнение а до 360°, т. е.

τ == 360° — а.

Очевидно, что звездное дополнение т представляет собой дугу эк­ватора от точки γ до меридиана светила, считаемую в сторону W-х ча­совых углов.

Например, для светила C имеем α = 65°, τ = 295°.

Величину τ не принято считать специальной координатой, а лишь вспомогательной величиной, однако с ее введением для звезд необхо­димость в координате а отпадает. Прямое восхождение (или величина τ) определяет на сфере положение меридиана светила.

Второй координатой этой системы является склонение δ, рас­смотренное в первой экваториальной системе координат.

Таким образом, вторая экваториальная система отличается от пер­вой только положением исходного меридиана.

Для перехода от первой экваториальной системы ко второй, и на­оборот, необходимо знать только положение на экваторе точки γ, ко­торое в каждый момент времени определяется ее W-м часовым углом (на рис. дуга EWγ), обозначаемым tγ , Из рисунка видно, что дуга EWDравная W-му часовому углу светила С, и дуга γD равная его прямому восхождению, в сумме равны дуге EWγ, т. е. часовому углу точки Овна, следовательно:

^tγ ₌ ^{t +α}

По этой формуле можно переходить от координат первой эквато­риальной системы ко второй, если известна величина tγ.

В дальнейшем мы установим, что величиной tγ измеряется звезд­ное время, поэтому ее можно легко получить для любого момента по часам.

Заканчивая рассмотрение систем сферических координат, коснемся вопроса о единицах измерения координат.

Сферические координаты представляют собой дуги больших кру­гов, поэтому они могут измеряться в тех же мерах, в каких измеряются дуги и углы, т.е. в градусах и радианах. Для перехода от градусной меры в радианную применяется табл. 36 МТ-53 или общие правила .

Помимо этих мер, в астрономии применяется часовая мера дуг. В основу этих единиц положен промежуток времени в одни сут­ки, за который Земля совершает оборот на 360° и, следовательно, ок­ружность заключает 24 ч. Отсюда получаются соотношения: 24 ц = 360°; 1^Ч = 15°, 1* = 15'; 1^с = 15" = 0',25 или Г=4^Л; Г = 4^е и т. д. Правила пе­рехода от одних единиц к другим изложены далее.

В часовых единицах иногда измеряются величины α, t, tγ, а иног­да и географические долготы.

Например: α = 220° = 14^ч40^л; tγ = II0° = 7-20* и т. д.