Белорусский государственный университет

механико–математический факультет

Кафедра общей математики и информатики

Матейко О. М., Плащинский П.В.

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ВЫСШАЯ МАТЕМАТИКА

Часть 2

МИНСК

 Матейко О. М., Плащинский П.В., 2005.

§ 1. Интегральное исчисление функций

одной переменной

Перечень вопросов по теме

1. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла.

2. Таблица интегралов. Основные методы интегрирования: непосредственное интегрирование, метод подстановки, метод интегрирования по частям.

3. Интегрирование рациональных дробей с квадратным трехчленом в знаменателе.

4. Интегрирование иррациональных функций с квадратным трехчленом в знаменателе.

5. Интегрирование рациональных функций.

6. Интегрирование тригонометрических выражений.

7. Интегрирование иррациональных функций.

8. Определенный интеграл: определение, геометрический и физический смысл. Условия интегрируемости функций.

9. Свойства определенного интеграла. Теорема о среднем.

10. Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница.

11. Замена переменной в определенном интеграле. Формула интегрирования по частям.

12. Приложения определенного интеграла: вычисление площадей плоских фигур, длины дуги плоской кривой, объемов геометрических тел.

Задание 1. Вычислить указанные неопределенные интегралы.

		;		;
		;		;
		;		.

Решение варианта 0.

Пример 0.1. Непосредственным интегрированием получаем:

.

Пример 0.2. Аналогично,

.

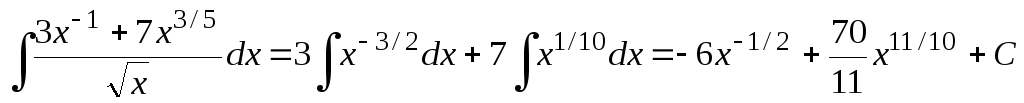Пример 0.3. Применяя формулу интегрирования по частям, имеем:

.

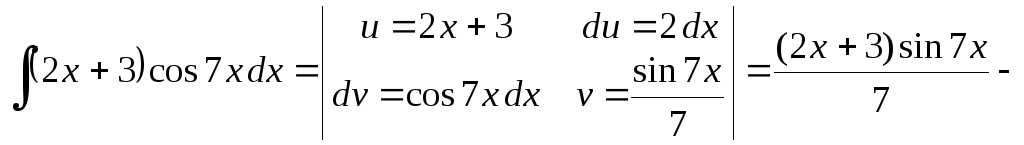
Пример 0.4. Применяя тригонометрические формулы понижения степени, приводим интегралы к табличному виду:

.

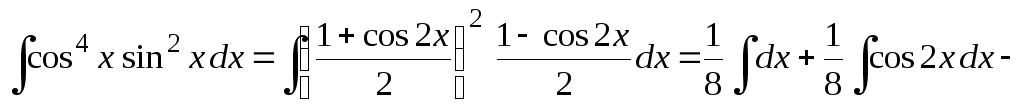
Пример 0.5. Выделяем в числителе производную знаменателя, а затем, выделяя в трехчлене полный квадрат, приводим интегралы к табличному виду:

.

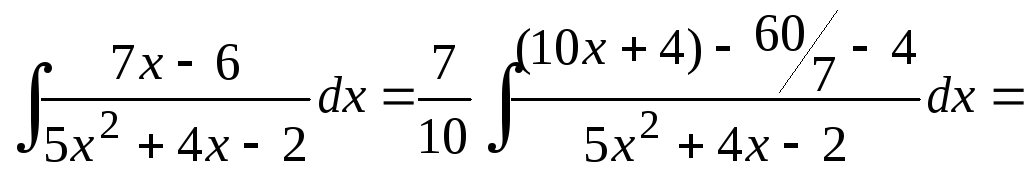
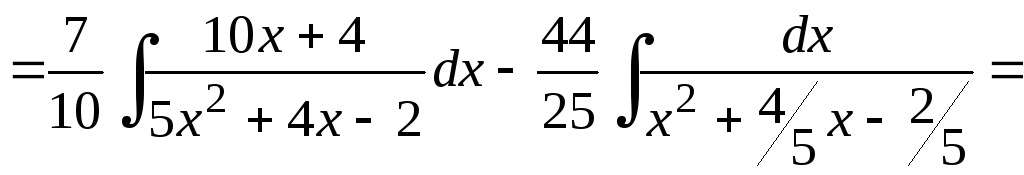
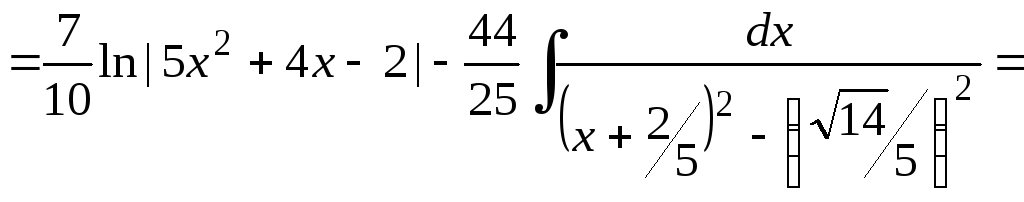
Пример 0.6. После степенной замены подынтегральная функция становится рациональной:

.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
				.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.

		;		;
		;		;
		;		.
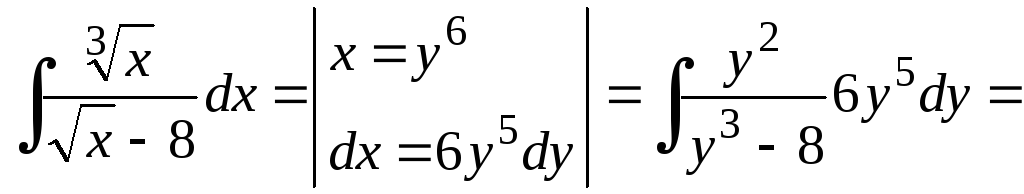