Добавил:

pmaxim2006 fizmathim.ru Решаю задачи по высшей математике. Фотографии решенных заданий по высшей математике https://fizmathim.ru/photo/ Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Павлодарский государственный университет им. С. Торайгырова

Предмет:

Математика

Файл:

ИДЗ 2.1 Рябушко пример решения

.pdf

Скачиваний:

499

Добавлен:

20.02.2017

Размер:

255.44 Кб

Скачать

☆

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

ИДЗ 2.1 – Вариант 0

1. Даны векторы a = αm+βn и b = γm+δn, где |m| = k; |n| = l; (m,^n) = φ. Найти а) (λa+μb)∙(νa+τb); б) прв(νa+τb); в) cos(a,^τb)

1.0 α = 3, β = –2, γ = 4, δ = 5,						k = 3, l = 2, φ = 5π/3, λ = 3, μ = 2, ν = 1, τ = 1
	m	3 ,	n	2		5 / 3

					, m, n

a 3m 2n					b 4m 5n

а) 3a 2b a b

Подставляем начальные данные, вычисляем

3a 3 3m 2n 9m 6n

2b 2 4m 5n 8m 10n

3a 2b 9m 8m 6n 10n 17m 4n

a3m 2n

b4m 5n

a b 3m 2n 4m 5n 7m 3n

В итоге:

3a 2b a b 17m 4n 7m 3n 119m																												2	79	m	n							12n			2
																												2													2
																																cos m, n
119 32						79 3 2 0,5 12 22												1071 237 48 1356
119 32						79 3 2 0,5 12 22												1071 237 48 1356
б) пр b a b
Пусть					c a b 7m 3n
Тогда					пр			c			c		b
							b					b




Найдем значения c b и																b	:
c b 7m									3n 4m					5n 28m						2	47		m		n									2	28		3	2	47			3 2	0,5 15 2	2
																				2														2				2						2
																											cos m, n 15n
252 141 60 453
252 141 60 453


	b	b			2					4m 5n				2	16m				2		40	m		n									2			16	3		2	40		3 2 0,5 25 2			2
					2									2					2														2						2						2
																										cos m, n 25n


			144 120 100											364
Окончательно получаем:
пр				a b					453
			b
									364


в)
в)			сos a, b

a 3m 2n											b 4m 5n

Так как

d a 3m 2n e b 4m 5n

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

					d e
Тогда сos d, e
Тогда сos d, e
					d	e
Находим d e
d e 3m 2n				4m 5n 12m									2		7		m	n						10n			2		12 3			2	7 3 2	0,5 10 2				2	108 21	40 89
													2														2					2						2
																			cos m, n



			2					2														2						2							2
	d		2				9m	2	12		m		n								4n	2				9 3		2	12 3 2 0,5 4					2	2		81 36 16				61 7,81
	d	3m 2n					9m		12		m		n		cos m, n						4n					9 3			12 3 2 0,5 4					2			81 36 16				61 7,81



	e	4m 5n	2			16m			2	40		m		n									2		16				3	2	40 3 2 0,5			25 2		2
			2						2														2							2						2
																cos m, n				25n

144 120 100 364 19,08

Врезультате имеем:

	89		89	0,597
сos a, b
	7,81	19,08	149

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

2. По координатам точек А, В и С для указанных векторов найти: а) модуль вектора а; б) скалярное произведение векторов а и b; в) проекцию вектора c на вектор d; г) координаты точки М, делящей отрезок l в отношении α : β

2.0 A(5, 4, 4), B(2, 4, 6), C(5, –2, 6) a = –2 BC + 4 BA , b =c= CA , d = BA , l=BC, α = 3, β = 1

а) модуль вектора а

Последовательно находим

BA 5 2; 4 4; 4 6 3; 0; 2 ; 4BA 12; 0; 8

BC 5 2; 2 4; 6 6 3; 6; 0

2BC 6; 12; 0

2BC 4BA 6 12; 12 0; 0 ( 8) 6; 12; 8

Модуль вектора определяем выражением

a 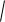x12 y12 z12

Тогда Модуль вектора а:

		62 122 ( 8)2
a	2BC 4BA	62 122 ( 8)2	36 144 64 244

б) скалярное произведение векторов а и b

a2BC 4BA 6; 12; 8

bCA 0; 6; 2

Скалярное произведение двух векторов находим по формуле

a b x1x2 y1y2 z1z2

Тогда

a b 6 0 12 6 ( 8) ( 2) 0 72 16 88

в) проекцию вектора c на вектор d;

Так как пр d c	c d		c		0; 6; 2
	c d			CA
		d

d BA 3; 0; 2

c d 0 3 6 0 ( 2) ( 2) 0 4 4 d 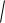32 02 ( 2)2 9 4 13

			4
пр		CA	4

	BA
	BA		13
			13

г) координаты точки М, делящей отрезок l в отношении 3 :1

B(2, 4, 6), C(5, –2, 6)

Имеем: 3			r		rB rC		. Следовательно,
Имеем: 3			r				. Следовательно,
			M			1
						1
x M		2 3 5	17				yM		4 3 ( 2)				2	1
x M		1 3	4				yM						4	2
		1 3	4							1 3			4	2
zM	6 3 6		24	6				17			1
							M			;		; 6
		1 3	4				M	4		;	2	; 6
		1 3	4					4			2

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

3.Доказать, что векторы a,b,c образуют базис, и найти координаты вектора d в этом базисе.

3.0a(2, –1, 2); b(1, 1, 2); c(4, 1, 4); d(8, 11, 22)

Вычисляем по правилу треугольника:

a	11	a12	a13
				a11a 22a 33	a12a 23a 31 a 21a 32a13 a13a 22a 31 a12a 21a 33 a 23a 32a11
a	21	a 22	a 23	a11a 22a 33	a12a 23a 31 a 21a 32a13 a13a 22a 31 a12a 21a 33 a 23a 32a11
		a 32	a 33
a 31		a 32	a 33

Тогда
		1	2
	2	1	2
abc	1	1	2	2 1 4 ( 1) 2 4 2 1 1 2 1 4 2 2 1 ( 1) 1 4 8 8 2 8 4 4 6 0
	4	1	4

Следовательно, векторы a,b,c образуют базис, и вектор d линейно выражается через базисные векторы: d a b c

или в координатной форме

2 4 811 2 2 4 22

Решаем полученную систему по формулам Крамера. Находим:

2	1	4
1 1		1	8 2 8 8 4 4 6
2	2	4

Найдем
						1	4
				8		1	4
				11		1	1	32 22 88 88 16 44 6
				22		2	4
						8	4
			2			8	4
			1			11	1		88 16 88 88 44 32 84
			2			22	4
						1	8
		2				1	8
		1				1	11	44 22 16 16 44 22 12
		2				2	22
					;		;

	6				1;					84	14;	12	2
	6				1;					6	14;		2
	6									6		6
Поэтому d 1;							14; 2 a 14b 2c

Соседние файлы в предмете Математика

#
20.02.2017252.34 Кб69ИДЗ 13.3 Рябушко пример решения.pdf
#
20.02.2017248.61 Кб99ИДЗ 14.1 Рябушко пример решения.pdf
#
20.02.2017189.82 Кб47ИДЗ 14.2 Рябушко пример решения.pdf
#
20.02.2017305.45 Кб101ИДЗ 15.1 Рябушко пример решения.pdf
#
20.02.2017240.54 Кб87ИДЗ 15.2 Рябушко пример решения.pdf
#
20.02.2017255.44 Кб499ИДЗ 2.1 Рябушко пример решения.pdf
#
20.02.2017248.21 Кб305ИДЗ 2.2 Рябушко пример решения.pdf
#
20.02.2017218.55 Кб342ИДЗ 3.1 Рябушко пример решения.pdf
#
20.02.2017229.13 Кб226ИДЗ 3.2 Рябушко пример решения.pdf
#
20.02.2017311.11 Кб263ИДЗ 4.1 Рябушко пример решения.pdf
#
20.02.2017220.66 Кб304ИДЗ 5.1 Рябушко пример решения.pdf