5. Расчет доверительных интервалов

Доверительный интервал - термин, используемый в математической статистике при интервальной оценке статистических параметров, что предпочтительнее при небольшом объёме выборки.

Доверительный интервал для математического ожидания

Найдем доверительный интервал для математического ожидания при условии, что дисперсия генеральной величины неизвестна, а доверительная вероятность равна 1 – α.

Для расчета доверительного интервала применим формулу:

x – среднее значение величины

–квантиль распределения Стьюдента с степенью свободы

–несмещенное выборочное стандартное отклонение

–объем выборки

1. Определим квантиль распределения Стьюдента, для этого воспользуемся стандартной таблицей:

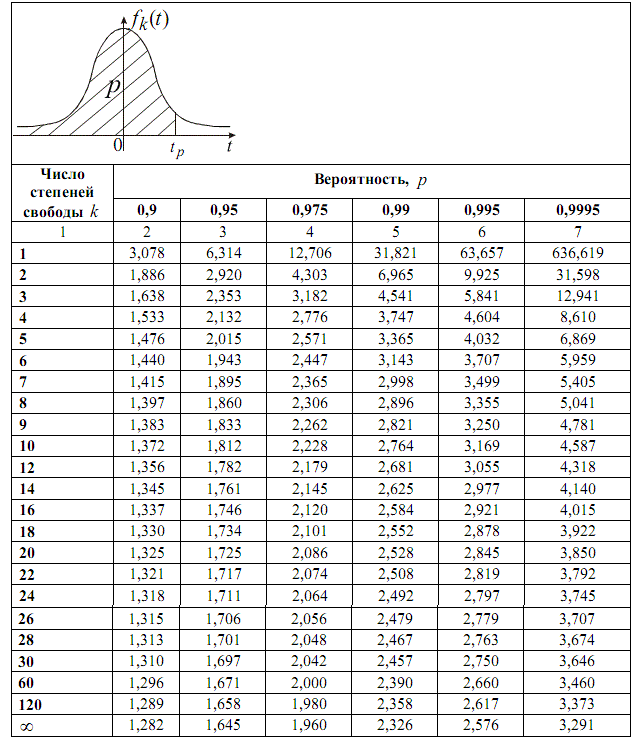
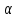возьмем равным 0,05.

Выберем значение = 2,571

1. Найдем S:

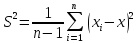
10.15

2.94

2. Подставим все известные значения в формулу из пункта 1):

Для M[X]:

Для M[Y]:

Доверительный интервал для дисперсии

Найдем доверительный интервал для дисперсии при условии, что среднее значение величины неизвестно, а доверительная вероятность равна 1 – α.

Для расчета доверительного интервала применим формулу:

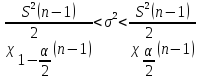
–дисперсия

–несмещенное выборочная дисперсия

–квантиль распределения со степенями свободы.

1. Определим квантиль распределения , для этого воспользуемся специальной таблицей:

12,8325

0,8312

2. Подставим найденные значения в формулу из пункта 1):

Для Х:

Для У:

Доверительный интервал для корреляции

Найдем доверительный интервал для корреляции при условии, что выборка получена из генеральной совокупности, r – выборочный коэффициент корреляции.

Для расчета доверительного интервала применим формулу:

1. Рассчитаем :

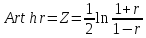
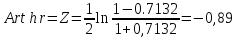
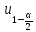2. возьмем из таблицы квантилей нормального распределения:

3. Подставим все в формулы:

4. Найдем с помощью таблицы гиперболических тангенсов:

6. Проверка гипотез

Таким образом было установлено, что между заработной платой сотрудников ДПС и количеством оштрафованных существует связь. Искомая корреляция равна -0.7132. Это высокая степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0,7 до 0,99. Нам удалось выявить зависимость, и результаты в данном случае оказались вполне ожидаемы. Чем выше средняя заработная плата по субъекту РФ, тем меньше оштрафованных. Почему получились такие результаты, нам остается только гадать. Да и не было нашей целью объяснять почему именно так. Мы должны были, ради личного интереса, посмотреть есть ли связь.

7. Регрессия

Любая нелинейная регрессия, в которой уравнение регрессии для изменений в одной переменной (у) как функции t изменений в другой (х) является квадратичным, кубическим или уравнение более высокого порядка. Хотя математически всегда возможно получить уравнение регрессии, которое будет соответствовать каждой "загогулине" кривой, большинство этих пертурбаций возникает в результате ошибок в составлении выборки или измерении, и такое "совершенное" соответствие ничего не дает. Не всегда легко определить, соответствует ли криволинейная регрессия набору данных, хотя существуют статистические тесты для определения того, значительно ли увеличивает каждая более высокая степень уравнения степ совпадения этого набора данных.

Теперь, будем считать, что выборочная криволинейная регрессия определяется уравнением:

Коэффициенты называются выборочными коэффициентами регрессии.

Из ранее изученных пунктов, нам известны следующие параметры:

х = 20,35

у = 9,47

= 85,79

= 7,21

= -0.71

Теперь мы можем подставить все значения в уравнение: