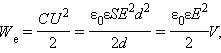7. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов при переносе каждой порции Δq внешние силы должны совершить работу

Энергия W_е конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

 

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.

Электрическую энергию W_е следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для W_е аналогичны формулам для потенциальной энергии E_р деформированной пружины (см. ч. I, § 2.4)

где k – жесткость пружины, x – деформация, F = kx – внешняя сила.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора. Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость Поэтому

где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина

является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.

Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности w_е по всему объему, в котором создано электрическое поле.

Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладает потенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.

Рассмотрим сначала систему, состоящую из двух точечных зарядов. Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая q₂ к q₁ либо q₁ к q₂. В обоих случаях совершается одинаковая работа:

В последней формуле - потенциал поля 1-го заряда в том месте, где находится второй заряд; - потенциал поля второго заряда в том месте, где находится первый заряд. С учетом сказанного, эту формулу можно записать также в виде:

.

Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов может быть представлена в виде:

 

 

 

В общем случае системы n неподвижных точечных зарядов энергия системы определяется по формуле: .

Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладает потенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.

Рассмотрим сначала систему, состоящую из двух точечных зарядов. Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая q₂ к q₁ либо q₁ к q₂. В обоих случаях совершается одинаковая работа:

В последней формуле - потенциал поля 1-го заряда в том месте, где находится второй заряд; - потенциал поля второго заряда в том месте, где находится первый заряд. С учетом сказанного, эту формулу можно записать также в виде:

.

Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов может быть представлена в виде:

 

 

 

В общем случае системы n неподвижных точечных зарядов энергия системы определяется по формуле: .

Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладает потенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.

Рассмотрим сначала систему, состоящую из двух точечных зарядов. Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая q₂ к q₁ либо q₁ к q₂. В обоих случаях совершается одинаковая работа:

В последней формуле - потенциал поля 1-го заряда в том месте, где находится второй заряд; - потенциал поля второго заряда в том месте, где находится первый заряд. С учетом сказанного, эту формулу можно записать также в виде:

.

Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов может быть представлена в виде:

 

 

 

В общем случае системы n неподвижных точечных зарядов энергия системы определяется по формуле: .

Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладает потенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.

Рассмотрим сначала систему, состоящую из двух точечных зарядов. Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая q₂ к q₁ либо q₁ к q₂. В обоих случаях совершается одинаковая работа:

В последней формуле - потенциал поля 1-го заряда в том месте, где находится второй заряд; - потенциал поля второго заряда в том месте, где находится первый заряд. С учетом сказанного, эту формулу можно записать также в виде:

.

Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов может быть представлена в виде:

 

 

 

В общем случае системы n неподвижных точечных зарядов энергия системы определяется по формуле: .

Если проводник поместить во внешнее электростатическое поле или зарядить его, то на заряды данного проводника будет действовать электростатическое поле, под действием которого они начнут двигаться. Движение зарядов (ток) будет длиться до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри данного проводника обращается в нуль. Это происходит в течение очень короткого времени. Действительно, если бы поле не было равно нулю, то в проводнике появилось бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что не согласуется с законом сохранения энергии. Значит, напряженность поля во всех точках внутри проводника равна нулю:    Если внутри проводника электрического поле отсутствует, то потенциал во всех точках внутри проводника одинаков (φ = const), т. е.поверхность проводника в электростатическом поле является эквипотенциальной. Это означает, что вектор напряженности поля на внешней поверхности проводника направлен по перпендикуляру к каждой точке его поверхности. Если это было бы не так, то под действием касательной составляющей Е заряды начали бы перемещаться по поверхности проводника, что, в свою очередь, противоречило бы равновесному распределению зарядов.  Если проводнику дать некоторый дополнительный заряд Q, то нескомпенсированные заряды разместяться только на поверхности проводника. Это вытекает непосредственно из теоремы Гаусса, согласно которой заряд Q, который находится внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равен    поскольку во всех точках внутри замкнутой поверхности D=0.  Теперь мы будем искать взаимосвязь между напряженностью Е поля вблизи поверхности заряженного проводника и поверхностной плотностью зарядов на его поверхности σ . Для этого используем теорему Гаусса для бесконечно малого цилиндра с основаниями ΔS, который пересекает границу проводник—диэлектрик. Ось цилиндра направлена вдоль вектора Е (рис. 1). Поток вектора электрического смещения через внутреннюю часть цилиндрической поверхности равен нулю, так как внутри проводника Е₁ (а следовательно, и D₁) есть нуль, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Используя теорему Гаусса, этот поток (DΔS) равен сумме зарядов (Q=σΔS), находящихся внутри поверхности: DΔS=σΔS т.е.   (1)  или   (2)  где ε — диэлектрическая проницаемость среды, находящаяся вокруг проводника.  Значит, напряженность электростатического поля у поверхности проводника задается поверхностной плотностью зарядов. Можно показать, что формула (2) задает напряженность электростатического поля вблизи поверхности проводника абсолютно произвольной формы.  Если во внешнее электростатическое поле поместить нейтральный проводник, то свободные заряды (электроны, ионы) будут совершать движение: положительные — по полю, отрицательные — против поля (рис. 2, а). На одном конце проводника будет собираться избыток положительного заряда, на другом — избыток отрицательного заряда. Эти заряды называются индуцированными (наведенными). Процесс будет продолжаться до тех пор, пока внутри проводника напряженность поля не станет равной нулю, а линии напряженности вне проводника — перпендикулярными его поверхности (рис. 2, б). Значит, нейтральный проводник, который внесен в электростатическое поле, разрывает часть линий напряженности; эти линии напряженности заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности нашего проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией.  Из рис. 2, б мы видим, что индуцированные заряды образуются на проводнике вследствие смещения их под действием поля, т. е. σ есть поверхностной плотностью смещенных зарядов. Согласно (1), электрическое смещение D вблизи проводника численно равно поверхностной плотности смещенных зарядов. По этой причине вектор D получил название вектора электрического смещения. 

Поскольку в состоянии равновесия заряды отсутствуют внутри проводника, то создание внутри него полости не окажет влияния на конфигурацию расположения зарядов и тем самым на электростатическое поле. Значит, поле будет отсутствовать внутри полости. Если теперь заземлить данный проводник с полостью, то потенциал во всех точках полости будет равен нулю, т. е. полость полностью является изолированной от влияния внешних электростатических полей. На этом основана электростатическая защита — экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Для защиты вместо сплошного проводника может быть использована густая металлическая сетка, которая, также эффективна при наличии не только постоянных, но и переменных электрических полей.  Свойство зарядов располагаться на внешней поверхности проводника на практике используется для устройства электростатических генераторов, которые предназначены для накопления больших зарядов и достижения разности потенциалов в несколько миллионов вольт. Электростатический генератор, который изобретен американским физиком Р. Ван-де-Граафом (1901—1967), состоит из шарообразного полого проводника 1 (рис. 3), укрепленного на изоляторах 2. Движущаяся замкнутая лента 3 из прорезиненной ткани заряжается от источника напряжения с помощью системы остриев 4, которые соединены с одним из полюсов источника, второй полюс которого заземлен. Заземленная пластина 5 усиливает стекание зарядов с остриев на ленту. Другая система остриев 6 снимает заряды с ленты и передает их полому шару, и они переходят на его внешнюю поверхность. Значит, сфера постепенно получает большой заряд и удается достичь разности потенциалов в несколько миллионов вольт. Электростатические генераторы широко применяются в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике. 

Индуцированные заряды - это заряды противоположного знака, появившиеся в результате разделения у концов проводника.

Результирующие поле определяется как суперпозиция внешнего поля и поля

индуцированных зарядов. Перераспределение зарядов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды внутри тела практически полностью не скомпенсируют внешнее электрическое поле. При этом на противоположных сторонах проводящего тела появятся противоположные индуцированные заряды.

Экранировка электростатического поля: Если внесенное во внешнее электрическое поле тело не было заряжено, то сумма наведенных на нем зарядов оказывается равной нулю. Эти заряды распределяются так, чтобы их поле внутри проводящего тела в точности скомпенсировало внешнее поле. Ничто не изменится, если проводящее тело будет полым – во всей полости тела поле также будет отсутствовать. Этим обстоятельством широко пользуются для электростатического экранирования различных приборов и аппаратов от внешних электрических полей. С этой целью приборы помещают в замкнутые металлические оболочки, называемые экранами. Как показывает опыт, экраны можно выполнять и из мелкой металлической сетки.

Если экран заземлить, то такой экран способен в равной мере защищать внешнее пространство от поля зарядов, помещенных внутри экрана.