
- •Электричество
- •Электрическое поле – силовое поле, посредством которого взаимодействуют электрические заряды.
- •Теорема Гаусса для электростатического поля:
- •Если цилиндр радиуса r имеет поверхностную плотность заряда s, а внутри его зарядов нет, то получаем:
- •Теперь изучим поведение диполя во внешнем электрическом поле. Пусть диполь помещен в однородное электрическое поле (см. Рис. 1.16).
- •Диэлектриками называют тела, не проводящие электрического тока.
- •Имеем границу раздела двух сред с и , так что, (рис. 4.10, а).
- •, Отсюда можно записать:
- •Расчет напряженности и разности потенциалов некоторых электростатических полей
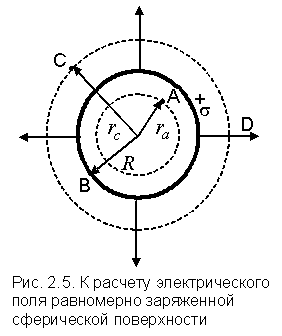
- •Пример 2. Электрическое поле равномерно заряженной сферической поверхности.
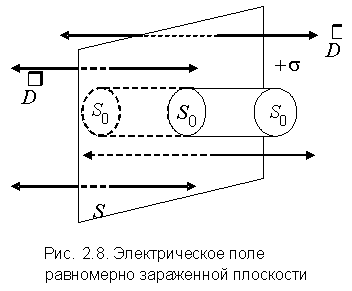
- •Пример 3. Электрическое поле равномерно заряженной плоскости
- •Пример 5. Электрическое поле диполя.
- •Электроемкость уединенного проводника.
- •Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Пример 2. Электрическое поле равномерно заряженной сферической поверхности.
Рассмотрим
электрическое поле, создаваемое
заряженной сферической поверхностью
(рис. 2.5). Пусть заряд равномерно распределен
по поверхности сферы с поверхностной
плотностью
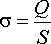 .
Из условия задачи очевидно, что линии
электрического смещения могут быть
только перпендикулярны заряженной
поверхности и расходиться радиально
от центра. Поэтому в качестве замкнутой
поверхности удобно выбрать сферу с
радиусом
.
Из условия задачи очевидно, что линии
электрического смещения могут быть
только перпендикулярны заряженной
поверхности и расходиться радиально
от центра. Поэтому в качестве замкнутой
поверхности удобно выбрать сферу с
радиусом
![]() .
.
Исследуем электрическое поле в точках А, В и С (рис. 2.5):
|
|
а)
рассмотрим точки электрического поля
внутри шара. Выберем произвольную
точку А и проведем через нее сферическую
поверхность с радиусом
Равенство (2.13) выполняется при условии, что
Следовательно, в любой точке, расположенной внутри заряженной сферической поверхности, вектор электрического смещения равен нулю. |
Используя
условия:
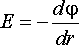 и
и
![]() ,
из формулы (2.14) следует
,
из формулы (2.14) следует
![]() .
(2.15)
.
(2.15)
Формула (2.15) указывает, что все точки внутри сферы имеют одинаковые потенциалы;
б)
рассмотрим точки поля на поверхности
сферы. Выберем сферическую поверхность
с радиусом
![]() и
запишем теорему Остроградского–Гаусса
и
запишем теорему Остроградского–Гаусса
![]() ,
,
где
![]() –
заряд, распределенный по поверхности
сферы.
–
заряд, распределенный по поверхности
сферы.
Из
условия симметрии задачи очевидно, что
![]() для
всех точек сферической поверхности.
Интегрирование по замкнутой поверхности
радиусом
для
всех точек сферической поверхности.
Интегрирование по замкнутой поверхности
радиусом
![]() дает
дает
![]() .
.
Так
как
![]() ,
то имеем
,
то имеем
![]() или
или
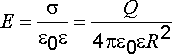 ;
(2.16)
;
(2.16)
в)
рассмотрим точки поля за пределами
сферической поверхности. Выберем
произвольную точку С и проведем
через нее сферическую поверхность с
радиусом
![]() .
Для выбранной поверхности запишем
теорему Остроградского–Гаусса
.
Для выбранной поверхности запишем
теорему Остроградского–Гаусса
![]() ,
,
где
![]() ;
;
![]() –
заряд на поверхности сферы.
–
заряд на поверхности сферы.
Из
условия симметрии задачи опять очевидно,
что
![]() для
всех точек выбранной поверхности. После
интегрирования по замкнутой поверхности
радиусом
для
всех точек выбранной поверхности. После
интегрирования по замкнутой поверхности
радиусом
![]() получаем
получаем
![]() .
.
После упрощения имеем
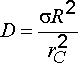 или
или
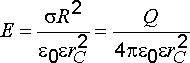 .
(2.17)
.
(2.17)
Используя
формулу (2.17) и условия
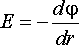 и
и
![]() ,
получаем
,
получаем
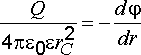 ,
откуда
,
откуда
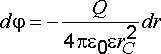 .
.
Проинтегрируем полученное выражение
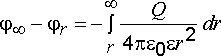 ,
,
принимая
![]() ,
получаем
,
получаем
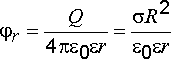 .
(2.18)
.
(2.18)
Потенциал
поверхности сферы определим из (2.18),
используя условие
![]() ,
,
 .
(2.19)
.
(2.19)
Графики
зависимости
![]() и
j от расстояния до центра заряженной
сферической поверхности представлены
на рис. 2.6 и 2.7.
и
j от расстояния до центра заряженной
сферической поверхности представлены
на рис. 2.6 и 2.7.

Рис.
2.6. Зависимость
![]() электрического
Рис. 2.7. Зависимость
электрического
Рис. 2.7. Зависимость
![]() электрического
поля
электрического
поля
поля заряженной сферы заряженной сферы
Пример 3. Электрическое поле равномерно заряженной плоскости
Имеется
безграничная плоскость, заряженная
равномерно с поверхностной плотностью
![]() .
Из симметрии задачи очевидно, что линии
смещения могут быть направлены только
перпендикулярно плоскости и равномерно
распределены по поверхности. При записи
теоремы Остроградского–Гаусса в
качестве замкнутой поверхности удобно
выбрать прямой цилиндр, перпендикулярный
заряженной плоскости, ограниченный
двумя плоскими основаниями площадью
.
Из симметрии задачи очевидно, что линии
смещения могут быть направлены только
перпендикулярно плоскости и равномерно
распределены по поверхности. При записи
теоремы Остроградского–Гаусса в
качестве замкнутой поверхности удобно
выбрать прямой цилиндр, перпендикулярный
заряженной плоскости, ограниченный
двумя плоскими основаниями площадью
![]() ,
расположенными по обеим сторонам
заряженной плоскости (рис. 2.8).
,
расположенными по обеим сторонам
заряженной плоскости (рис. 2.8).
Полный поток электрического смещения через выбранную замкнутую поверхность
![]() .
.
|
|
Так
как образующие цилиндра параллельны
линиям смещения ( Применяя теорему Остроградского–Гаусса, имеем
откуда
|
Напряженность поля равномерно заряженной плоскости
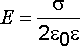 .
(2.21)
.
(2.21)
Из (2.21) вытекает, что безграничная заряженная плоскость создает однородное электрическое поле.
Потенциалы поля изменяются только в направлении, перпендикулярном плоскости, и разность потенциалов между точками в этом направлении определится как
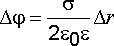 .
(2.22)
.
(2.22)
Пример
4. Поле равномерно заряженного цилиндра
(нити).
Рассмотрим безграничный цилиндр (нить),
равномерно заряженный по длине с линейной
плотностью заряда
![]() ,
где d –
длина цилиндра.
,
где d –
длина цилиндра.
Из условия симметрии линии смещения будут радиальными прямыми, перпендикулярными к поверхности цилиндра. В этом случае в качестве поверхности для вычисления потока удобно выбрать цилиндрическую поверхность S показанную на рис. 2.9.
Так
как поток через основание выбранного
цилиндра равен нулю (![]() ),
а боковая поверхность перпендикулярна
к линиям смещения (
),
а боковая поверхность перпендикулярна
к линиям смещения (![]() ),
то полный поток через замкнутую
поверхность
),
то полный поток через замкнутую
поверхность
![]() .
.
|
|
Применяя теорему Остроградского–Гаусса, имеем
Отсюда
получаем, что электрическое смещение
поля в точках, отстоящих на расстоянии
С учетом выражения (2.2) напряженность электрического поля, созданного заряженным цилиндром (нитью), составит
|
Так
как
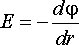 ,
то с учетом (2.24) разность потенциалов
между точками, удаленными от оси цилиндра
на расстояние
,
то с учетом (2.24) разность потенциалов
между точками, удаленными от оси цилиндра
на расстояние
![]() ,
определится по формуле
,
определится по формуле
 (2.25)
(2.25)
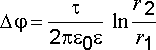 .
.
Выражения (2.24) и (2.25) показывают, что электрическое поле, создаваемое заряженным цилиндром (нитью), имеет цилиндрическую симметрию.

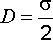 .
(2.20)
.
(2.20)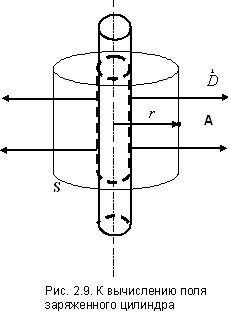
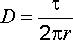 .
(2.23)
.
(2.23)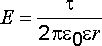 .
(2.24)
.
(2.24)