Если цилиндр радиуса r имеет поверхностную плотность заряда s, а внутри его зарядов нет, то получаем:

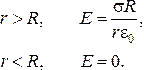(23.18)

в) Поле равномерно заряженного шара радиуса R

Пусть имеем шар радиуса R, заряженный равномерно по всему объему с плотностью заряда r. Из соображений симметрии электрическое поле направлено радиально

 

 

. Сначала находим поле вне шара. Для этого окружаем шар сферой радиуса r > R и находим поток вектора напряженности электрического поля, который по теореме Гаусса равен полному заряду внутри сферы:

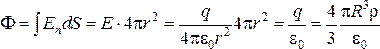. (23.19)

Отсюда получим поле, совпадающее с полем точечного заряда:

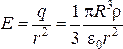. (23.20)

Для определения поля внутри шара выбираем соответствующую поверхность: сферу внутри шара r < R. Тогда по теореме Гаусса

.

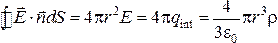Отсюда получим поле внутри равномерно заряженного шара:

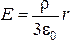. (23.21)

Соотношение (3-8) легко записать в векторном виде, поскольку поле внутри шара направлено по радиусу:

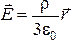. (23.22)

1. Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.

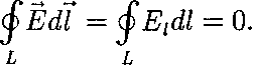
Этот интеграл называется циркуляцией вектора напряженности. Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным.

Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.

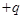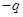2. Определение. Электрическим диполем называется система двух одинаковых по величине и противоположных по знаку зарядов и , расстояние 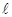между которыми много меньше расстояния до тех точек, в которых определяется электрическое поле системы. Осью диполя называется прямая, проходящая через оба заряда.

Потенциал поля системы зарядов и находится в любой точке в соответствии с (1.24) и рис. 1.13 как

 

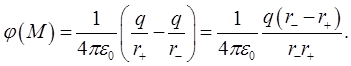(1.35)

 

Так как , то приближенно можно положить

 

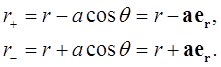(1.36)

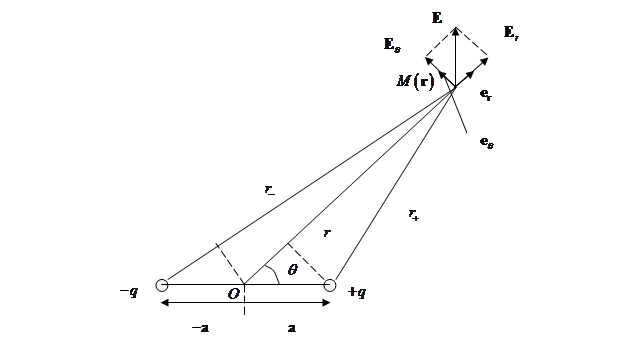
Рис. 1.13. К расчету электрического поля диполя, ,

точка - начало системы координат

 

Отсюда Кроме того, при имеем: . Вместо (1.35) приближенно получаем

 

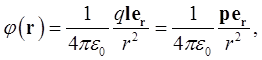(1.37)

 

где - электрический момент диполя,

 

(1.38)

 

Вектор направлен вдоль оси диполя от отрицательного заряда к положительному (см. рис. 1.14).

 

Рис. 1.14. Электрический момент диполя

 

Из (1.38) видно, что поле диполя определяется его электрическим моментом. Потенциал поля диполя убывает с расстоянием от него по закону , то есть быстрее, чем потенциал точечного заряда (). Поле диполя обладает осевой симметрией относительно оси диполя. Так как , то в полярной системе координат выражение (1.37) запишется как

 

(1.39)

 

В полярной системе координат оператор «набла» записывается как

 

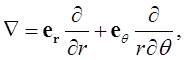(1.40)

 

где и - базисные векторы данной системы координат (см. рис. 1.13).

Подставим (1.40) в (1.33), получим выражение напряженности электрического поля диполя через потенциал в полярных координатах:

 

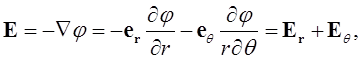(1.41)

 

где с учетом (1.39)

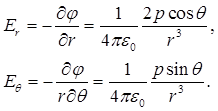(1.42)

 

Модуль напряженности поля диполя

 

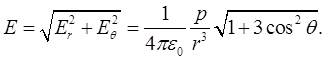(1.43)

 

Напряженность поля диполя убывает с расстоянием от него по закону , то есть быстрее, чем напряженность поля точечного заряда ().

Картина силовых линий электрического поля системы зарядов и показана на рис. 1.15.

 

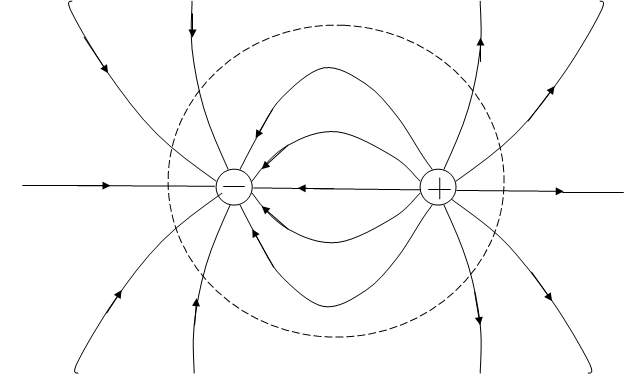
Рис. 1.15. Картина силовых линий электрического поля системы зарядов и , формулы (1.40), (1.42) и (1.43) для поля диполя приближенно справедливы

вне сферы (пунктирная линия) достаточно большого радиуса ,

где - расстояние между зарядами

 

Плоскость (перпендикулярна оси диполя и проходит через его середину) является эквипотенциальной: .