3. Теперь изучим поведение диполя во внешнем электрическом поле. Пусть диполь помещен в однородное электрическое поле (см. Рис. 1.16).

На диполь действует момент электрической силы

 

(1.44)

 

где , , , откуда или

 

(1.45)

 

где электрический момент диполя .

Рис. 1.16. Диполь в однородном поле

 

Момент сил (1.45) стремится повернуть диполь так, чтобы его электрический момент установился в направлении электрического поля .

Найдем потенциальную энергию, которой обладает диполь во внешнем электрическом поле (см. рис. 1.17):

 

(1.46)

 

Рис. 1.17. К расчету потенциальной энергии диполя во внешнем поле

 

Потенциал однородного поля убывает линейно в направлении вектора . Поэтому

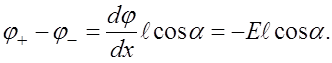(1.47)

 

Подставим (1.47) в (1.46), найдем

 

(1.48)

 

или в векторных обозначениях

(1.49)

 

Формулы (1.45) и (1.49) остаются справедливыми и в неоднородном электрическом поле, так как размером диполя пренебрегается по сравнению с характерным размером неоднородности поля.

В неоднородном внешнем электрическом поле на диполь действует сила

 

(1.50)

 

Формула (1.50) показывает, что в неоднородном поле на диполь действует сила, направленная в сторону наиболее быстрого уменьшения потенциальной энергии диполя в этом поле. Сила приводит диполь в поступательное движение. Проиллюстрируем данный вывод на конкретных примерах (см. рис. 1.18).

 

Рис. 1.18. Поведение диполя в неоднородном поле

 

В случае рис. 1.18, а диполь втягивается в область более сильного поля, так как , и сила , действующая на диполь, направлена слева направо. Аналогично можно показать, что диполь, ориентированный против поля, выталкивается из поля. В случае рис. 1.18, б сила , действующая на диполь, направлена вверх (в направлении ослабления поля) – диполь смещается вверх, параллельно самому себе.

4. Диэлектриками называют тела, не проводящие электрического тока.

Термин «диэлектрик» введен М. Фарадеем для обозначения ве­ществ, через которые проникают электрические поля, в отличие от металлов, внутри которых электростатического поля нет. К ди­электрикам относят твердые тела, такие, как эбонит, фарфор, а также жидкости (например, чистая вода) и газы.

При изменении внешних условий (нагревание, воздействие ионизирующих излучений и т. п.) диэлектрик может проводить электрический ток. Изменение состояния диэлектрика при помещении в электрическое поле можно объяснить его молекулярным строением. Условно выделим три класса диэлектриков: 1) полярные; 2) неполярные; 3) кристаллические.

К первому классу принадлежат такие вещества, как вода, нитробензол и др. Молекулы этих диэлектриков не симметричны, «центры масс» их положительных и отрицательных зарядов не совпада­ют, поэтому такие молекулы обладают электрическим дипольным моментом даже в случае, когда электрического поля нет.

На рис. 12.19 схематически показаны молекулы соляной кислоты (а) и воды (б) и соответствующие им дипольные моменты в дебаях¹. (¹ Дебай (Д) — внесистемная единица дипольного момента молекул: 1Д = 3,33564 • 10^-30Кл • м.)

 

 

В отсутствие электрического поля дипольные моменты молекул ориентированы хаотически (рис. 12.20, а) и векторная сумма моментов всех N молекул равна нулю:

Если диэлектрик поместить в электрическое поле, то дипольные моменты молекул стремятся ориентироваться вдоль поля (рис. 12.20, б), однако полной ориентации не будет вследствие молекулярно-теплового хаотического движения. В этом случае

 

Ко второму классу диэлектриков относят такие вещества (например, водород, кислород и др.), молекулы которых в отсутствие электрического поля не имеют дипольных моментов. В таких мо­лекулах заряды электронов и ядер расположены так, что «центры масс» положительных и отрицательных зарядов совпадают. Если неполярную молекулу поместить в электрическое поле, то разно­именные заряды несколько сместятся в противоположные стороны и молекула будет иметь дипольный момент. На рис. 12.21 схе­матически в виде кружков показаны молекулы такого диэлектри­ка в отсутствие поля (а) и при наложении поля (б)(стрелки у кружков означают дипольные моменты молекул).

Третий класс — кристаллические диэлектрики (например, NaCl), решетка которых состоит из положительных и отрицательных ионов. Такой диэлектрик можно схематически рассматривать как совокупность двух «подрешеток», одна из которых заря­жена положительно, другая — отрицательно. При отсутствии поля подрешетки расположены симметрично и суммарный электрический момент такого диэлектрика равен нулю¹. (¹ Строго говоря, ионные кристаллы могут обладать электрическим моментом и при отсутствии внешнего поля, однако здесь это не учтено.) Если диэлектрик поместить в электрическое поле, то подрешетки немного сместятся в противоположные стороны и диэлектрик приобретет электрический момент.

Все эти процессы, происходящие в разных диэлектриках при наложении электрического поля, объединяют общим термином поляризация, т. е. приобретение диэлектриком дипольного мо­мента.

Для первого класса диэлектриков характерна ориентационная поляризация, для второго — электронная, т. е. смещение глав­ным образом электронных оболочек, для третьего — ионная. Та­кая классификация условна, так как в реальном диэлектрике могут одновременно существовать все виды поляризации.

Изменение напряженности электрического поля, в котором на­ходится диэлектрик, будет влиять на состояние его поляризации. Охарактеризовать степень поляризации диэлектрика суммарным электрическим моментом всех его N молекул нельзя, так как эта величина зависит, в частности, от объема диэлектрика. Для оценки состояния поляризации диэлектрика вводят величи­ну, называемую поляризованностъю, среднее значение которой равно отношению суммарного электрического момента элемента объема V диэлектрика к этому объему:

(12.36)

Единицей поляризованности является кулон на квадратный метр (Кл/м²).

При поляризации диэлектрика на одной его поверхности (гра­ни) создаются положительные заряды, а на другой — отрицатель­ные (см. рис. 12.20, б и 12.21, б). Эти электрические заряды называют связанными, так как они принадлежат молекулам диэлект­рика (или кристаллической решетке при ионной поляризации) и не могут перемещаться в отрыве от молекул или быть удалены с поверхности диэлектрика в отличие от свободных зарядов, кото­рых в идеальном диэлектрике нет.

При возрастании напряженности электрического поля растет степень упорядоченности ориентации молекул (ориентационная поляризация), увеличиваются дипольные моменты молекул (электронная поляризация), а также происходит большее смещение «подрешеток» (ионная поляризация) — все это приводит к увеличению поверхностной плотности s_св связанных электриче­ских зарядов.

Таким образом, s_св также характеризует степень поляризации диэлектрика.

Установим связь между Р_е и s_св на примере поляризованного диэлектрика, имеющего форму параллелепипеда (рис. 12.22, а). Такой параллелепипед представим как совокупность диполей, которые, простоты ради, можно рассматривать как «цепочки»; одна из них показана на рис. 12.22, б. Так как внутренние части «цепочки» диполей электрически компенсируются, то такая «цепочка» подобна длинному диполю с расстоянием между зарядами, равным ребру параллелепипеда.

Если на грани параллелепипеда с площадью S возник связанный заряд </_ов, то суммарный электрический моментвсего параллелепипе­да численно равен д_св /, но так как Объем парал­лелепипеда V = SI cos a. На основании двух последних равенств имеем

(12.37)

Учитывая (12.36) и (12.37), получаем

откуда

Итак, поверхностная плотность связанных зарядов s_св равна нор­мальной к грани составляющей вектора Р_е.

Рассмотрим, например, плоский диэлектрик, расположенный в однородном электрическом поле (рис. 12.23); — напряженность поля в отсутствие диэлектрика (поле в вакууме). Связанные заряды создают однородное поле напряженностью , в результа­те в диэлектрике будет электрическое поле напряженностью

Е = Е₀- Е_св(12.39)

 

Известно, что диэлектрическая проницаемость среды e равна отношению силы взаимодействия зарядов в вакууме к силе взаимодействия этих же зарядов на том же расстоянии в среде:

F₀/F = e, или F₀ = eF.

Так как напряженность электрического поля пропорциональна силе, действующей на заряд [см. (12.1)], то аналогичное соотноше­ние можно записать для Е₀ и Е:

Е₀ = eЕ. (12.40)

Напряженность электрического поля, об­разованного связанными электрическими зарядами, Е_св = s_св/e₀. Для данного примера из (12.38) имеем s_св = Р_е, тогда Е_св = Р_е/e₀. Подставляя эту форму­лу и (12.40) в (12.39), получаем Е = eЕ - Р_е/e₀, или Е(e₀ - 1) = = Р_е/e₀, откуда

Р_е = e₀(e- 1)Е. (12.41)

Как и можно было ожидать, поляризованность пропорциональна напряженности электрического поля в диэлектрике. На основании (12.41) вводят понятие диэлектрической восприимчивости среды

c = e-1, (12-42)

которая вместе с диэлектрической проницаемостью e характеризует способность диэлектрика к поляризации и зависит от его мо­лекулярного строения, а возможно и от температуры. В переменных электрических полях eиc изменяются также в зависимости от частоты.