
- •Электричество
- •Электрическое поле – силовое поле, посредством которого взаимодействуют электрические заряды.
- •Теорема Гаусса для электростатического поля:
- •Если цилиндр радиуса r имеет поверхностную плотность заряда s, а внутри его зарядов нет, то получаем:
- •Теперь изучим поведение диполя во внешнем электрическом поле. Пусть диполь помещен в однородное электрическое поле (см. Рис. 1.16).
- •Диэлектриками называют тела, не проводящие электрического тока.
- •Имеем границу раздела двух сред с и , так что, (рис. 4.10, а).
- •, Отсюда можно записать:
- •Расчет напряженности и разности потенциалов некоторых электростатических полей
- •Пример 2. Электрическое поле равномерно заряженной сферической поверхности.
- •Пример 3. Электрическое поле равномерно заряженной плоскости
- •Пример 5. Электрическое поле диполя.
- •Электроемкость уединенного проводника.
- •Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Электричество
Электростатическое
поле
– поле, создаваемое неподвижными
электрическими зарядами.
Пробный
точечный положительный заряд
(Q0)
– заряд, используемый для обнаружения
и опытного исследования электростатического
поля и не искажающий исследуемое поле
(не вызывает перераспределения зарядов,
создающих поле).
Напряженность
электростатического поля
Напряженность
поля точечного заряда
Скалярная
форма записи
Направление
вектора Е совпадает с направлением
силы, действующей на положительный
заряд. Если
поле создается положительным зарядом,
то вектор Е направлен от заряда во
внешнее пространство; если поле создается
отрицательным зарядом, то вектор Е
направлен к заряду.
Электрическое поле – силовое поле, посредством которого взаимодействуют электрические заряды.
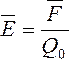 (н/Кл).
(н/Кл).  (векторная
запись)
(векторная
запись) 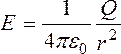 .
.
Тело, находящееся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа Работа консервативных сил совершается за счет убыли потенциальной энергии.

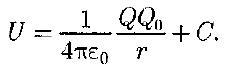
Потенциальная энергия U определяется с точностью до постоянной С. Значение постоянной обычно выбирается так, чтобы при удалении заряда на бесконечность (r → ∞) потенциальная энергия обращается в нуль ( U = 0), тогда С = 0 и потенциальная энергия заряда Qo, находящегося в поле заряда Q на расстоянии r от него, равна

Если поле создается системой n точечных зарядов Q1, Q2,..., Qn, то работа электростатических сил, совершаемая над зарядом Qo, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Qo, находящегося в этом поле, равна сумме потенциальных энергий Ui каждого из зарядов:
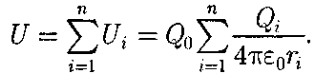
Из формул вытекает, что отношение U/Qo не зависит от Qo и является энергетической характеристикой электростатического поля, называемой потенциалом:

Потенциал поля, создаваемого точечным зарядом Q, равен

Тогда
![]()
С другой стороны

Следовательно:
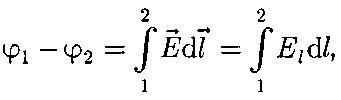
Если перемещать заряд Qо из произвольной точки за пределы поля, т. е. на бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля равна
![]()
Откуда

Потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля на бесконечность.
Единица потенциала и разности потенциалов — вольт (В): 1 В — потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж.
Потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:

-
Теорема Гаусса для электростатического поля:
поток вектора напряженности поля через любую замкнутую поверхность равен полному заряду внутри этой поверхности, деленному на e0 .
В интегральной форме:
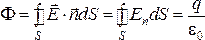 ,
(23.15)
,
(23.15)
где q − суммарный заряд внутри поверхности S.
Их расположение внутри поверхности не играет никакой роли. Заряды, расположенные вне замкнутой поверхности S не вносят вклада в поток F, ибо, сколько силовых линий входит в замкнутую поверхность, столько этих линий и выходит.
Рассмотрим некоторые важные примеры.
а). Поле бесконечной равномерно заряженной плоскости.
Пусть
плоскость заряжена равномерно с
поверхностной плотностью заряда s
(Кл/м2).
Вектор напряженности электрического
поля перпендикулярен плоскости и нормали
![]() к
ней.
к
ней.
Поскольку
поле вверх или вниз одинаково, а поток
через боковую поверхность равен 0 (из-за
того, что вектор
![]() перпендикулярен
нормали к этой поверхности), имеем:
перпендикулярен
нормали к этой поверхности), имеем:
 .
.
Сократим на ΔS:
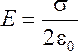 .
(23.16)
.
(23.16)
б) Поле бесконечного равномерно заряженного цилиндра (нити) с линейной плотностью заряда t
В силу симметрии вектор напряженности электрического поля направлен радиально, т. е. перпендикулярно к оси нити (см рис.).
Следовательно, для определения поля добно выбрать цилиндрическую поверхность с осью, совпадающей с осью нити. Используя теорему Гаусса, имеем:
 .
.
где h − длина выбранной цилиндрической поверхности.
