12.3 Модель Баклея – Леверетта

Задача двофазної фільтрації без урахування капілярних сил відома як задача (модель) Баклея – Леверетта. Цю модель для випадку одновимірної фільтрації одержуємо з рівняння (12.39) за , тобто

(12.48)

або

.

Рівняння (12.48) належить до класу квазілінійних рівнянь першого порядку, які звичайно розв’язуються методом характеристик.

Вперше цю модель запропонували С.Баклей і М.Леверетт 1942 року для одновимірного витіснення нафти водою без урахування сил гравітації () у вигляді (рівняння Баклея-Леверетта):

(12.49)

або

,

чи

, (12.50)

де ;.

У цьому рівнянні змінні  і  мають фізичний зміст безрозмірних об’ємів і називаються відповідно просторовою та часовою змінними.

Незалежні змінні  і , які визначаються із формул (12.38) і (12.41) відповідно для прямолінійно-паралельного і плоско-радіального потоків, можна подати в єдиній формі для цих одновимірних потоків і поширити на загальний випадок, коли сумарна „питома” витрата q фаз залежить від часу, тобто

;, (12.51)

де L – характерний лінійний розмір; n – параметр, причому n = 1 для прямолінійно-паралельного потоку і n = 2 для плоско-радіального потоку, а для останнього випадку x = r i L = R_к; r – відстань від центра нагнітальної свердловини до розглядуваної точки пласта; R_к – радіус контура пласта; q(t) = v(t) і q(t) = Q(t) / (2πh) відповідно для прямолінійно-паралельного і плоско-радіального потоків; v(t) – сумарна швидкість фільтрації фаз; Q(t) – сумарна об’ємна витрата фаз; m – коефіцієнт пористості пласта; h – товщина пласта.

Таке подання змінних  і  дає змогу поширювати рівняння (12.50) і його розв’язки на прямолінійно-паралельний і плоско-радіальний потоки.

Функцію , як уже вказувалося, називаютьфункцією Баклея-Леверетта, або функцією розподілу потоків фаз. Її фізичний зміст пояснюється так. Якщо домножити чисельник і знаменник у рівнянні (12.37) на (нагадаємо, що капілярні сили не враховуються), то дістанемо:

, (12.52)

звідки

, (12.53)

або

, (12.54)

тобто дорівнює частці витіснювальної рідини (води) в потоці.

Типовий графік функції і її похідноїпоказано на рис. 12.1,б. Залежність функцій івід відношеннядинамічних коефіцієнтів в’язкостей води і нафти подано на рис. 12.3 (див. також рис. 12.1,б, пунктирні лінії). Характерною особливістю графіка є наявність точки перегинуs_п з ділянками вгнутості і випуклості.

З використанням функції Баклея-Леверетта знаходимо швидкість фільтрації води v₁ відповідно для прямолінійно-паралельного і плоско-радіального потоків

;, (12.55)

а швидкість фільтрації нафти

. (12.56)

Для розрахунку параметрів двофазного потоку до рівняння (12.50) треба додати початкову та граничну умови:

(12.57)

Перша умова (12.54) означає, що в початковий момент часу (), тобто до початку процесу витіснення в пласті мав місце відомий розподіл насиченостіs водою, що описується функцією . Можна було б задатичи. Друга умова (12.54) означає, що на початку пласта (), тобто на лінії водонагнітальної галереї, за часунасиченість водою зростає, що описується функцією, хоч те ж можна задати.

У процесі витіснення нафти водою насиченість s в якій-небудь фіксованій точці пласта змінюється з часом. Разом з тим точки, в яких насиченість дорівнює якій-небудь фіксованій значині(точніше площина), переміщуються з часом у напрямі руху рідини. Цю насиченістьs = const називають характеристикою рівняння (12.50) (метод розв’язування називають методом характеристик). У такому розумінні рівняння (12.50) є рівнянням руху площини з постійною насиченістю. Для визначення швидкості руху площини з постійною насиченістю можна записати:

, (12.58)

або

, (12.59)

звідки

, (12.60)

оскільки .

Із рівняння Баклея – Леверетта (12.50) маємо:

. (12.61)

Прирівнюючи рівняння (12.60) і (12.61), дістаємо рівняння швидкості переміщення площини з постійною насиченістю:

або

. (12.62)

Із рівняння (12.60) записуємо

,

а підставивши в рівняння Баклея – Леверетта (12.50), доходимо знову до рівняння (12.62), тобто еквівалентною рівнянню (12.50) в частинних похідних є система звичайних диференціальних рівнянь першого порядку (12.58) і (12.62), які називаються умовами на характеристиках.

Формальний розв’язок цієї системи рівнянь (12.58) і (12.62) за початкової і граничної умов (12.57) або розв’язок рівняння (12.62) для характеристики , що є розв’язком рівняння (12.58), можна записати:

(12.63)

або за

, (12.64)

де – початковий розподіл насиченості для(еквівалентно першому рівнянню умови (12.57)).

Задаючись значинами , із рівняння (12.64) визначаємо координату  , де насиченість становить величину s.

Профіль насиченості зручно подати у вигляді залежності насиченості s від безрозмірної просторової координати:

, (12.65)

де – об’єм частини пласта, що обмежується координатоюх; – сумарний об’єм води, що увійшла в пласт.

Тоді в кінцевому підсумку розв’язок (12.64) записуємо так:

. (12.66)

Для безпосереднього розрахунку, маючи експериментальні залежності відносних коефіцієнтів проникностей івід насиченості пор водоюs (див. рис. 12.1, а), можна, використовуючи вираз (12.37), побудувати спочатку функцію , потім графічним диференціюванням –(див. рис. 12.1,б). Оскільки , то відповідно відразу маємо графік розподілу насиченостіs уздовж координати  (див. рис. 12.1, в), що ідентичний графіку рис. 12.1, б.

Із рис. 12.1, в видно, що насиченість s у кожній точці пласта і в кожний момент часуt є двозначною. Фізично це є абсурдом – у кожній точці в кожний момент часу має існувати тільки одна цілком визначена насиченість. Звідси випливає, що залежність насиченості s від координати  справедлива тільки до деякої значини і длязначина насиченостіs має змінюватися стрибком від до, деs_з в – вміст (насиченість) зв’язаної води; s_ф – насиченість водою в точці .

Отже, для усунення двозначності припускаємо існування стрибка насиченості (s - стрибок) і вводимо поняття фронту витіснення, а безрозмірна координата є координатою фронту витіснення, причому

. (12.67)

Можна показати, що насиченість пор водою на фронті витіснення

(12.68)

звідки

. (12.69)

Співвідношення (12.69) виражає тангенс кута нахилу дотичної, проведеної з точки , до кривої, тоді абсциса точки дотику Д дорівнює насиченості водоюs_ф на фронті витіснення.

Графічно безрозмірну координату і насиченість водою на фронтіs_ф можна визначити з умови рівності площ, заштрихованих на рис. 12.1, в горизонтальними лініями. Зазначаємо, що на рис. 12.1, в s_н і s_н ф означають насиченості породи рухомою нафтою в зоні витіснення (у водонафтовій зоні) і на фронті витіснення.

Фізичною особливістю моделі Баклея-Леверетта є залежність швидкості поширення площини з насиченістюs від величини тієї ж насиченості s згідно з рівнянням (12.59). Таке явище називається дисперсією хвиль (нагадаємо, що дисперсія – це розсіяння, подрібнення). Так, у рівнянні (12.59) є функцієюs. Як видно з рис. 12.2, б чи 12.3, функція зростає за, а значить, площини більших насиченостей поширюються з більшими швидкостями, деs_п – точка перегину графіка з ділянками вгнутості і випуклості. Завідповідно швидкість поширення площини постійної насиченості починає зменшуватися (зменшується). Тобто, як видно з початкового розподілу насиченостіза = 0 з перебігом часу  нахил профілю розподілу насиченості стає щораз крутішим, оскільки більші значини насиченості „наздоганяють” менші значини і в деякий момент відбувається „перекидання” хвилі насиченості, а графікстає неоднозначним (рис. 12.4). Така неоднозначність і усувається введенням стрибка насиченості. Стрибок насиченості виникає і поширюється, починаючи з моменту часу_*, коли дотична до кривої стає вертикальною. Неоднозначність графікапоказано ділянкою кривої 1 - 2 - 3 - 4 - 5 на рис. 12.4, де одному і тому ж_ф відповідає три значини насиченості: s₁, s₂, s₃. Величина стрибка визначається відрізком 1 - 3 - 5.

Якщо в початковий момент часу за насиченість, тобто є постійною вздовж координати, причому (слабко обводнений пласт або насичений тільки нафтою заs₀ = 0), то виникає стрибок насиченості (рис. 12.5, а). Якщо ж за таких же умов (високообводнений пласт), то стрибок насиченості відсутній (див. рис. 12.5,б).

Розв’язок задачі має вигляд для випадку

за = 0,   0;

за 0<   _ф,   0;

за_ф <   1,   0

і для випадку

за = 0,   0;

за 0<  < ,   0;

за<  < 1,   0,

де – координата фронту витіснення;s_ф, s₀, s_з в – насиченість водою на фронті витіснення, початкова водонасиченість пласта (зокрема s₀ = 0, s₀ = s_з в, s₀ > s_з в) і насиченість зв’язаною водою.

Середня водонасиченість s_с у зоні витіснення до прориву води із пласта дорівнює коефіцієнту нафтовилучення, точніше коефіцієнту витіснення , який подаємо так:

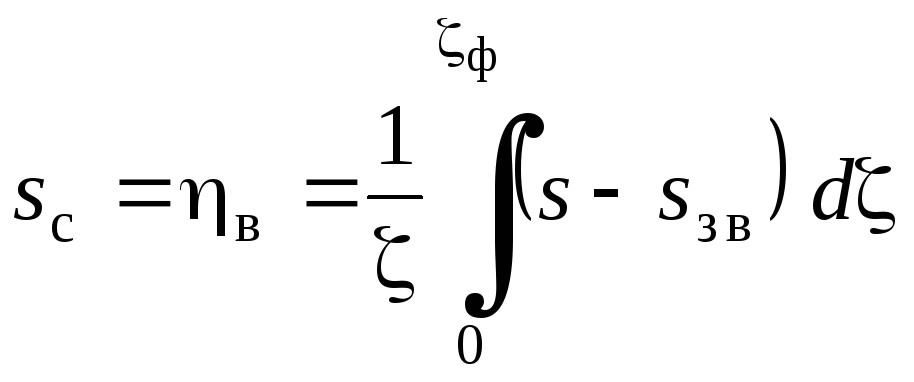. (12.70)

Нагадуємо, що коефіцієнт нафтовилучення – це відношення кількості відібраної нафти до початкового запасу в покладі, акоефіцієнт витіснення – це відношення об’єму нафти, витісненої з області пласта, що зайнята водою, до початкового об’єму нафти у цій самій області. Рівність об’ємів запомпованої в пласт води і витісненої звідти нафти записуємо так:

,

звідки

, (12.71)

тобто інтеграл у рівнянні (12.71) (площа, заштрихована на рис. 12.1, в вертикальними лініями) дорівнює одиниці. Тут V_ф – об’єм пласта в зоні витіснення, а . Тоді

, (12.72)

або

. (12.73)

Вираз (12.73) має таку геометричну інтерпретацію. Якщо продовжити дотичну до кривої f (s) (див. рис. 12.1, б), яка визначає насиченість s_ф на фронті витіснення, до перетину в точці П з горизонтальною прямою f (s) = 1, то абсцисса точки П визначає середню водонасиченість s_с в зоні витіснення, причому s_с = η_в.

Коефіцієнт безводного нафтовилучення записуємо так:

. (12.74)

Чисельник у рівнянні (12.74) інтегруємо частинами і знаходимо:

, (12.75)

де враховано, що із виразу (12.64),,– найбільша (максимальна) водонасиченість на лінії нагнітання води.

Оскільки за рівнянням (12.67)

(12.76)

та із рівняння (12.66)

, (12.77)

то підставляючи рівняння (12.75) у рівняння (12.74), знаходимо коефіцієнт безводного нафтовилучення

або

. (12.78)

Звідси, враховуючи рівняння (12.37), виснуємо, що коефіцієнт безводного нафтовилучення збільшується із зростанням співвідношення динамічних коефіцієнтів в’язкостей (див. рис. 12.1,б і в, пунктирні лінії), тобто зі збільшенням динамічного коефіцієнта в’язкості витіснювальної фази (води) і (або) зі зменшенням динамічного коефіцієнта в’язкостівитіснюваної фази (нафти).

Для наочності розподіл насиченості водою s вздовж координати х на різні моменти часу t, причому , показано на рис. 12.6, оскільки.

Отже, для графічного розрахунку процесу витіснення нафти водою необхідно:

а) побудувати графік функції Баклея-Леверетта f(s) за рівнянням (12.37), задаючи відношення μ_о динамічних коефіцієнтів в’язкостей фаз (води і нафти) та відносні коефіцієнти фазових проникностей води і нафти як функції коефіцієнта насиченості водою s (у вигляді експериментальних графіків чи емпіричних формул);

б) провести дотичну із точки s = s_зв до кривої f(s) і за точкою дотику Д (див. рис. 12.1, б) як абсцису її визначити насиченість водою s_ф на фронті витіснення та як ординату – значину функції Баклея-Леверета f(s_ф) на фронті витіснення;

в) за точкою П перетину даної дотичної з горизонтальною прямою f(s) = 1 визначити середню водонасиченість s_с в зоні витіснення, яка дорівнює коефіцєінту витіснення η_в;

г) безрозмірну координату ζ_ффронту витіснення розрахувати за формулою (12.67) або із формули (12.72), причомуf(s_зв) = 0;

д) безрозмірну просторову координату визначити за формулою ξ_ф = ζ_фτ, а розмірну просторову координату x чи r – з використанням формул (12.51). Так, для прямолінійно-паралельного потоку маємо: , деQ_Σ = Qt – сумарний об’єм запомпованої в пласт води; Q – об’ємна витрата води; t – час; m – коефіцієнт пористості пласта; F – площа фільтрації;

е) коефіцієнт безводного нафтовилучення за формулою (12.78).

Для аналітичного розрахунку процесу витіснення нафти водою необхідно:

а) задати (чи підібрати) аналітичні залежності відносних коефіцієнтів фазових проникностей води і нафти як функцій коефіцієнта насиченості водою s;

б) розв’язати нелінійне рівняння (12.69) відносно s_ф, тобто визначити коефіцієнт насиченості водою s_ф на фронті витіснення в системі MathCAD з допомогою фукції root;

в) розрахувати функцію Баклея-Леверетта для визначеного коефіцієнта насиченості водою f(s_ф);

г) із рівняння дотичної прямої лінії , яка проходить через дві точки з координатами [f(s_зв),s_зв] і [f(s_ф),s_ф], визначити коефіцієнт середньоїнасиченостіs_сводою в зоні витіснення як точку перетину дотичної прямої лінії з горизонтальною прямою лінієюf(s) = 1, тобто

,

де f(s_зв) = 0;

е) аналогічно попередньому розрахунку визначити безрозмірну координату ζ_ф, безрозмірну координату ξ_фі розмірну просторову координатуx чи r для заданого моменту часуtвід початку процесу витіснення, коефіцієнт безводного нафтовилучення.

Задача 12.1. У пористому пласті має місце прямолінійно-паралельне витіснення нафти водою за законом Дарсі. Визначити величини коефіцієнта фронтової насиченості порового простору водою і координати фронту витіснення на момент часу t = 30 діб. Відомо: товщина пласта і ширина фільтраційного потоку h = 15 м і B = 400 м; довжина галереї L = 800 м; коефіцієнт пористості пласта m = 14%; дебіт галереї Q = 240 м³/доб (за пластових умов); динамічні коефіцієнти в’язкості нафти і води μ_н = 3 мПас і μ_в = 1 мПас. Відносні коефіцієнти фазових проникностей води і нафти задаються умовами:

де s – коефіцієнт водонасиченості пор.

Розв’язування. Для розв’язування використовуємо машинну програму в системі MathCAD. Відносні коефіцієнти фазових проникностей для води і нафти описується рівняннями:

Будуємо графіки залежностей відносних коефіцієнтів фазових проникностей від коефіцієнта водонасиченості s, для чого задаємо послідовний ряд значин кефіцієнта водонасиченості від 0 до 1 з кроком 0,01 (в системі MathCAD s = 0,0,01..1) (аналогічно графікам на рис. 12.1, а).

Розраховуємо функцію розподілу потоків фаз за формулою:

,

де – відношення динамічних коефіцієнтів в’язкостей води і нафти,

,

а відтак будуємо графік розподілу потоків фаз (функцію Баклея–Леверетта) від коефіцієнта водонасиченості f(s) (аналогічно графіку на рис. 12.1, б).

Для графічного визначення насиченості пор водою на фронті витіснення проводимо дотичну із точки s = s_зв = 0,2 до кривої f(s). За точкою дотику як абсцису визначаємо коефіцієнт насиченості водою на фронті витіснення s_ф = 0,59, а як ординату – значину функції Баклея–Леверетта f(s_ф) = 0,87.

За точкою перетину даної дотичної з горизонтальною прямою f(s) = 1 як абсцису визначаємо коефіцієнт середньої водонасиченості s_с = 0,64 в зоні витіснення, яка дорівнює коефіцієнту витіснення η_в.

Визначаємо безрозмірну координату фронту витіснення за формулою:

2,231,

причому f(s_зв) = 0.

Визначаємо безрозмірну просторову координату за формулою:

ξ_ф = ζ_ф τ ,

де τ =0,0107;Q – об’ємна витрата води, м³/доб; t – час, доб; m – коефіцієнт пористості пласта; F = Bh – площа фільтрації, м², тобто:

ξ_ф = 2,231·0,0107 = 0,02387.

Розмірну просторову координату фронту витіснення розраховуємо за формулою:

19,120 м,

де Q t – сумарний об’єм запомпованої в пласт води, м³.

Визначаємо коефіцієнт безводного нафтовилучення за формулою:

0,560.

Для аналітичного розрахунку процесу витіснення нафти водою використовуємо нелінійне алгебраїчне рівняння , яке розв’язуємо відносноs_ф. Для визначення коефіцієнта насиченості водою s_ф на фронті витіснення перетворюємо дане рівняння до вигляду , для чого похідну виражаємо (у машинній програмі MathCAD) так.

Використовуючи команду root у машинній програмі MathCAD, визначаємо s_ф, для чого задаємо дві граничні значини області водонасиченості, в якій існує шукана значина s_ф:

0,59009,

де 0,3 та 0,8 – граничні значини можливої області існування s_ф; s_ф = 0,59009.

Розраховуємо значину функції Баклея–Леверетта:

0,86998.

Із рівняння дотичної прямої лінії , яка проходить через дві точки з координатами [f(s_зв), s_зв] і [f(s_ф), s_ф], визначаємо коефіцієнт середньої насиченості водою в зоні витіснення як точку перетину дотичної лінії з горизонтальною прямою лінією f(s) = 1, тобто

0,64839,

де f(s_зв) = 0.

Аналогічно попередньому розрахунку визначаємо координату ζ_ф == 2,223, ξ_ф = 2,223·0,0107 = 0,0239, а потім і координату фронту витіснення нафти водою x_ф =19,143 м на момент часу t = 30 діб.

Відповідь: коефіцієнт фронтової насиченості s_ф = 0,59009; координата фронту витіснення х_ф = 19,143 м.

12.4 Модель Раппопорта – Ліса

Модель двофазної фільтрації з урахуванням капілярних сил називають моделлю Раппопорта – Ліса. Для одновимірного витіснення нафти водою без урахування сили гравітації таку модель запропонували Л.Раппопорт і В.Ліс 1953 року (рівняння Раппопорта – Ліса), тобто

. (12.79)

Якщо в моделі Баклея – Леверетта капілярні сили побічно враховуються через коефіцієнти фазових проникностей, то в моделі Раппопорта – Ліса стрибок капілярного тиску задається у вигляді експериментальної функції насиченості (функції Леверетта).

Модель Баклея – Леверетта, враховуючи фазові проникності для нафти і води, які певним чином залежать від капілярних сил, все-таки не дає змоги описати процеси фільтрації незмішуваних рідин, коли сам рух рідин зумовлюється дією капілярних сил.

Дія капілярних сил проявляється в основному поблизу фронту витіснення, де градієнти насиченості дуже великі. Аналіз показує, що капілярні сили “розмазують” фронт, тому в разі їх урахування стрибок насиченості відсутній, а насиченість водою змінюється безперервно до насиченості зв’язаною водою.

Експериментами було виявлено, що за постійної швидкості витіснення розподіл насиченості в перехідній зоні поблизу фронту витіснення не змінюється в часі, тобто утворюється так званастабілізована зона. Вона переміщається, не змінюючи своєї форми. Рух у стабілізованій зоні відповідає граничному розв’язку рівняння (12.76), коли розподіл насиченості не залежить від граничних умов. Розподіл насиченості у стабілізованій зоні є усталеним (рис. 12.7), тобто не залежить від часу. Позаду стабілізованої зони розподіл насиченості описується моделлю Баклея – Леверетта.

Знайдемо розв’язок рівняння (12.76) стосовно прямолінійно-паралельного потоку. Вводимо швидкість руху фронту витіснення . Робимо заміну змінних

, (12.80)

а відтак шукаємо розв’язок (12.76) у вигляді:

. (12.81)

Відповідно до цього перетворюємо рівняння (12.79), знайшовши із рівняння (12.81) з урахуванням рівняння (12.80) величини:

, (12.82)

тобто

. (12.83)

Інтегруючи рівняння (12.83) по u, отримуємо:

, (12.84)

де с – постійна інтегрування.

Оскільки позаду стабілізованої зони зміна насиченості описується моделлю Баклея-Леверетта, а рух у перехідній зоні є усталеним з координатою u, то граничні умови мусять бути такими:

, (12.85)

де s_ф і s₀ – насиченості відповідно за і перед стрибком насиченості, які пов’язані між собою співвідношенням (12.67), причому .

Тоді із рівняння (12.84) знаходимо постійну інтегрування

, (12.86)

а друга умова (12.85) виконується автоматично, так як s_ф і s₀ пов’язані між собою.

Із рівняння (12.84) з урахуванням виразу (12.86) знаходимо

(12.87)

Проінтегрувавши рівняння (12.87) по u від u₁ до u та відповідно по s від s₁ до s, де , і врахувавши, що, отримуємо розв’язок рівняння (12.79) у вигляді:

. (12.88)

Рівняння (12.88) описує розподіл насиченості в перехідній зоні нескінченної довжини, що є наслідком умов (12.85), а значить відсутні точки змикання отриманого розв’язку з розподілом Баклея-Леверетта.

Якщо взяти значини насиченостей не рівні s_ф і s₀, а близькі до них, то виявляється, що ширина перехідної зони є пропорціональною величині

(12.89)

або

. (12.90)

Зауважуємо, що рівняння (12.76) має також, окрім розв’язку (12.88), точні автомодельні розв’язки, які існують за спеціально вибраної сумарної швидкості фільтрації .

Модель Раппопорта – Ліса дає змогу описати процеси фільтрації незмішуваних рідин, коли сам рух рідин зумовлений дією капілярних сил, зокрема процеси прямоплинного та протиплинного капілярного просочування (рис. 12.8).

У разі протиплинного капілярного просочування нафта у взірці гідрофільного пористого середовища, який занурено у воду, під дією капілярних сил заміщається водою, причому рух їх відбувається в протилежних напрямах. Вода входить дрібними порами, а нафта виходить більшими порами, вспливаючи на поверхню води.

У разі прямоплинного капілярного просочування насичений нафтою взірець гідрофільного пористого середовища всмоктує воду з одного кінця, а нафта виходить із взірця через другий кінець. Відзначаємо, що може спостерігатися і комбіноване (прямоплинно - протиплинне) просочування.

Виникає питання про області застосування моделей Баклея – Леверетта та Раппопорта – Ліса. Область застосування моделі Баклея – Леверетта одержується із моделі Раппопорта – Ліса, коли . Величинуназиваютькапілярним числом (зазначимо, що відомо багато різних записів капілярного числа). Оскільки

,

то величина в першу чергу визначається характерним розміромL області фільтрації. Оцінимо величину капілярного числа . Беремо: = 25 мН/м (для нафти і води); cos  = 1; ₂ = 2,5 мПас; т = 0,1; k = 10^-13 м²; v = 10^-5 м/с. Тоді

.

Якщо L = 0,1 м (лабораторний керн чи фронт витіснення), то  1, а в разі L = 10² – 10⁴ м (відстань між свердловинами в пласті) = 10^-3 – 10^-5. Тобто в разі великомасштабного розгляду двофазної фільтрації між свердловинами можна нехтувати капілярними силами і брати модель Баклея – Леверетта. Для вивчення розподілу насиченості на фронті витіснення необхідно врахувати капілярні сили, використовуючи модель Раппопорта – Ліса. Звідси випливає, що загально використовувана теорія двофазної фільтрації, в основі якої лежить модель Баклея – Леверетта, є асимптотичною теорією, бо відповідає малим значинам капілярного числа.

Силою гравітації (ваги) можна нехтувати, якщо , оскільки гравітаційне число , то цьому відповідає умова.