Задачи для самостоятельного решения

1. Показать, что векторное поле является потенциальным и найти его потенциал.

2. Показать, что векторное поле

является потенциальным и найти его потенциал.

Ответы

1.  .

2.  .

Соленоидальное поле

Пример. Индукция магнитного поля, созданного электрическим током в проводе, расположенным вдоль оси , определяется формулой

.

Показать, что это поле соленоидально, и найти один из его векторных потенциалов.

Решение. Убедимся сначала в соленоидальности поля, то есть в том, что его дивергенция равна нулю.

.

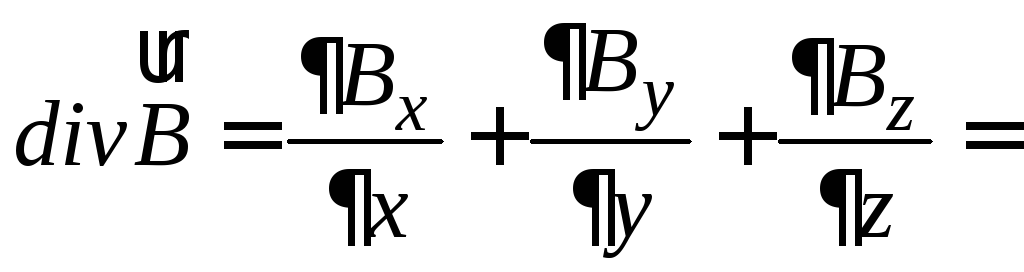
Наше поле задано во всем пространстве кроме точек, расположенных на оси . Пространство с выколотой осьюявляется обьемно-односвязной областью. Действительно, любая замкнутая поверхность в нем ограничивает область, целиком лежащую в этом пространстве. Значит, наше поле обладает векторным потенциалом. Ротор векторного потенциала во всех точках области совпадает с индукцией магнитного поля, то есть выполняются три уравнения

, ,.

Векторный потенциал определяется с точностью до градиента произвольного скалярного поля, поэтому положим. Тогда из третьего уравнения имееми. Из первого уравненияполучаем

.

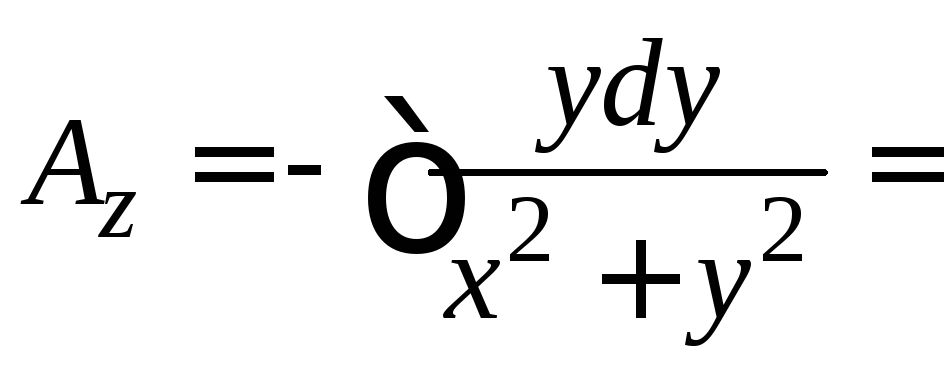
Находим частные производные ,и, подставляя их во второе уравнение, видим, что функциииудовлетворяют условию. Полагаем их равными нулю и находим один из векторных потенциалов.

Задачи для самостоятельного решения

3. Показать, что векторное поле соленоидально, и найти один из его векторных потенциалов.

4. Определить соленоидальность напряженности электрического поля точечного заряда, расположенного в начале координат .

5. Определить соленоидальность напряженности электрического поля равномерно заряженного по объему диэлектрического шара, расположенного в начале координат .

Ответы

3.  .

4.  Соленоидально.

5.  Не соленоидально.

32