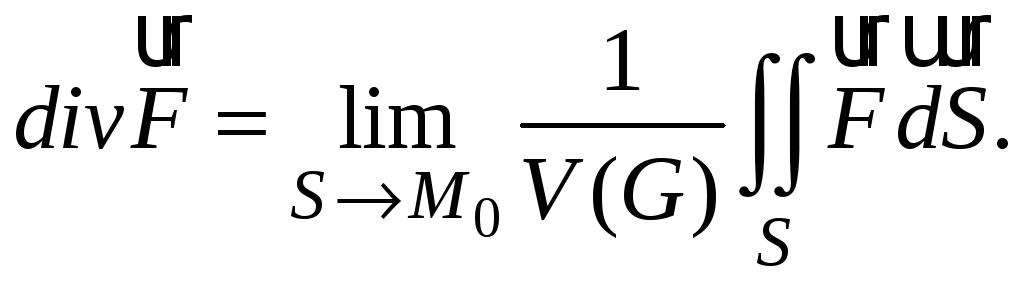- •Криволинейный интеграл второго рода
- •Лекции 34-35. Поверхностные интегралы. Существование и вычисление. Площадь поверхности, заданной параметрически. Формулы Стокса и Гаусса-Остроградского.
- •Литература к лекции 34-35
- •Лекция 36. Элементы теории поля. Потенциальное и соленоидальное поля. Оператор Гамильтона.
Модуль 6
«Криволинейные, поверхностные интегралы. Элементы теории поля»
дисциплины
«Математический анализ»
Содержание лекционного материала
Лекция 33. Криволинейные интегралы 1-го и 2-го рода. Существование и вычисление. Формула Грина. Применение.
Основные понятия: скалярное поле, векторное поле, криволинейный интеграл.
П усть
в некоторой пространственной области
задано скалярное поле
усть
в некоторой пространственной области
задано скалярное поле
![]() ,
а также кусочно-гладкая кривая
,
а также кусочно-гладкая кривая
![]() :
:
![]() .
Разобьем кривую
.
Разобьем кривую
![]() любым образом на n
“элементарных дуг” длиной
любым образом на n
“элементарных дуг” длиной
![]() ,
в произвольном месте каждой элементарной
дуги возьмем по точке Mk
.
Составим интегральную сумму:
,
в произвольном месте каждой элементарной
дуги возьмем по точке Mk
.
Составим интегральную сумму:
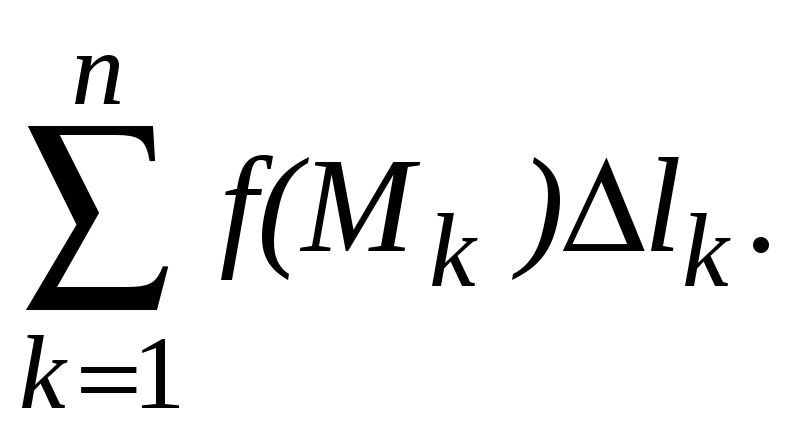 Возьмем от нее предел при стремлении
максимальной длины “элементарной дуги”
к нулю. Этот предел, если он существует
и конечен, не зависит от разбиения кривой
и выбора точек Mk
,
называется криволинейным интегралом
первого рода по кривой
Возьмем от нее предел при стремлении
максимальной длины “элементарной дуги”
к нулю. Этот предел, если он существует
и конечен, не зависит от разбиения кривой
и выбора точек Mk
,
называется криволинейным интегралом
первого рода по кривой
![]() и обозначается
и обозначается
![]() .
.
Криволинейный интеграл первого рода сводится к определенному интегралу
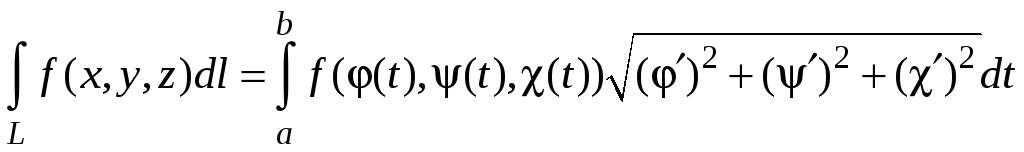 ,
,
в
котором “элементарная дуга”
![]() может принимать только неотрицательное
значение, то есть значение криволинейного
интеграла первого рода не зависит от
направления интегрирования. Криволинейным
интегралом
может принимать только неотрицательное
значение, то есть значение криволинейного
интеграла первого рода не зависит от
направления интегрирования. Криволинейным
интегралом
![]() определяется длина кривой L,
а интегралом
определяется длина кривой L,
а интегралом
![]() ,
где функцией
,
где функцией
![]() обозначена линейная плотность кривой,
определяется масса кривой L.
обозначена линейная плотность кривой,
определяется масса кривой L.
Криволинейный интеграл второго рода
П усть
в некоторой пространственной области
задано векторное поле
усть
в некоторой пространственной области
задано векторное поле![]() ,
а также кусочно-гладкая кривая L:
,
а также кусочно-гладкая кривая L:
![]() .
Ориентируем эту кривую, указав начальную
точку и конечную. Пусть
.
Ориентируем эту кривую, указав начальную
точку и конечную. Пусть
![]() –
орт касательной в точке М к кривой L,
совпадающий по направлению с направлением
кривой. Разобьем кривую L
любым образом на n
“элементарных дуг” длиной
–
орт касательной в точке М к кривой L,
совпадающий по направлению с направлением
кривой. Разобьем кривую L
любым образом на n
“элементарных дуг” длиной
![]() ,
в произвольном месте каждой элементарной
дуги возьмем по точке Mk.
Составим интегральную сумму
,
в произвольном месте каждой элементарной
дуги возьмем по точке Mk.
Составим интегральную сумму
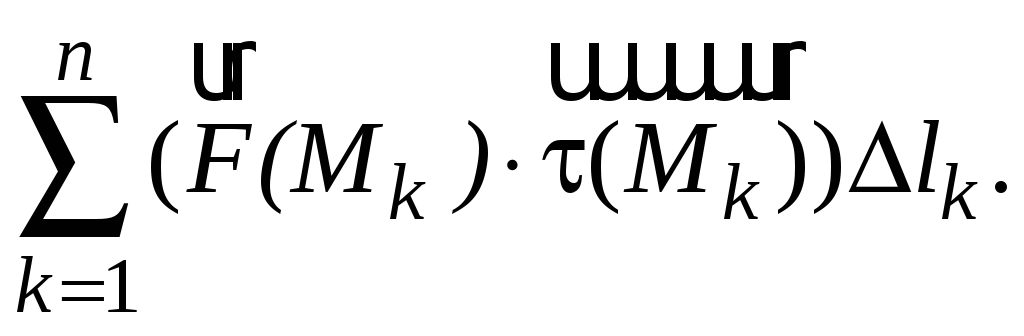 Произведение
в круглых скобках – скалярное произведение
двух векторов. Предел этой интегральной
суммы при
Произведение
в круглых скобках – скалярное произведение
двух векторов. Предел этой интегральной
суммы при
![]() называется криволинейным интегралом
первого рода от скалярного поля
называется криволинейным интегралом
первого рода от скалярного поля
![]() по кривой L:
по кривой L:
![]()
Если
ввести в рассмотрение новый вектор
![]() с
координатами
с
координатами
![]() ,
криволинейный интеграл первого рода
от скалярного поля
,
криволинейный интеграл первого рода
от скалярного поля
![]() можно записать как криволинейный
интеграл второго рода от векторного
поля
можно записать как криволинейный
интеграл второго рода от векторного
поля
![]() :
:
![]()
Криволинейный интеграл второго рода сводится к определенному интегралу:
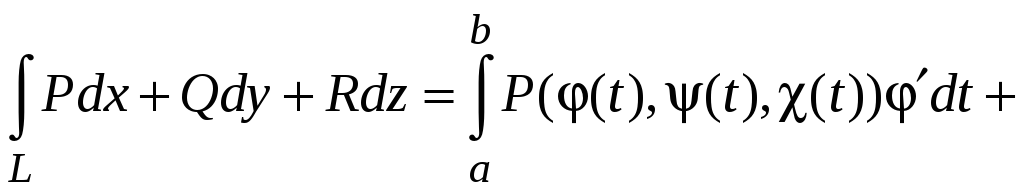
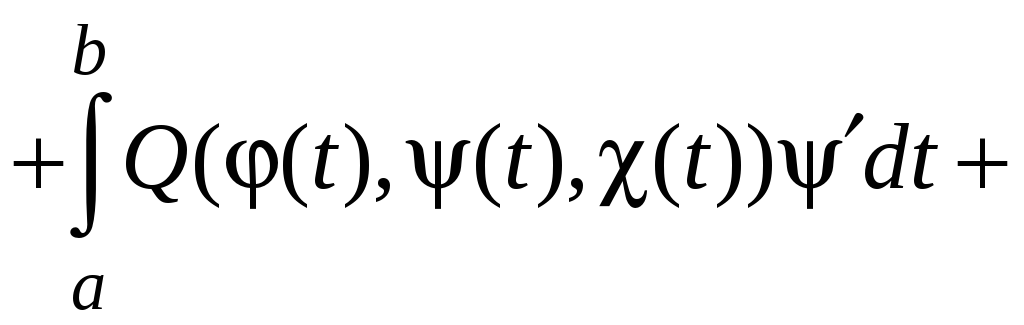
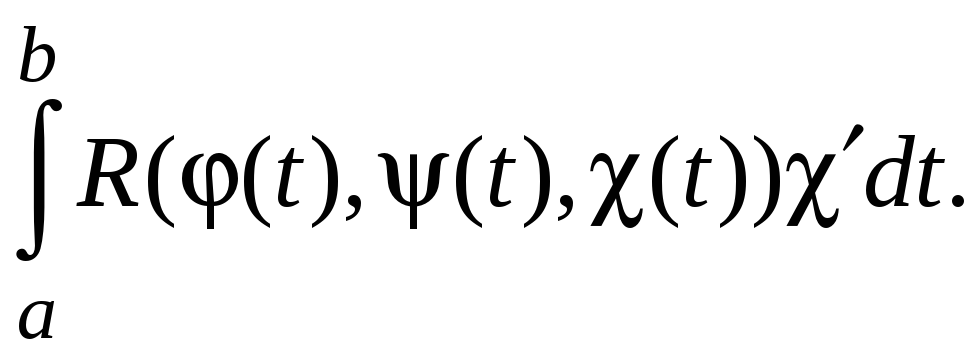
Если
векторное поле
![]() является
силой, приложенной к телу, тогда
криволинейный интеграл второго рода
будет равен работе по перемещению этого
тела вдоль кривой L.
Даже если поле
является
силой, приложенной к телу, тогда
криволинейный интеграл второго рода
будет равен работе по перемещению этого
тела вдоль кривой L.
Даже если поле
![]() не является силой, криволинейный интеграл
второго рода называют работой векторного
поля вдоль кривой L.
не является силой, криволинейный интеграл
второго рода называют работой векторного
поля вдоль кривой L.
Когда
кривая L
, по которой берется интеграл, замкнутая,
криволинейный интеграл второго рода
от векторного поля
![]() называется
циркуляцией векторного поля
называется
циркуляцией векторного поля
![]() по
замкнутой кривой L
и обозначается
по
замкнутой кривой L
и обозначается
![]()
Литература к лекции 33
1. Высшая математика: Учебник для вузов: В 3-х т. Т. 3 : Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я. С. Бугров, С. М. Никольский ; Под ред. В.А. Садовничего. - 7-е стер. изд. - М. : Дрофа, 2005. - 512 с.
Лекции 34-35. Поверхностные интегралы. Существование и вычисление. Площадь поверхности, заданной параметрически. Формулы Стокса и Гаусса-Остроградского.
-
Основные понятия: поверхностные интегралы первого и второго рода, площадь поверхности, ротор, дивергенция.
-
Пусть в некоторой пространственной области задано скалярное поле
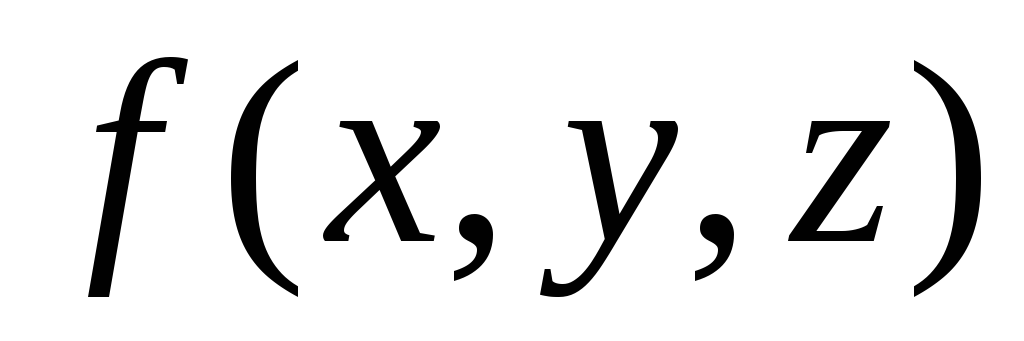 ,
а также кусочно-гладкая поверхность
,
а также кусочно-гладкая поверхность
 :
:
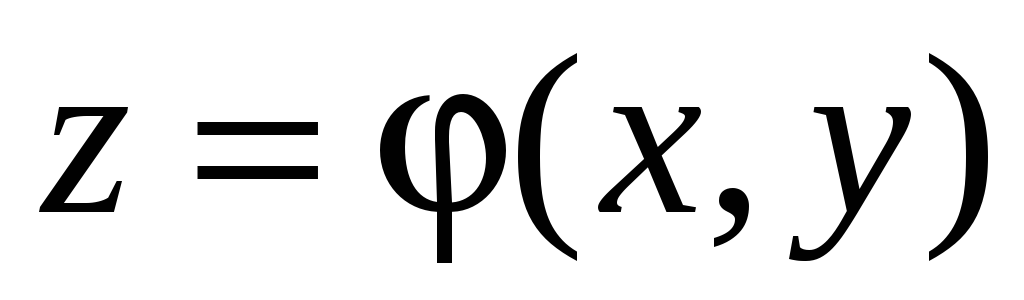 .
Разобьем поверхность
.
Разобьем поверхность
 на n
пересекающихся разве что по границе
частей.
на n
пересекающихся разве что по границе
частей.
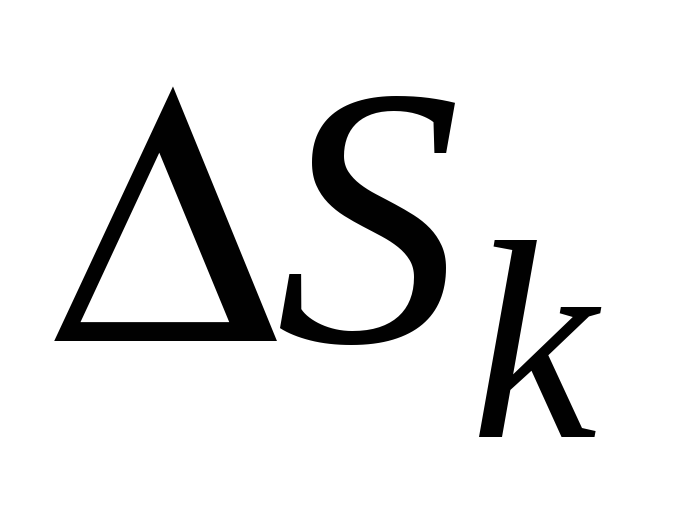 - площадь k-той
части. В каждой части выберем произвольную
точку Mk
.
Составим интегральную сумму
- площадь k-той
части. В каждой части выберем произвольную
точку Mk
.
Составим интегральную сумму
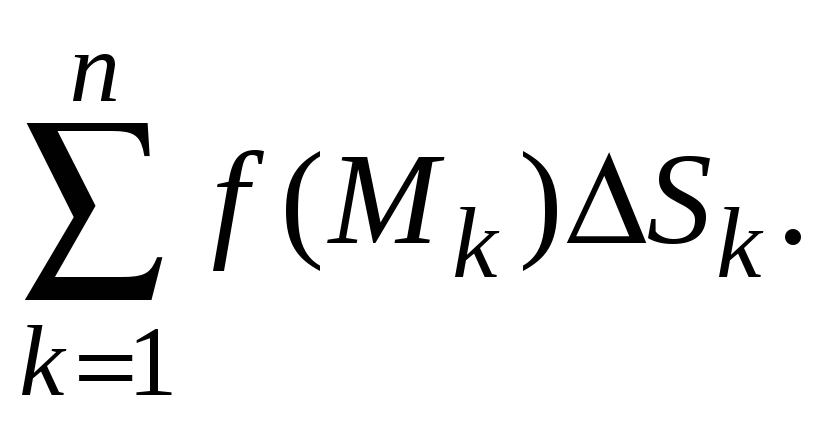 Конечный предел этой интегральной
суммы при
Конечный предел этой интегральной
суммы при
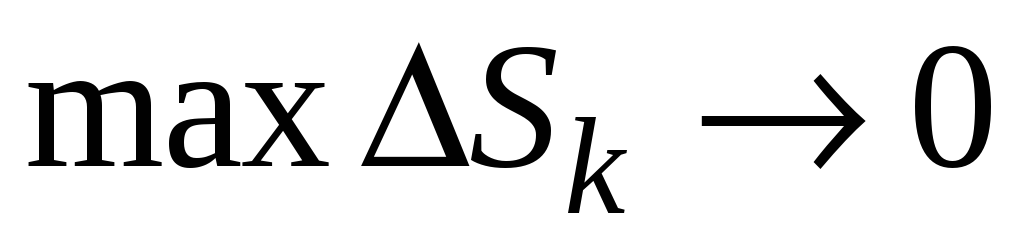 ,
если он не зависит от разбиения
поверхности и от выбора точек Mk
,
называется
поверхностным интегралом от скалярного
поля
,
если он не зависит от разбиения
поверхности и от выбора точек Mk
,
называется
поверхностным интегралом от скалярного
поля
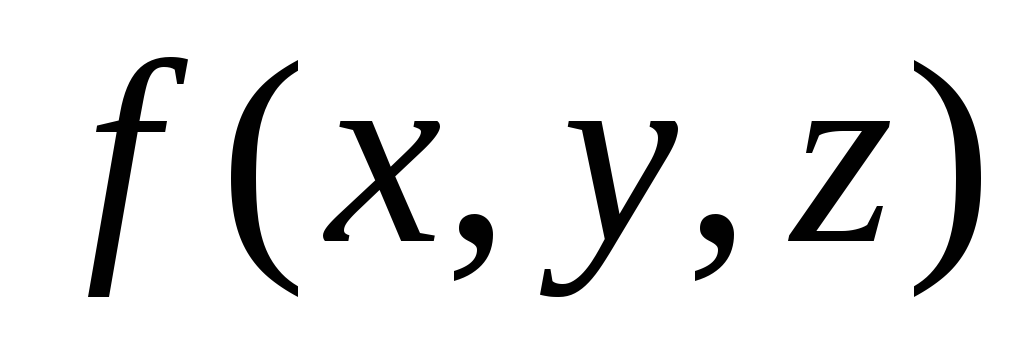 по
поверхности
по
поверхности
 :
:
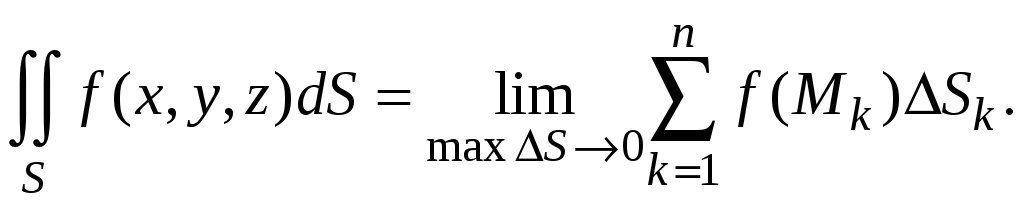
-
Спроектировав поверхность
 на плоскость
на плоскость
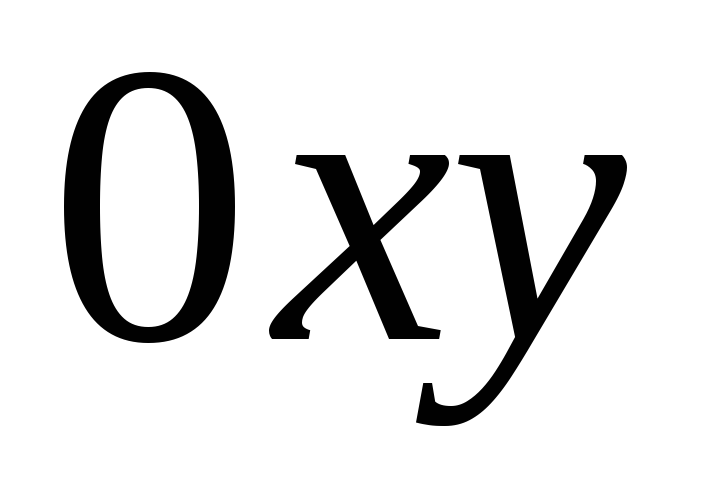 ,
поверхностный интеграл по поверхности
,
поверхностный интеграл по поверхности
 можно свести к двойному интегралу по
проекции
можно свести к двойному интегралу по
проекции
 - по плоскому множеству
- по плоскому множеству
 :
:
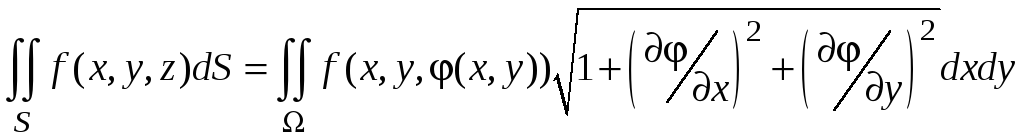 .
.
-
Пусть в некоторой пространственной области задано векторное поле
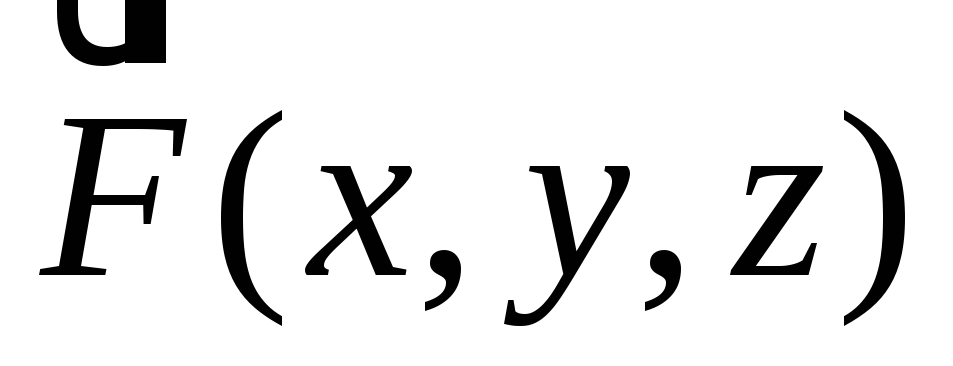 ,
а также кусочно-гладкая поверхность
,
а также кусочно-гладкая поверхность
 ,
которую можно описать одним из уравнений:
,
которую можно описать одним из уравнений:
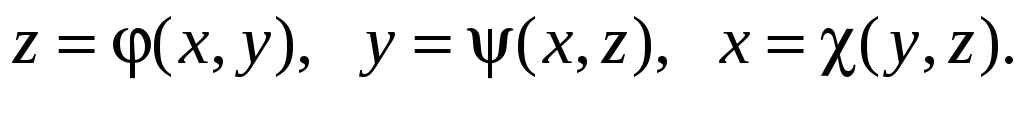 Пусть
Пусть
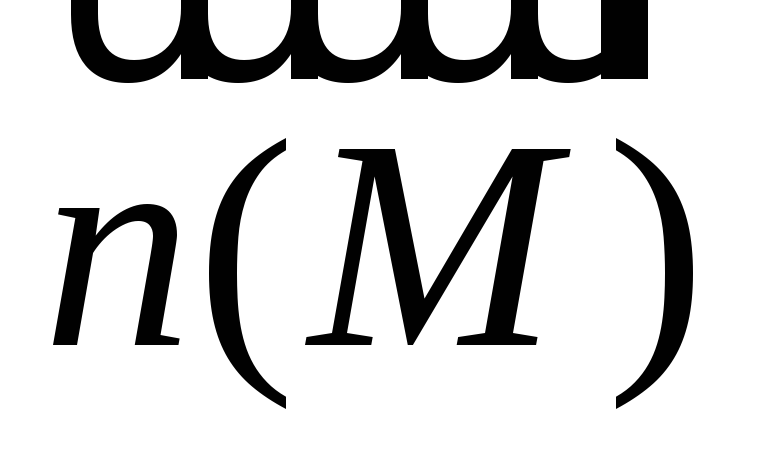 -
единичный вектор нормали на выбранной
стороне поверхности. Разобьем поверхность
-
единичный вектор нормали на выбранной
стороне поверхности. Разобьем поверхность
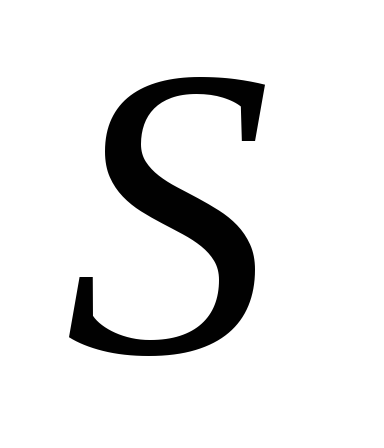 на n
пересекающихся разве что по границе
частей.
на n
пересекающихся разве что по границе
частей.
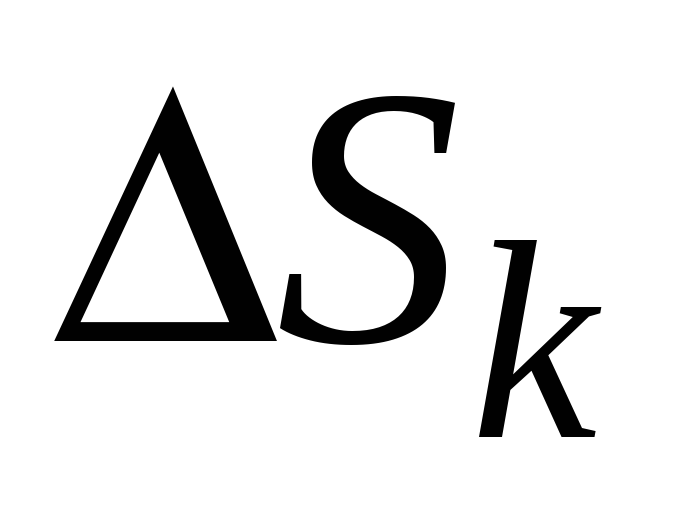 - площадь k-той
части. В каждой части выберем произвольную
точку
- площадь k-той
части. В каждой части выберем произвольную
точку
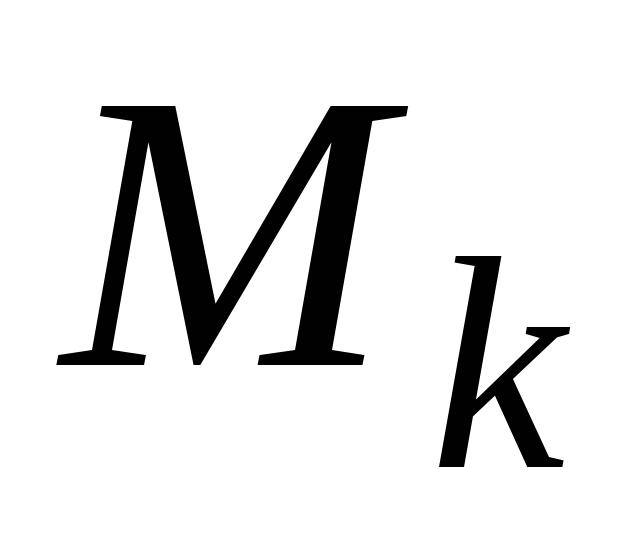 .
Составим интегральную сумму
.
Составим интегральную сумму
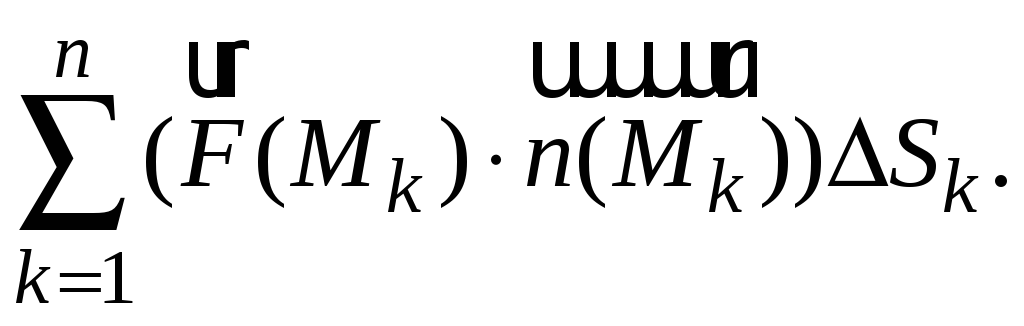 Произведение в круглых скобках –
скалярное произведение двух векторов.
Конечный предел этой интегральной
суммы при
Произведение в круглых скобках –
скалярное произведение двух векторов.
Конечный предел этой интегральной
суммы при
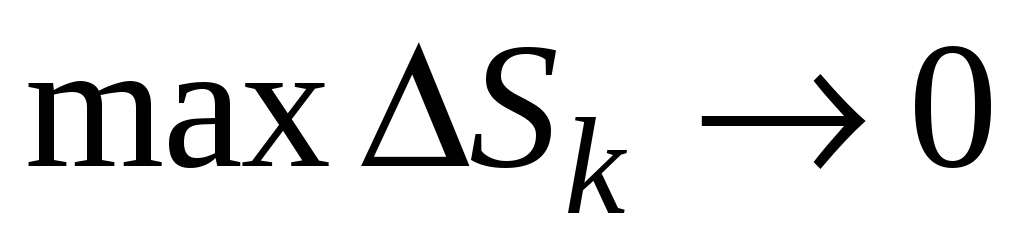 ,
если он не зависит от разбиения
поверхности и от выбора точек
,
если он не зависит от разбиения
поверхности и от выбора точек
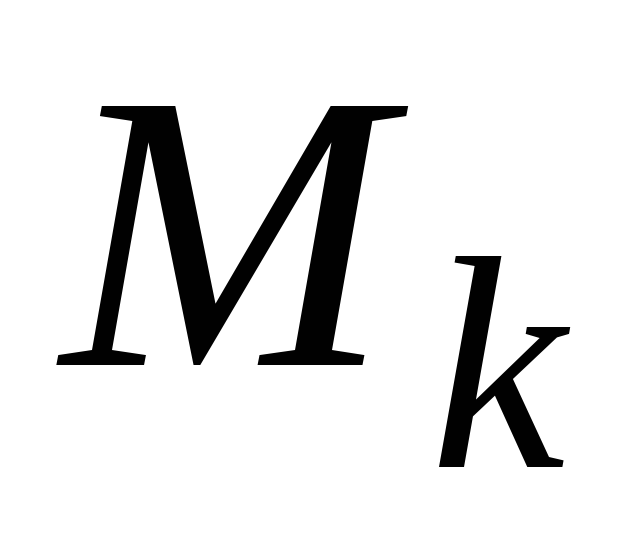 называется поверхностным интегралом
от скалярного поля
называется поверхностным интегралом
от скалярного поля
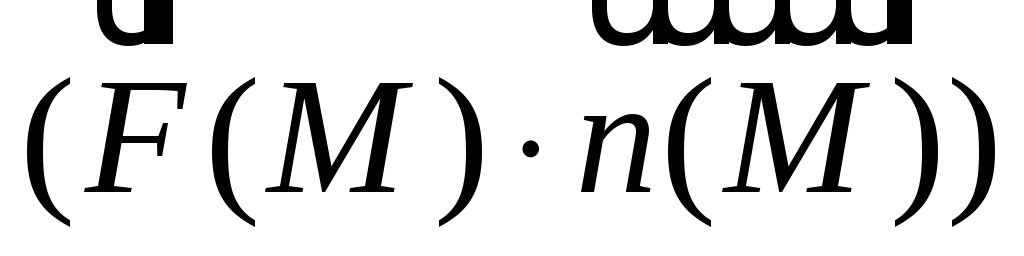 по
поверхности
по
поверхности
 :
:
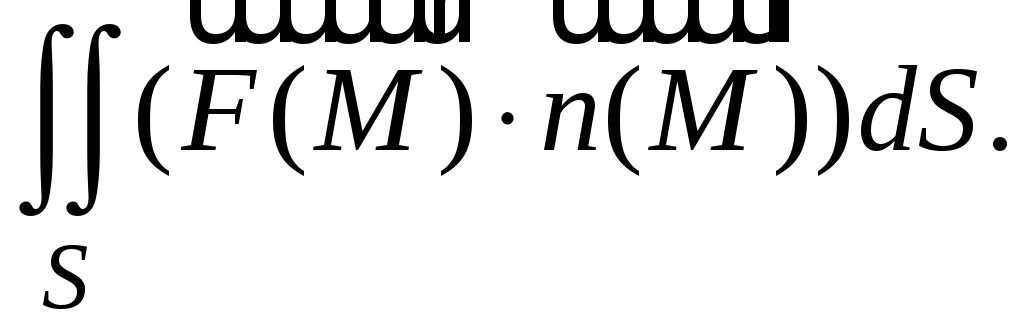 Введем в рассмотрение вектор
Введем в рассмотрение вектор
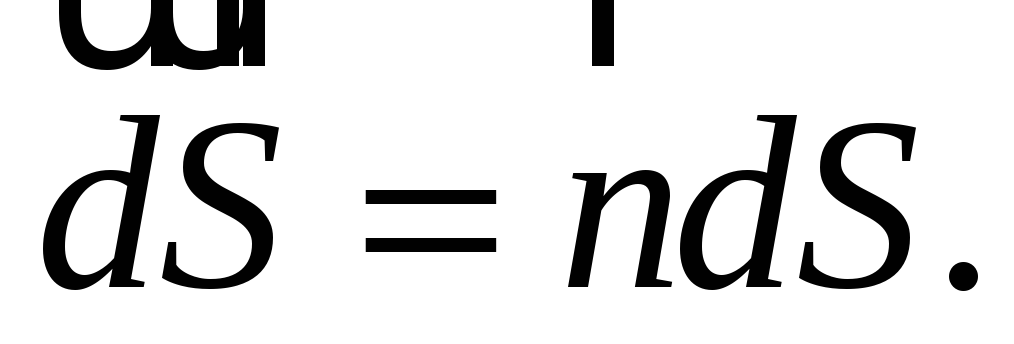 Теперь поверхностный интеграл первого
рода от скалярного поля
Теперь поверхностный интеграл первого
рода от скалярного поля
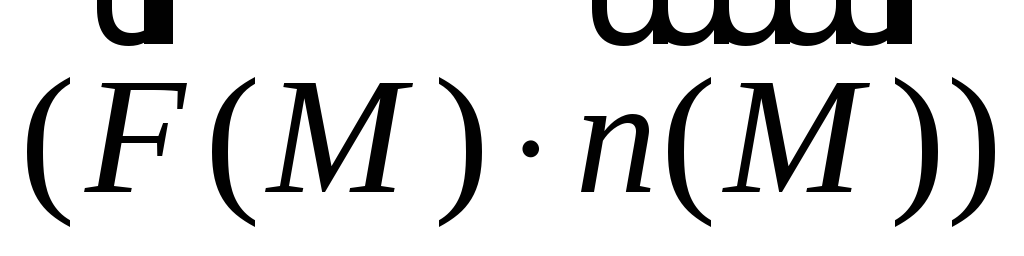 можно переписать в виде поверхностного
интеграла второго рода от векторного
поля
можно переписать в виде поверхностного
интеграла второго рода от векторного
поля
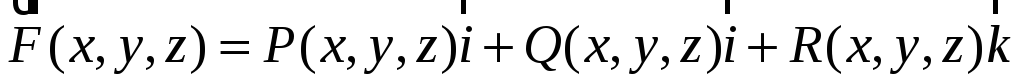 :
:
![]()
-
Для вычисления поверхностного интеграла второго рода сведем его к трем двойным. Для этого раскроем скалярное произведение под знаком интеграла, перемножив соответствующие координаты векторов и сложив произведения. В результате получим:
![]()
![]()
-
Двойные интегралы берутся по проекциям поверхности
 на координатные плоскости.
на координатные плоскости. -
Физический смысл двойного интеграла – поток векторного поля
 через ориентированную поверхность
через ориентированную поверхность
 .
. -
Если в объемно-односвязной области
 задано векторное поле
задано векторное поле
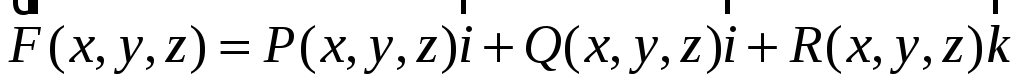 ,
непрерывное вместе с частными производными
,
непрерывное вместе с частными производными
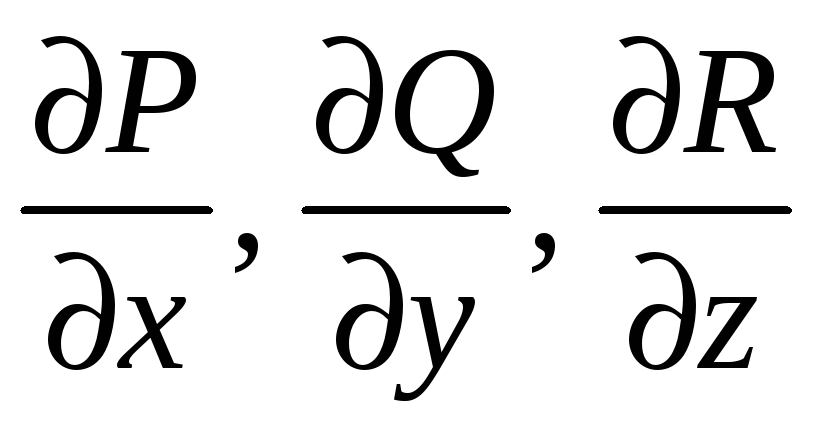 ,
тогда справедлива формула Остроградского
- Гаусса:
,
тогда справедлива формула Остроградского
- Гаусса: -
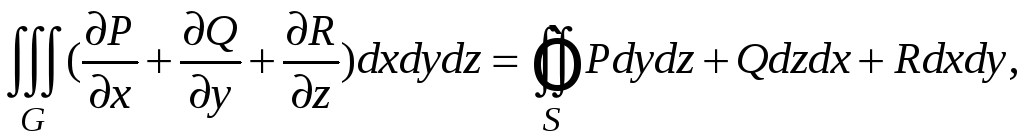
где
поверхностный интеграл берется по
внешней стороне замкнутой поверхности
![]() ,
которая является границей области
,
которая является границей области
![]() .
.
-
Область
 называется объемно-односвязной, если
любая замкнутая поверхность в ней
ограничивает область, целиком лежащую
в
называется объемно-односвязной, если
любая замкнутая поверхность в ней
ограничивает область, целиком лежащую
в
 .
.
Если
функции
![]() таковы, что
таковы, что
![]() ,
то интеграл в левой части равенства
равен объему области
,
то интеграл в левой части равенства
равен объему области
![]() ,
то есть
,
то есть
![]() ,
и мы получаем формулу для вычисления
объема области
,
и мы получаем формулу для вычисления
объема области
![]() с помощью интеграла по ее поверхности
с помощью интеграла по ее поверхности
![]() .
.
Согласно
формальному определению, дивергенция
векторного поля
![]() задается выражением
задается выражением
![]() то есть тройной интеграл в формуле
Остроградского – Гаусса берется от
дивергенции векторного поля.
то есть тройной интеграл в формуле
Остроградского – Гаусса берется от
дивергенции векторного поля.
-
Теперь формулу Остроградского-Гаусса можно записать в векторной форме
-
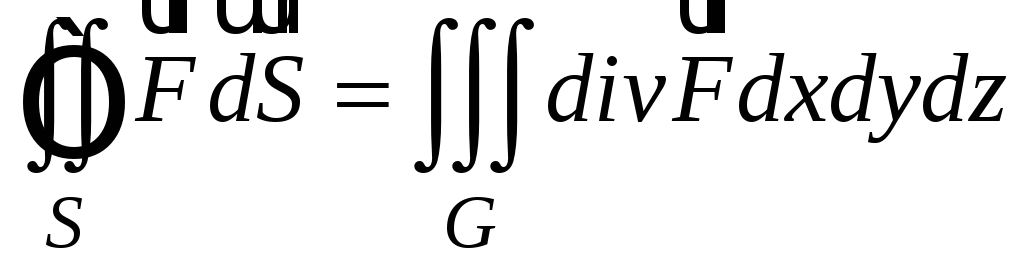
и прочитать следующим образом: поток векторного поля через замкнутую поверхность равен тройному интегралу от дивергенции векторного поля по объему, ограниченному этой поверхностью.
Используя
формулу Остроградского – Гаусса, дадим
физическое определение дивергенции.
Дивергенцией векторного поля
![]() точке
точке
![]() называется плотность его потока в этой
точке, то есть
называется плотность его потока в этой
точке, то есть
Если
в поверхностно односвязной области
![]() задано векторное поле
задано векторное поле
![]() ,
непрерывное вместе с частными производными
,
непрерывное вместе с частными производными
![]() ,
тогда справедлива формула Стокса
,
тогда справедлива формула Стокса
![]()
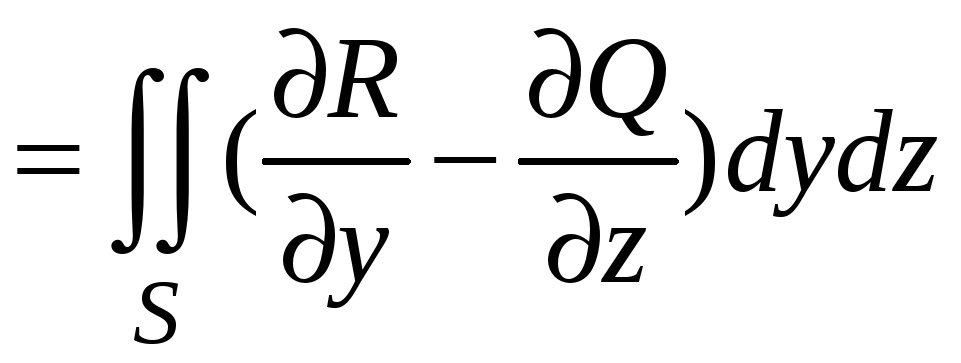
![]()
![]()
где
поверхностный интеграл берется по
внешней стороне поверхности
![]() ,
которая натянута на замкнутый контур
,
которая натянута на замкнутый контур
![]() .
При этом ориентация контура
.
При этом ориентация контура
![]() согласована с ориентацией поверхности
согласована с ориентацией поверхности
![]() ,
то есть при обходе контура сторона
поверхности, по которой берется интеграл,
остается слева.
,
то есть при обходе контура сторона
поверхности, по которой берется интеграл,
остается слева.
-
Трехмерная область называется поверхностно-односвязной, если на любую замкнутую кривую
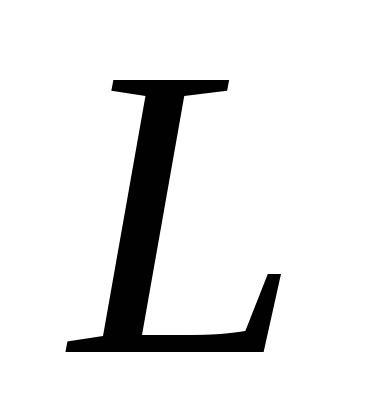 ,
принадлежащую W,
можно натянуть поверхность S,
также полностью принадлежащую W.
,
принадлежащую W,
можно натянуть поверхность S,
также полностью принадлежащую W.
Согласно
формальному определению ротор векторного
поля
![]() задается выражением:
задается выражением:
![]()
![]()
![]()
![]() то есть поверхностный интеграл второго
рода в формуле Стокса берется от ротора
векторного поля.
то есть поверхностный интеграл второго
рода в формуле Стокса берется от ротора
векторного поля.
-
Теперь формулу Стокса можно записать в векторном виде
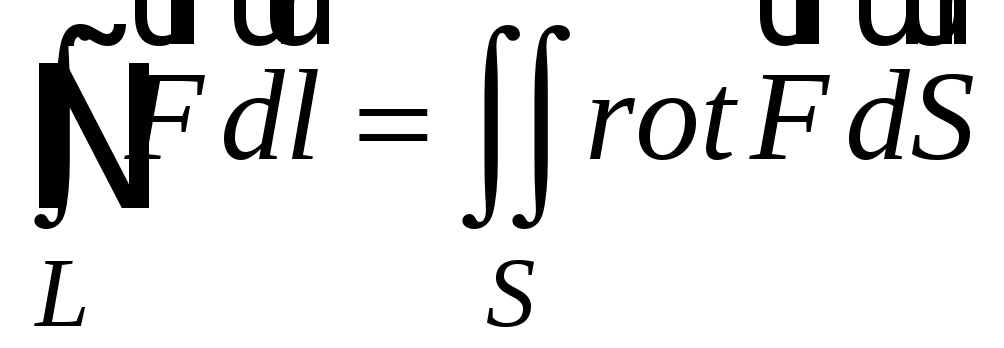 и прочитать следующим образом: циркуляция
векторного поля по замкнутому контуру
равна потоку ротора этого поля через
поверхность, натянутую на данный контур.
и прочитать следующим образом: циркуляция
векторного поля по замкнутому контуру
равна потоку ротора этого поля через
поверхность, натянутую на данный контур. -
Используя формулу Стокса, дадим физическое определение ротора.
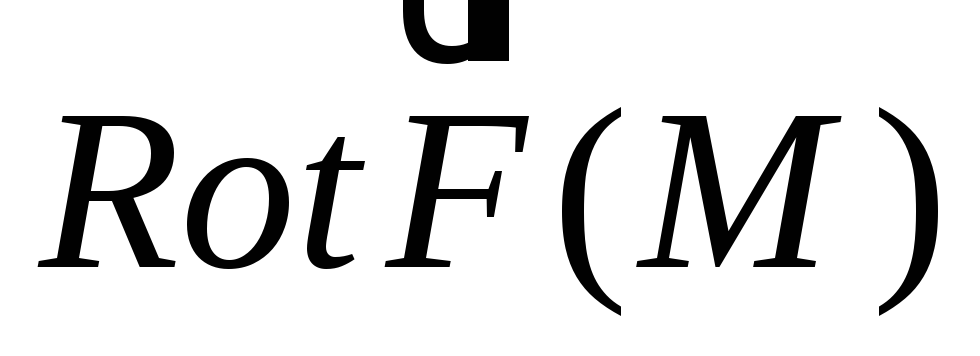 –
вектор, проекция которого на направление
–
вектор, проекция которого на направление
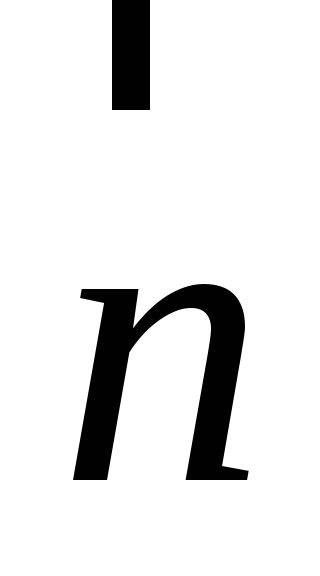 равна пределу отношения циркуляции
поля
равна пределу отношения циркуляции
поля
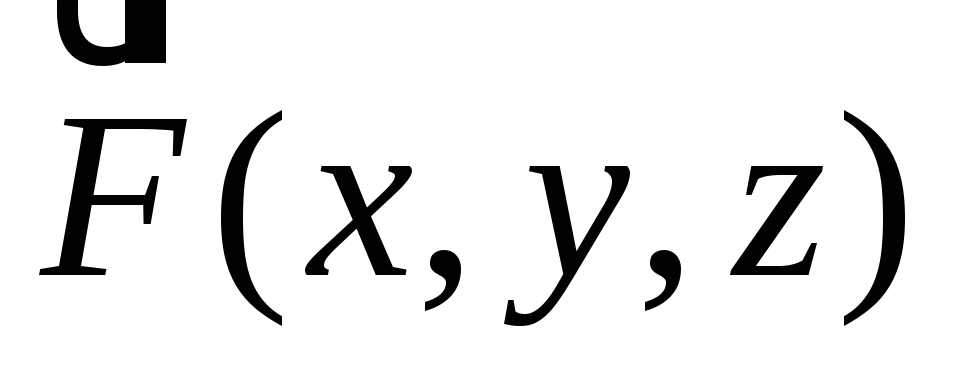 по
плоскому контуру, перпендикулярному
по
плоскому контуру, перпендикулярному
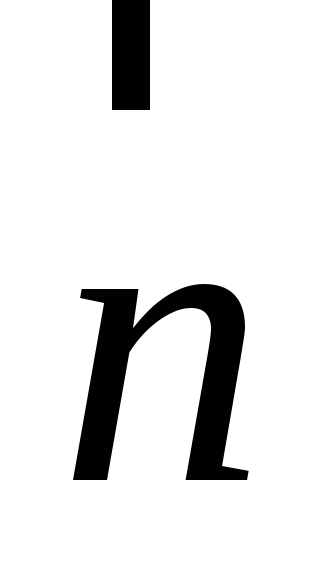 ,
к площади, ограниченной этим контуром,
при стягивании его к точке
,
к площади, ограниченной этим контуром,
при стягивании его к точке
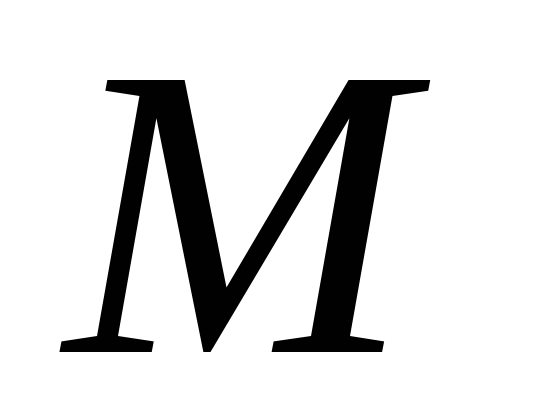 .
.