
- •Модуль 6
- •Задачи для самостоятельного решения
- •Занятие 2
- •Задачи для самостоятельного решения
- •Занятие 3 Поверхностный интеграл первого рода
- •Задачи для самостоятельного решения
- •Занятие 4 Поверхностный интеграл второго рода
- •Задачи для самостоятельного решения
- •Занятие 5 Формула Остроградского – Гаусса. Дивергенция
- •Задачи для самостоятельного решения
- •Формула Стокса. Ротор
- •Задачи для самостоятельного решения
- •Занятие 6 Потенциальное поле (безвихревое поле)
- •Задачи для самостоятельного решения
- •Соленоидальное поле
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
1.
Вычислить поток векторного поля
![]()
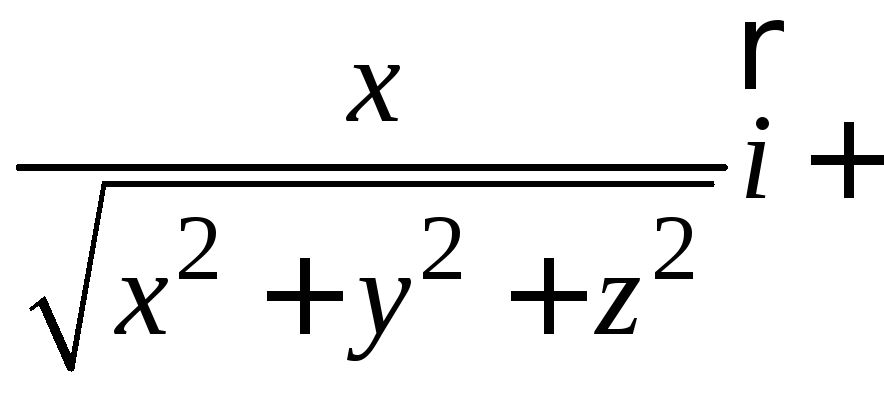

 через поверхность сферы
через поверхность сферы![]() ,
в направлении внешней нормали.
,
в направлении внешней нормали.
2.
Вычислить поток векторного поля
![]()
![]()
![]()
![]() через поверхность куба
через поверхность куба![]() ,
,![]() ,
,![]() ,
в направлении внешней нормали.
,
в направлении внешней нормали.
3.
Вычислить поток векторного поля
![]()
![]() через поверхность тела объемом
через поверхность тела объемом![]() ,
в направлении внешней нормали.
,
в направлении внешней нормали.
Ответы
1. ![]() . 2.
. 2. ![]() .3.
.3. ![]() .
.
Формула Стокса. Ротор
Пример.
Найти
циркуляцию векторного поля
![]() по сечению сферы
по сечению сферы![]() плоскостью
плоскостью![]() .
.
Решение.
Контуром для вычисления циркуляции
является окружность, заданная пересечением
двух поверхностей. Получить ее уравнение
в параметрическом виде достаточно
сложно, поэтому для вычисления циркуляции
воспользуемся формулой Стокса
![]() ,
то есть вместо криволинейного интеграла
по окружности
,
то есть вместо криволинейного интеграла
по окружности![]() мы
будем вычислять поверхностный интеграл
от ротора нашего поля по плоской
поверхности
мы
будем вычислять поверхностный интеграл
от ротора нашего поля по плоской
поверхности![]() ,
натянутой на окружность. Найдем ротор
нашего поля
,
натянутой на окружность. Найдем ротор
нашего поля
 .
.
Вектор
нормали
 .
.
![]()
 .
.
Значение
подынтегральной функции
![]() на поверхности
на поверхности![]() равно
равно![]() ,
поэтому последний интеграл приобретает
вид
,
поэтому последний интеграл приобретает
вид .
Для окончательного вычисления интеграла
необходимо найти площадь круга
.
Для окончательного вычисления интеграла
необходимо найти площадь круга![]() .
Найдем
.
Найдем![]() -
радиус этого круга. Плоскость
-
радиус этого круга. Плоскость![]() пересекает координатные оси в точках
с координатой
пересекает координатные оси в точках
с координатой![]() ,
это значит, что в наш круг вписан
равносторонний треугольник со стороной
,
это значит, что в наш круг вписан
равносторонний треугольник со стороной![]() .
Стороны треугольника лежат на координатных
плоскостях. Радиус круга
.
Стороны треугольника лежат на координатных
плоскостях. Радиус круга![]() будет равен
будет равен![]() ,
а его площадь
,
а его площадь![]() ,
то есть
,
то есть .
Значение искомого потока будет
определяться выражением
.
Значение искомого потока будет
определяться выражением![]() .
Тогда окончательно имеем
.
Тогда окончательно имеем
![]()
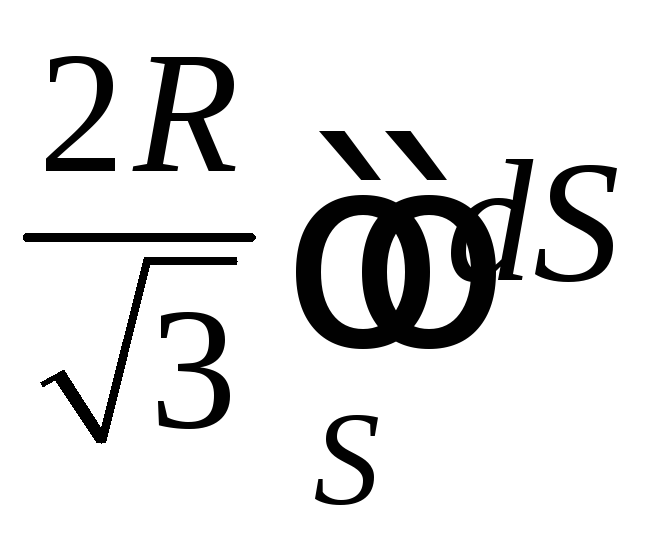
![]() .
.
Пример.
Найти
циркуляцию векторного поля
![]() по контуру, вырезанному из параболоида
по контуру, вырезанному из параболоида![]() плоскостями
плоскостями![]() ,
в положительном направлении относительно
внешней нормали параболоида.
,
в положительном направлении относительно
внешней нормали параболоида.
Решение.
Воспользуемся формулой Стокса и вместо
циркуляции вычислим поток
![]() через поверхность
через поверхность![]() ,
которая вырезается указанными плоскостями
из параболической поверхности. Найдем
ротор:
,
которая вырезается указанными плоскостями
из параболической поверхности. Найдем
ротор:
 .
.
Поверхностный
интеграл от
![]() по параболической поверхности сводим
к трем двойным интегралам по плоским
областям
по параболической поверхности сводим
к трем двойным интегралам по плоским
областям![]() ,
,![]() ,
,![]() -
проекциям параболической поверхности
на координатные плоскости.
-
проекциям параболической поверхности
на координатные плоскости.

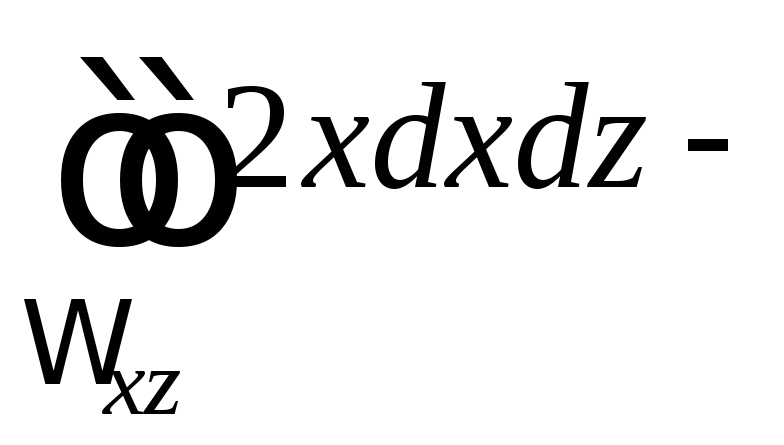
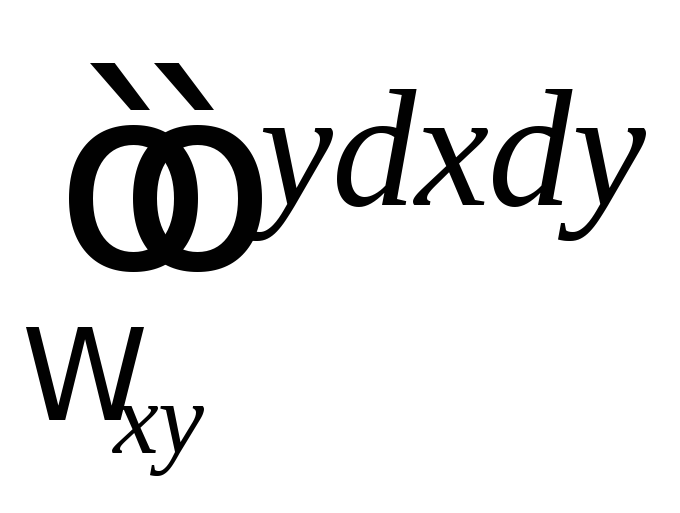 .
.
Два
первых двойных интеграла совпадают с
точностью до обозначений, поэтому они
взаимно уничтожаются. Третий двойной
интеграл по четвертушке круга
![]() вычисляем при помощи замены переменных
вычисляем при помощи замены переменных![]() .
.

 .
.
Пример.
Найти
работу векторного поля
![]() вдоль винтовой линии
вдоль винтовой линии![]() от точки
от точки![]() до точки
до точки![]() .
.
Решение. Заметим, что ротор нашего поля равен нулю.
 .
.
Дополним
винтовую линию
![]() отрезком
отрезком![]() до замкнутого контура
до замкнутого контура![]() .
Тогда, согласно формуле Стокса, имеем:
.
Тогда, согласно формуле Стокса, имеем:
![]()
![]() .
.
Отсюда
![]()
![]() .
Таким образом, для того чтобы найти
работу нашего векторного поля по винтовой
линии
.
Таким образом, для того чтобы найти
работу нашего векторного поля по винтовой
линии![]() необходимо вычислить интеграл от этого
поля по отрезку
необходимо вычислить интеграл от этого
поля по отрезку![]() .
Так как на отрезке
.
Так как на отрезке![]()
![]() и
и![]() имеем:
имеем:
![]()
 .
.
Пример.
Вывести теорему о циркуляции
![]() - циркуляция индукции магнитного поля
вдоль замкнутого контура
- циркуляция индукции магнитного поля
вдоль замкнутого контура![]() равна току, охватываемому этим контуром,
умноженному на магнитную постоянную
вакуума.
равна току, охватываемому этим контуром,
умноженному на магнитную постоянную
вакуума.
Решение.
Рассмотрим индукцию магнитного поля,
созданного электрическим током
![]() ,
протекающим по проводу, расположенному
вдоль оси
,
протекающим по проводу, расположенному
вдоль оси![]() ,
, .
Ротор и дивергенция этого поля во всех
точках пространства кроме точек, лежащих
на оси
.
Ротор и дивергенция этого поля во всех
точках пространства кроме точек, лежащих
на оси![]() ,
равны нулю. Циркуляцию поля
,
равны нулю. Циркуляцию поля![]() по окружности
по окружности![]() ,
охватывающей ось
,
охватывающей ось![]() ,
невозможно вычислить при помощи формулы
С
,
невозможно вычислить при помощи формулы
С токса.
Поле не определено на оси
токса.
Поле не определено на оси![]() и пространство не является
поверхностно-односвязным, поэтому
формула Стокса не справедлива. Циркуляцию
поля
и пространство не является
поверхностно-односвязным, поэтому
формула Стокса не справедлива. Циркуляцию
поля![]() по окружности
по окружности![]() вычислим
непосредственно через криволинейный
интеграл второго рода
вычислим
непосредственно через криволинейный
интеграл второго рода![]() .
В каждой точке окружности
.
В каждой точке окружности![]() поле
поле![]() направлено по касательной к кривой и
его модуль равен
направлено по касательной к кривой и
его модуль равен![]() ,
поэтому
,
поэтому![]()
 .
Мы воспользовались тем, что
.
Мы воспользовались тем, что![]() равен длине нашей окружности
равен длине нашей окружности![]() .
Покажем, что результат не изменится,
если ток будет протекать не через центр
круга. Для этого сместим окружность
перпендикулярно оси
.
Покажем, что результат не изменится,
если ток будет протекать не через центр
круга. Для этого сместим окружность
перпендикулярно оси![]() на расстояние, не превосходящее
на расстояние, не превосходящее![]() .
Применим формулу Стокса для контура,
охватывающего поверхность
.
Применим формулу Стокса для контура,
охватывающего поверхность![]() ,
,
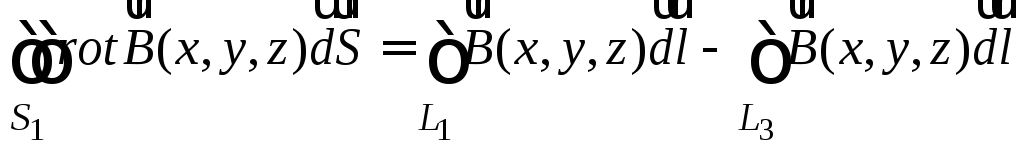 .
.
Поверхностный
интеграл в левой части формулы равен
нулю, так как
![]() равен нулю во всех точках кроме точек,
принадлежащих оси
равен нулю во всех точках кроме точек,
принадлежащих оси![]() .
Отсюда следует, что
.
Отсюда следует, что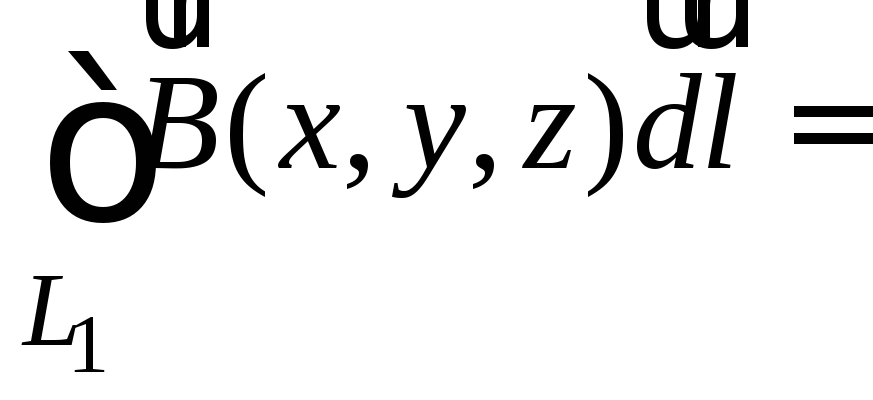
 .
Аналогично показываем, что
.
Аналогично показываем, что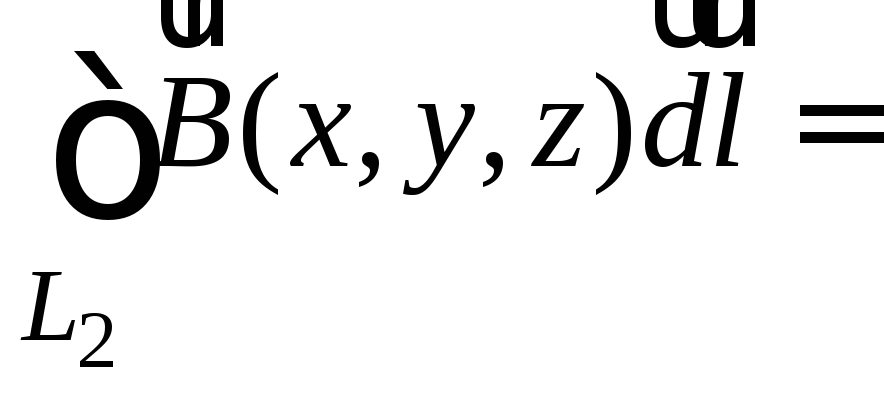
 .
Так как циркуляция поля
.
Так как циркуляция поля![]() по окружности
по окружности![]() равна
равна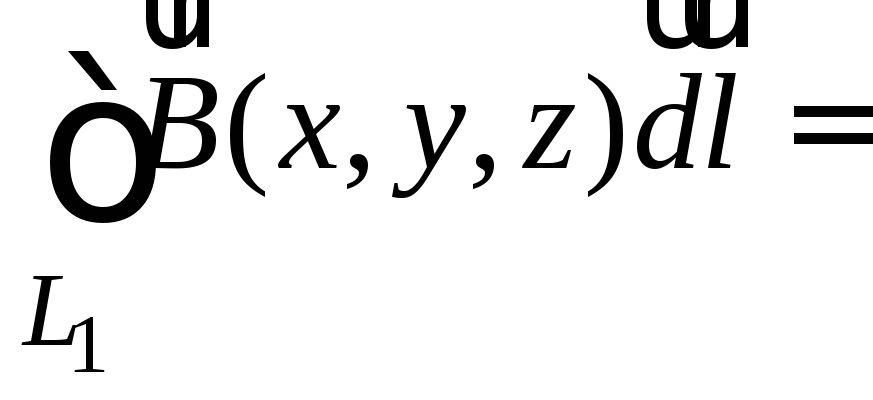
 ,
а циркуляция поля по смещенной окружности
равна
,
а циркуляция поля по смещенной окружности
равна
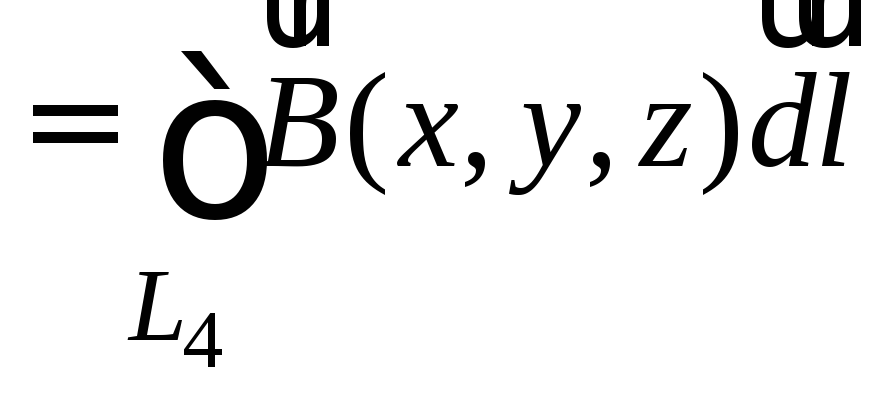 ,
то они одинаковые и равны
,
то они одинаковые и равны![]() .
Таким образом, циркуляция поля
.
Таким образом, циркуляция поля![]() по окружности
по окружности![]() равна
равна![]() ,
где
,
где![]() -
любой ток, охватываемый окружностью.
Деформируя окружность произвольным
образом добавлением и вычитанием
поверхностей
-
любой ток, охватываемый окружностью.
Деформируя окружность произвольным
образом добавлением и вычитанием
поверхностей![]() ,
,![]() и т.д., распространим этот результат на
любой замкнутый контур. Используя
аддитивность токов и созданных ими
полей, распространяем результат на
любое количество токов, охватываемых
контуром, и получаем теорему Гаусса -
циркуляция индукции магнитного поля
вдоль замкнутого контура
и т.д., распространим этот результат на
любой замкнутый контур. Используя
аддитивность токов и созданных ими
полей, распространяем результат на
любое количество токов, охватываемых
контуром, и получаем теорему Гаусса -
циркуляция индукции магнитного поля
вдоль замкнутого контура![]() равна току, охватываемому этим контуром,
умноженному на магнитную постоянную
вакуума.
равна току, охватываемому этим контуром,
умноженному на магнитную постоянную
вакуума.
