Задачи для самостоятельного решения

1. Вычислить циркуляцию поля по кругув положительном направлении.

2. Вычислить поток векторного поля через часть сферыв направлении внешней нормали.

Ответы

1.  . 2.  .

Занятие 6 Потенциальное поле (безвихревое поле)

Пример. Найти потенциал векторного поля

Решение. Так как данное поле определено во всем пространстве, то есть в поверхностно-односвязной области, для его потенциальности достаточно, чтобы ротор был равен нулю. Проверим это.

Для нахождения потенциала вычислим криволинейный интеграл от точкис координатамидо точкис координатами. Криволинейный интеграл от потенциального поля не зависит от формы пути, поэтому интегрирование будем проводить по ломаной прямой, расположенной между точками:,,,.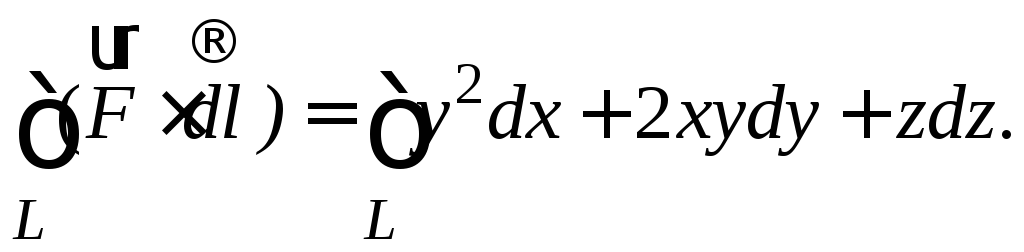При интегрировании по первому отрезку ломаной, лежащему на оси, все три интеграла обращаются в ноль. Первый из-за равенства нулю функции, а два других из-за равенства нулюи. При интегрировании по второму отрезку ломаной, лежащему в плоскостипараллельно оси, первый и третий интегралы равны нулю, так как. Вычисляя второй, получаемИнтегрирование по третьему отрезку, параллельному осидаетТаким образом, если значение потенциала в начале координат принять за ноль, искомый потенциал в произвольной точке с координатамибудет равен

Пример. Показать, что электростатическое поле положительного точечного заряда

потенциально и найти его потенциал.

Решение. Электростатическое поле положительного точечного заряда определено во всех точках кроме одной точки начала координат, то есть в поверхностно односвязной области. Во всех точках существования, как мы уже показывали, ротор поля равен нулю, а, значит, наше поле потенциально. Для электростатического поля за ноль удобно брать потенциал бесконечно удаленной точки. Чтобы найти потенциал в произвольной точке, необходимо вычислить криволинейный интеграл второго рода нашего поля по кривой от бесконечно удаленной точки до точки, то есть найти работу (с точностью до некоторого множителя) по переносу положительного пробного заряда из бесконечности в заданную точку. Так как поле потенциально, интеграл не зависит от формы пути, а определяется только начальной и конечной точками. Для удобства вычисления интегрирование будем проводить по ломаной прямой,,,. Итак, потенциал определяется интегралом:

.

Интегрируя по первому участку ломаной прямой, на котором получаем

Интегрирование по второму участку, где: дает

Интегрируя по третьему участку ломаной линии, на котором имеем

Складываем результаты интегрирования по трем участкам, умножаем на и получаем:

При перемещении положительного пробного заряда из бесконечности в точку поля положительного точечного заряда внешней силой совершается положительная работа, поэтому обычно считают, что потенциалто есть для его определения используют формулу

Пример. Определить потенциальность индукции магнитного поля, создаваемого электрическим током , протекающим по проводу, расположенному вдоль оси

.

Решение. Как мы уже установили, ротор этого поля равен нулю во всех точках, где поле существует. Оно существует во всех точках пространства кроме точек оси . Так как пространство с выколотыми точками осине является поверхностно односвязной областью (на контур, охватывающий ось, нельзя натянуть поверхность, целиком принадлежащую области), то равенство нулю ротора не является достаточным условием потенциальности нашего поля. Необходимым и достаточным условием потенциальности векторного поля является независимость его работы от формы пути, а также равенство нулю работы по замкнутому контуру. Интегрирование поля по замкнутому контуру, охватывающему ось, дает не нулевой результат (проекция векторана векторположительная вдоль всего контура). Результат интегрирования поляот точкидо точкизависит от того, сколько оборотов делает криваявокруг оси. Таким образом, можно утверждать, что индукция магнитного поляне является потенциальным полем.