
- •Модуль 6
- •Задачи для самостоятельного решения
- •Занятие 2
- •Задачи для самостоятельного решения
- •Занятие 3 Поверхностный интеграл первого рода
- •Задачи для самостоятельного решения
- •Занятие 4 Поверхностный интеграл второго рода
- •Задачи для самостоятельного решения
- •Занятие 5 Формула Остроградского – Гаусса. Дивергенция
- •Задачи для самостоятельного решения
- •Формула Стокса. Ротор
- •Задачи для самостоятельного решения
- •Занятие 6 Потенциальное поле (безвихревое поле)
- •Задачи для самостоятельного решения
- •Соленоидальное поле
- •Задачи для самостоятельного решения
Занятие 3 Поверхностный интеграл первого рода
Пример.
Вычислить площадь параболической
поверхности
![]()
Решение.
Площадь поверхности определяется
поверхностным интегралом первого
рода:![]() .
Спроектируем нашу параболическую
поверхность на плоскость
.
Спроектируем нашу параболическую
поверхность на плоскость![]() ,
то есть на круг с радиусом
,
то есть на круг с радиусом![]() ,
и, учитывая, что
,
и, учитывая, что![]() ,
заменим поверхностный интеграл
соответствующим двойным:
,
заменим поверхностный интеграл
соответствующим двойным: .
Переходя к полярной системе координат
и сводя двойной интеграл к повторному
интегралу, окончательно получаем:
.
Переходя к полярной системе координат
и сводя двойной интеграл к повторному
интегралу, окончательно получаем:

Пример.
Вычислить массу параболической
поверхности
![]() ,
плотность которой меняется по закону
,
плотность которой меняется по закону![]()
Решение.
Масса поверхности определяется интегралом
![]() На нашей поверхности выполняется
равенство
На нашей поверхности выполняется
равенство![]() и она проектируется на плоскость
и она проектируется на плоскость![]() в круг с радиусом
в круг с радиусом![]() .
Учитывая, что
.
Учитывая, что![]() ,
заменим поверхностный интеграл
соответствующим двойным:
,
заменим поверхностный интеграл
соответствующим двойным: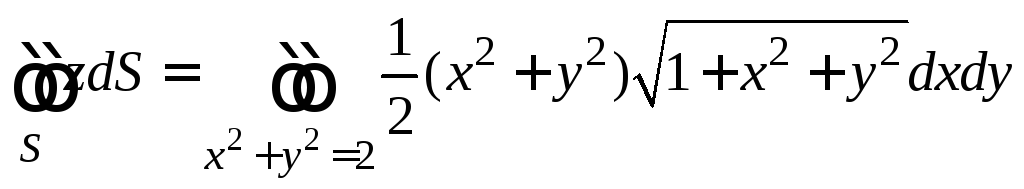 .
Перейдем к полярным координатам и в
результате найдем:
.
Перейдем к полярным координатам и в
результате найдем:
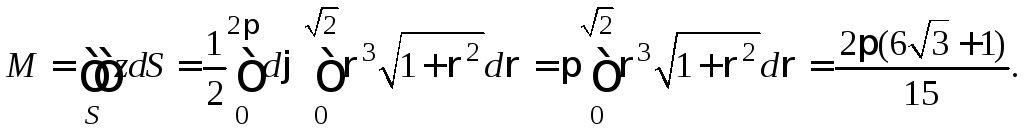
Последний
интеграл вычислялся при помощи замены
![]()
Пример.
Вычислить поверхностный интеграл:
![]() где
где![]() -
часть конической поверхности
-
часть конической поверхности![]() вырезанная цилиндрической поверхностью
вырезанная цилиндрической поверхностью![]()
Решение.
Поверхность, по которой мы производим
интегрирование, проектируется на
плоскость
![]() в круг
в круг![]() ,
при этом элемент конической поверхности
,
при этом элемент конической поверхности![]() преобразуется
следующим образом
преобразуется
следующим образом![]() ,
поэтому двойной интеграл будет иметь
вид:
,
поэтому двойной интеграл будет иметь
вид:

Перейдем в интеграле к полярным координатам и получим:

Задачи для самостоятельного решения
1.
Найти массу поверхности полусферы
![]() ,
если в каждой ее точке поверхностная
плотность вещества пропорциональна
расстоянию от оси
,
если в каждой ее точке поверхностная
плотность вещества пропорциональна
расстоянию от оси![]() .
.
2.
Найти момент инерции относительно оси
![]() однородной сферической оболочки
однородной сферической оболочки![]() .
.
Ответы
1. ![]() .2.
.2. ![]() .
.
Занятие 4 Поверхностный интеграл второго рода
Пример.
Вычислить поток векторного поля
![]()

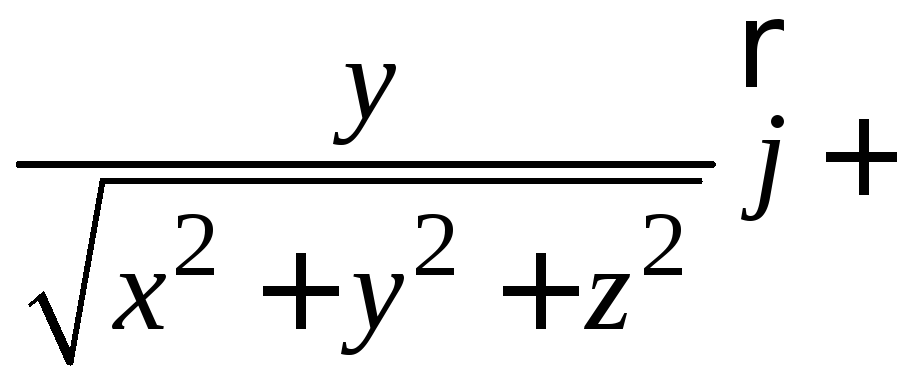
 через поверхность сферы
через поверхность сферы![]() ,
в направлении внешней нормали.
,
в направлении внешней нормали.
Решение.
Поток векторного поля будем вычислять
как поверхностный интеграл первого
рода от скалярного поля
![]() ,
где
,
где![]() -
вектор единичной нормали к нашей
сферической поверхности. Так как наше
поле центрально-симметричное, вектора
-
вектор единичной нормали к нашей
сферической поверхности. Так как наше
поле центрально-симметричное, вектора![]() и
и![]() параллельны. Модуль вектора
параллельны. Модуль вектора![]() везде, кроме начала координат, равен
единице. Поэтому имеем
везде, кроме начала координат, равен
единице. Поэтому имеем
![]()
![]() .
.
Пример.
Вычислить поток векторного поля
![]()
![]()
![]() через внешнюю поверхность сферы
через внешнюю поверхность сферы![]()
Решение. Поверхностный интеграл второго рода будем вычислять сведением его к двойным интегралам по проекциям нашей сферы на координатные плоскости:
![]()
Рассмотрим
третий из них – по
![]() -
проекции
-
проекции![]() на плоскость
на плоскость![]() :
: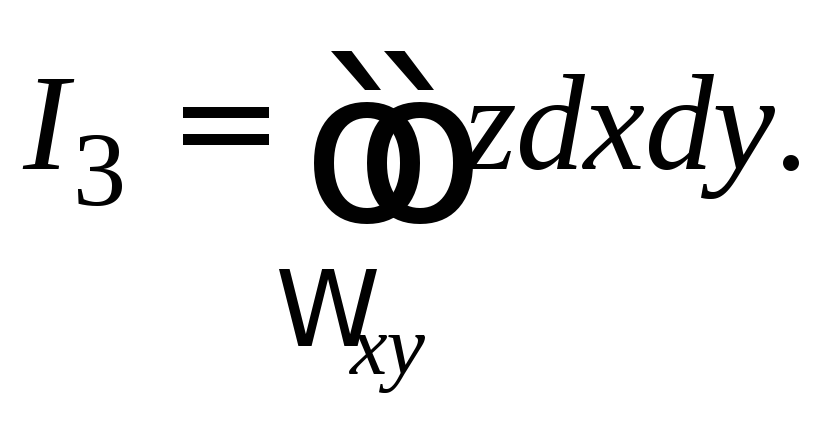 Внешняя нормаль верхней половины сферы,
на которой выполняется равенство
Внешняя нормаль верхней половины сферы,
на которой выполняется равенство![]() ,
образует с осью
,
образует с осью![]() острый угол. На нижней половине сферы
выполняется равенство
острый угол. На нижней половине сферы
выполняется равенство![]() ,
и ее внешняя нормаль образует с осью
,
и ее внешняя нормаль образует с осью![]() тупой угол, поэтому двойной интеграл
по проекции
тупой угол, поэтому двойной интеграл
по проекции![]() будет иметь вид:
будет иметь вид: Так как проекция
Так как проекция![]() является кругом радиуса
является кругом радиуса![]() ,
переходим к полярной системе координат
и в итоге получаем:
,
переходим к полярной системе координат
и в итоге получаем:

Так
как три двойных интеграла по проекциям
нашей сферы на координатные плоскости
одинаковы, окончательным результатом
будет
![]()
Пример.
Вычислить поток векторного поля
![]()
![]()
![]() через внешнюю поверхностьS
конуса
через внешнюю поверхностьS
конуса
![]()
Решение.
Поверхностный интеграл от векторного
поля будем вычислять как поверхностный
интеграл первого рода от скалярного
поля
![]() ,
где
,
где![]() -
вектор единичной нормали к конической
поверхности. Сначала находим вектор
нормали
-
вектор единичной нормали к конической
поверхности. Сначала находим вектор
нормали![]() ,
где
,
где![]() ,
затем нормируем его, разделив на
,
затем нормируем его, разделив на![]() Перемножив скалярно вектора
Перемножив скалярно вектора![]() и
и![]() ,
записываем поверхностный интеграл
первого рода
,
записываем поверхностный интеграл
первого рода .
Проектируем коническую поверхность на
плоскость
.
Проектируем коническую поверхность на
плоскость![]() и переходим к двойному интегралу по
кругу
и переходим к двойному интегралу по
кругу![]() :
:

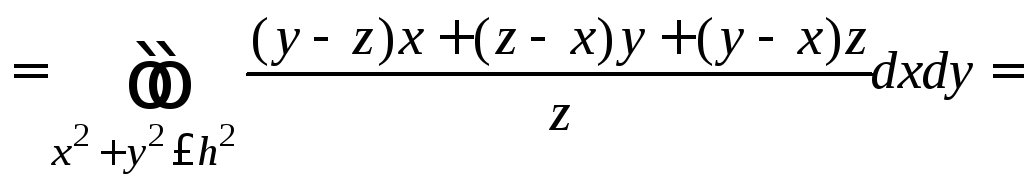

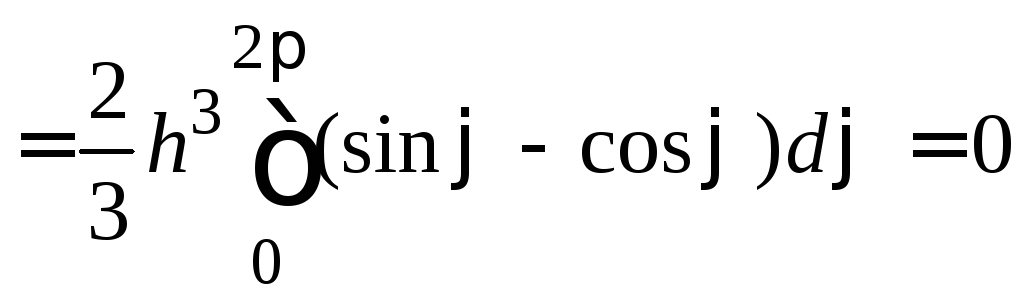 .
.
Пример.
Вычислить поток векторного поля
![]()
![]()
![]() через внешнюю часть сферы
через внешнюю часть сферы![]() ,
расположенную в первом октанте, в
направлении внешней нормали.
,
расположенную в первом октанте, в
направлении внешней нормали.
Решение.
Поверхностный интеграл от векторного
поля будем вычислять как поверхностный
интеграл первого рода от скалярного
поля
![]() ,
где
,
где![]() -
вектор единичной нормали к нашей
сферической поверхности, описываемой
уравнением
-
вектор единичной нормали к нашей
сферической поверхности, описываемой
уравнением![]() .
Сначала находим вектор нормали
.
Сначала находим вектор нормали![]() ,
где
,
где![]() ,
затем нормируем его, разделив на
,
затем нормируем его, разделив на![]() ,
и получим, очевидно,
,
и получим, очевидно,![]()
![]()
![]() .
Перемножив скалярно вектора
.
Перемножив скалярно вектора![]() и
и![]() ,
записываем поверхностный интеграл
первого рода
,
записываем поверхностный интеграл
первого рода![]()
![]() .
Проектируем сферическую поверхность
.
Проектируем сферическую поверхность![]() на плоскость
на плоскость![]() и переходим к двойному интегралу по
четвертушке круга
и переходим к двойному интегралу по
четвертушке круга![]() :
:![]() .
.


 .
.
Найдем
теперь поток нашего векторного поля,
вычислив поверхностный интеграл второго
рода
![]() .
Сведем его к трем двойным интегралам
по проекциям сферической поверхности
.
Сведем его к трем двойным интегралам
по проекциям сферической поверхности![]() на координатные плоскости
на координатные плоскости

 .
Первый и третий интегралы взаимно
уничтожаются, второй при вычислении
дает, очевидно, четвертую часть площади
круга
.
Первый и третий интегралы взаимно
уничтожаются, второй при вычислении
дает, очевидно, четвертую часть площади
круга![]()
