Модуль 6

«Криволинейные, поверхностные интегралы. Элементы теории поля»

дисциплины

«Математический анализ»

Методическое пособие к практическим занятиям

Методическое пособие к практическим занятиям предназначено для оказания помощи студентам по самостоятельному решению вне аудитории заданий, указанных в семестровом плане (см. документ «План практических занятий»). В нем приводятся подробные решения типовых задач. Особое внимание уделяется наиболее сложным (узловым) этапам решений. После разбора решений типовых заданий настоятельно рекомендуется решить предлагаемые задания для самостоятельного решения.

Занятие 1

Криволинейный интеграл первого рода

Пример. Вычислить криволинейный интеграл первого рода вдоль логарифмической кривой при.

Решение. Примем за параметр переменную тогда параметрическое уравнение нашей кривой будет иметь видПо формуле сведения криволинейного интеграла к определенному интегралу имеем:

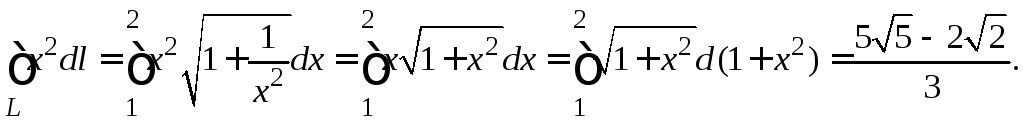
Пример. Найти массу верхней половины окружности если плотность в каждой точке окружности определяется ее ординатой.

Решение. Параметрическое уравнение нашей кривой Массу полуокружности находим при помощи криволинейного интеграла первого рода

Пример. Найти момент инерции однородной окружности , если ось вращения совпадает с осью.

Решение. Момент инерции элемента дугиоднородной окружности равен произведению массы этого элемента, которая равна(плотность дуги принимаем за единицу), на квадрат расстоянияэтого элемента от оси вращения. Производя суммирование по всей окружности, приходим к криволинейному интегралу. Подынтегральная функцияна окружностиравна, поэтому. При вычислении последнего интеграла мы воспользовались тем, чторавен длине окружности.

Пример. Найти момент инерции однородной окружности относительно ее диаметра.

Решение. Момент инерции элемента дугиоднородной окружности равен произведению массы этого элемента, которая равна(плотность дуги принимаем за единицу), на квадрат расстоянияэтого элемента от диаметра, совпадающего с осью. Производя суммирование по всей окружности, приходим к криволинейному интегралу. Запишем уравнение окружности в параметрическом виде. Перейдем от криволинейного интеграла первого рода к определенному интегралу, учитывая, что,. 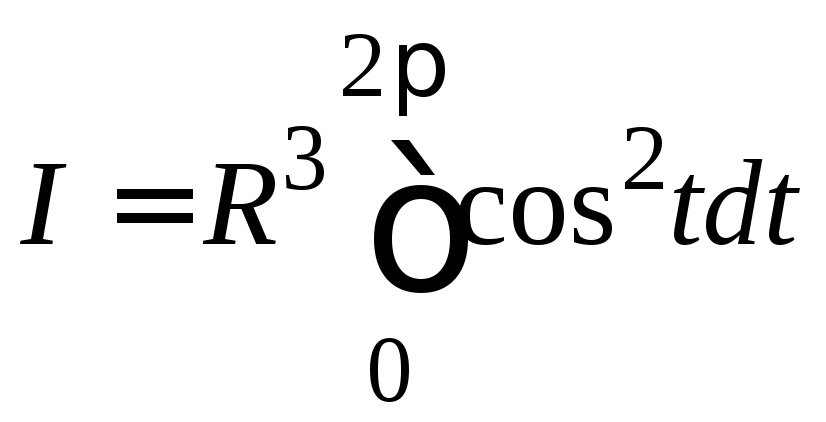Используя результат предыдущего примера, можно на примере окружности убедиться в справедливости теоремы механики, которая утверждает, что моменты инерции плоского тела, лежащего в плоскости, удовлетворяют равенству.

Пример. Вычислить криволинейный интеграл 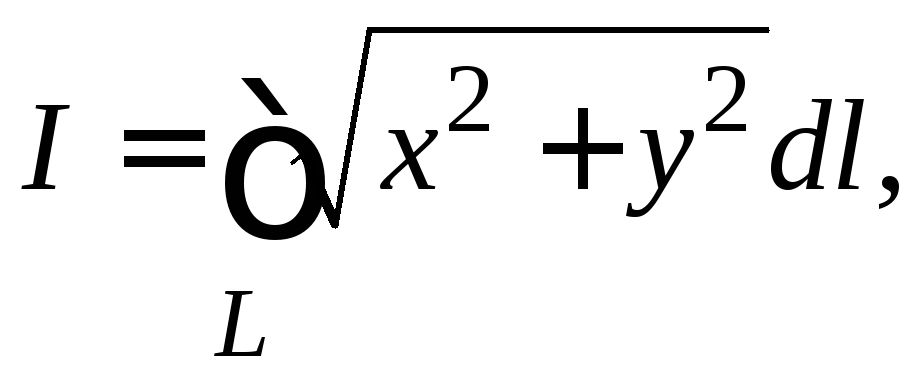где- окружность.

Решение. Перейдем к полярным координатам: Уравнение нашей окружности будет иметь видПолярный уголвозьмем в качестве параметраи запишем уравнение окружности в виде:Тогда на этой окружности подынтегральная функцияпринимает значение, а элементарная дугавыражается формулой. Переходим к определенному интегралу и окончательно получаем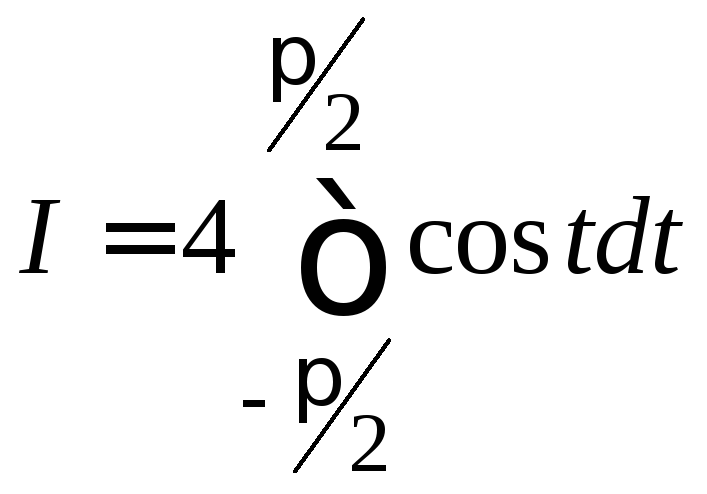

Пример. Вычислить интеграл где- линия пересечения сферыи плоскости.

Решение. Плоскость проходит через начало координат и пересекает сферупо окружности радиуса. Из соображений симметрии, откуда следует равенство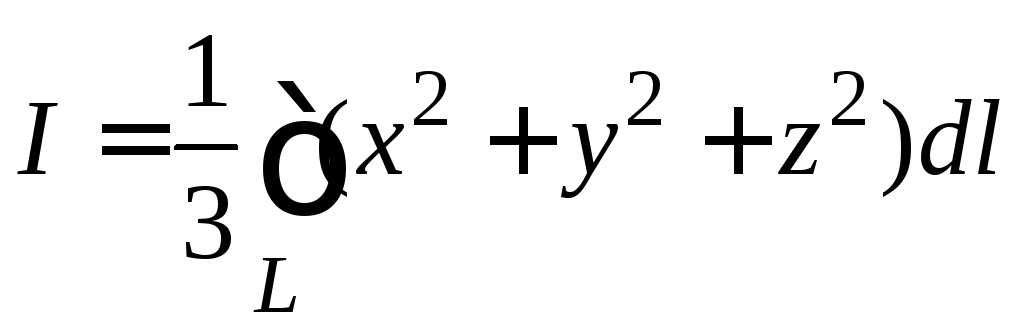. Подынтегральная функция на кривойпринимает значение, равное, так как криваялежит на сфере. Наш интеграл принимает вид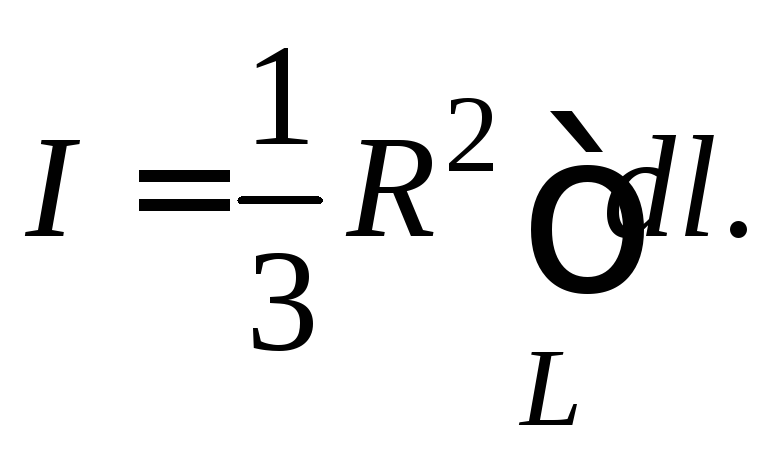Интегралравен длине окружности, следовательно,