Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Калининградский государственный технический университет»

Кафедра систем управления и вычислительной техники

Топоркова О.М.

Методические указания

для выполнения самостоятельных работ

ПО ДИСЦИПЛИНЕ «ИНФОРМАТИКА»

Калининград 2011

Оглавление

1. Перевод чисел из одной системы счисления в другую 3

2. Построение прямых кодов и кодирование дискретного сигнала 8

3. Построение кодов с учетом частоты символов и кодирование дискретного сигнала 9

4. Построение кода Грея и кодирование дискретного сигнала 10

5. Криптографическое кодирование дискретного сигнала методом простой подстановки 11

6. Криптографическое кодирование дискретного сигнала методом Виженера 12

7. Построение эффективных кодов методом Шеннона-Фано и кодирование дискретного сигнала 13

8. Построение эффективных кодов методом Хаффмена и кодирование дискретного сигнала 14

9. Измерение дискретного сигнала 16

10. Сложение вещественных чисел в обратных кодах 17

11. Сложение вещественных чисел в дополнительных кодах 19

1. Перевод чисел из одной системы счисления в другую

Задание к работе: выполнить перевод вещественного числа по схеме:

двоичная шестнадцатеричная

система система

исходное десятичная

число система

шестнадцатеричная двоичная

система система

При этом:

1. вещественное число получить из номера своей зачетной книжки по следующему правилу: старшие 3 цифры сделать целой частью числа, оставшиеся цифры – дробной частью числа. Например, если номер зачетной книжки 12345, то вещественное число имеет значение 123,45;

2. перевод в двоичную систему выполнять до 9 знаков точности, в шестнадцатеричную – до 3 знаков.

Решение задачи

Правила перевода различаются в зависимости от формата числа – целое или правильная дробь. Для вещественных чисел используется комбинация правил перевода для целого числа и правильной дроби.

1.1. Правила перевода целых чисел

Результатом перевода всегда является целое число. Рассмотрим следующие группы правил:

• из десятичной системы – в двоичную и шестнадцатеричную,

• из двоичной и шестнадцатеричной системы – в десятичную,

• из двоичной системы в шестнадцатеричную и обратно.

1.1.1. Перевод из десятичной системы счисления – в двоичную и шестнадцатеричную:

а) число делится на основание системы счисления, в которую переводится (2 или 16); получается частное и остаток;

б) если полученное частное меньше основания системы счисления, в которую выполняется перевод, процесс деления прекращается, переходят к шагу в). Иначе над частным выполняют действия, описанные в шаге а);

в) все полученные остатки и последнее частное преобразуются в соответствии с таблицей 3.1 в цифры той системы счисления, в которую выполняется перевод:

Таблица 3.1

Десятичная система	Двоичная система	Шестнадцатеричная система
0	0	0
1	1	1
2	10	2
3	11	3
4	100	4
5	101	5
6	110	6
7	111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F
16	10000	10

г) формируется результирующее число: его старший разряд – последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым. Таким образом, младший разряд полученного числа – первый остаток от деления, а старший – последнее частное.

Пример 1.1. Выполнить перевод числа 19 в двоичную систему счисления:

_19 2

18. _9 2

1 8 _4 2

1 4 _2 2

0 2 1

0 последнее частное от деления (1<2). Это старший разряд результирующего двоичного числа.

1 0 0 1 1 – результирующее число.

Таким образом, 19 = 10011₂.

Пример 1.2. Выполнить перевод числа 19 в шестнадцатеричную систему счисления:

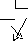_19 16

16 1

3

1. 3 – результирующее число.

Таким образом, 19 = 13₁₆.

Пример 1.3. Выполнить перевод числа 123 в шестнадцатеричную систему счисления:

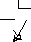_123 16

112 7

11

7 В – результирующее число.

Таким образом, 123 = 7В₁₆.

1.1.2. Перевода из двоичной и шестнадцатеричной систем счисления – в десятичную. В этом случае рассчитывается полное значение числа.

Пример 1.4. Выполнить перевод числа 13₁₆ в десятичную систему счисления. Имеем:

13₁₆ = 1*16¹ + 3*16⁰ = 16 + 3 = 19.

Таким образом, 13₁₆ = 19.

Пример 1.5. Выполнить перевод числа 10011₂ в десятичную систему счисления. Имеем:

10011₂ = 1*2⁴ + 0*2³ + 0*2² + 1*2¹ + 1*2⁰ = 16+0+0+2+1 = 19.

Таким образом, 10011₂ = 19.

1.1.3. Перевод из двоичной системы счисления в шестнадцатеричную:

а) исходное число разбивается на тетрады (т.е. 4 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4;

б) каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с таблицей 3.2:

Таблица 3.2

Двоичная система	Шестнадцатеричная система
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Пример 1.6. Выполнить перевод числа 10011₂ в шестнадцатеричную систему счисления.

Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4 числа цифр. Имеем:

10011₂ = 00010011₂

первая тетрада – младшая цифра числа

вторая тетрада – старшая цифра числа

В соответствии с таблицей 3.2 0011₂=3₁₆ и 0001₂=1₁₆.

Тогда 10011₂ = 13₁₆.

1.1.4. Перевод из шестнадцатеричной системы счисления в двоичную:

а) каждая цифра исходного числа заменяется тетрадой двоичных цифр в соответствии с таблицей 3.2.;

б) незначащие нули в результирующем числе отбрасываются.

Пример 1.7. Выполнить перевод числа 13₁₆ в двоичную систему счисления.

По таблице 3.2 имеем: 1₁₆=0001₂; 3₁₆=0011₂.

Тогда 13₁₆ = 00010011₂. После удаления незначащих нулей имеем 13₁₆ = 10011₂.