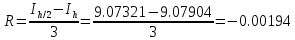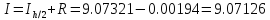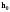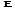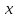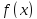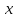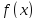Московский Технический Университет

Связи и Информатики

Кафедра Информатики

ОТЧЕТ

по лабораторной работе № 4

«Численное интегрирование»

Отчет подготовил:

студент группы БСТ1401

Балашов И.М.

Вариант № 3

Москва 2015

Задание

1. Выбрать индивидуальное задание из табл. 1.4-1 для численного интегрирования:

• f(x) – подынтегральную функцию;

• a, b– пределы интегрирования;

• метод интегрирования для выполнения п. 2 – значение в столбце t;

• метод интегрирования для выполнения п. 5 – значение в столбце m;

• начальный шаг интегрирования _.

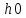При этом значения в столбцах t и m означают: 1 –интегрирование методом средних прямоугольников, 2 – методом трапеций, 3 – методом Симпсона.

2. Составить схему алгоритма и написать программу по выбранному методу численного интегрирования (или по указанному преподавателем), провести контрольное тестирование на примере, разобранном в п. 1.4-5.

3. Вычислить интеграл 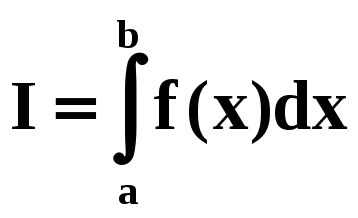с точностью 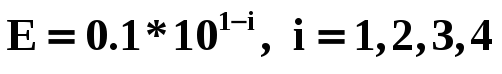и записать результаты вычислений в табл. 1.4-2.

4. Зависимости числа итераций от заданной точности в логарифмическом масштабе.

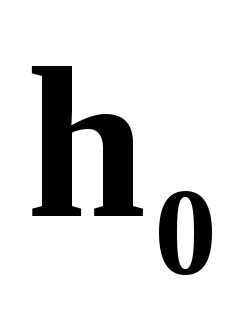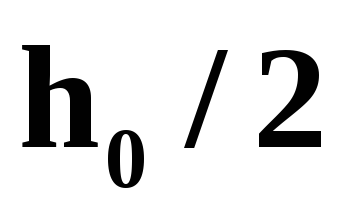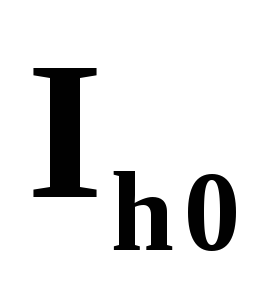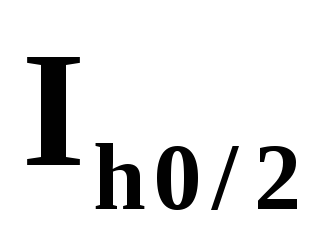5. Вычислить «ручным расчетом» интеграл методом, определяемым значением столбца m из таблицы 1.4-1, с шагом и ( и ) и оценить погрешность по правилу Рунге.

Задание для численного интегрирования

№	f(x)	a	b	t	m
3	x3/2 – 2 x sin(x)	3	4	3	2	0.25

Метод Симпсона - расчёт на ПК

Метод трапеций - ручной расчёт

Решение с помощью математических пакетов

>> syms x

>> int(x^(3/2)-2*x*sin(x),3,4)

ans =

8*cos(4) - 6*cos(3) + 2*sin(3) - 2*sin(4) - (18*3^(1/2))/5 + 64/5

>> 8*cos(4) - 6*cos(3) + 2*sin(3) - 2*sin(4) - (18*3^(1/2))/5 + 64/5

ans =

9.0713

Схемы алгоритмов, программы заданных методов и результаты контрольного тестирования

Метод Симпсона

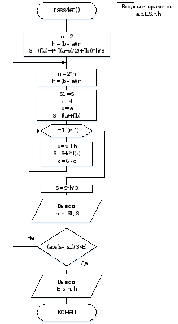
Код программы:

#include<iostream>

#include<conio.h>

#include<math.h>

using namespace std;

float f(float x)

{

return qsrt(x*x*x)-2*x*sin(x);

}

void rass4et(float a, float b, float E, float& S, int& n, float& h)

{

float S1, c, x;

n=2;

h=(b-a)/n;

S=(f(a)+4*f((a+b)/2)+f(b))*h/3;

do

{

n=2*n;

h=(b-a)/n;

S1=S;

c=4;

x=a;

S=f(a)+f(b);

for (int i=1; i<n; i++)

{

x=x+h;

S=S+c*f(x);

c=6-c;

}

S=S*h/3;

cout << "h = "<< h <<"; "<<"n = "<< n <<"; "<<"s1 = "<< S1 <<"; "<<"s = "<< S <<endl;

}

while (abs(S-S1)>=E);

cout<<endl;

}

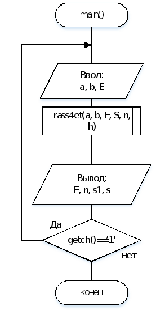
void main()

{

setlocale(0, "");

float S, a, b, E, h;

int n;

do

{

cout<<"Введите значение a: ";

cin>>a;

cout<<"Введите значение b: ";

cin>>b;

cout<<"Введите значение E: ";

cin>>E;

cout<<endl;

rass4et(a,b,E,S,n,h);

cout << "\nРезультаты вычисления: " << endl;

cout << "E = "<< E <<"; "<<"s = "<< S <<"; "<<"n = "<< n <<"; "<<"h = "<< h <<endl;

cout <<endl<< "Для повторения нажмите '1'"<< endl;

}

while(getch()=='1');

}

Результат выполнения программы

E = 0.1

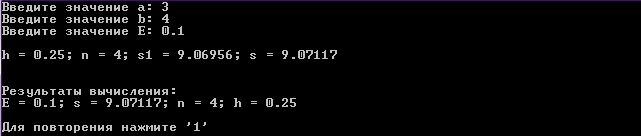
E = 0.01

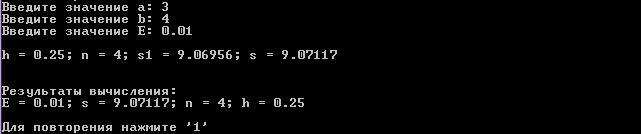
E = 0.001

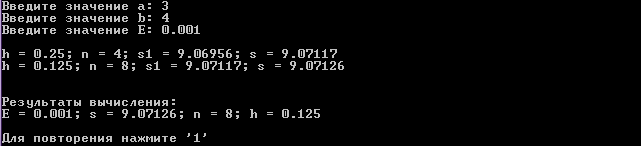
E = 0.0001

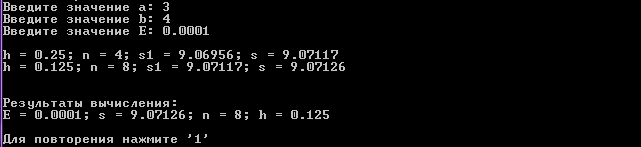
Результаты вычисления

0.1	4	0.25	9.07117
0.01	4	0.25	9.07117
0.001	8	0.125	9.07126
0.0001	8	0.125	9.07126

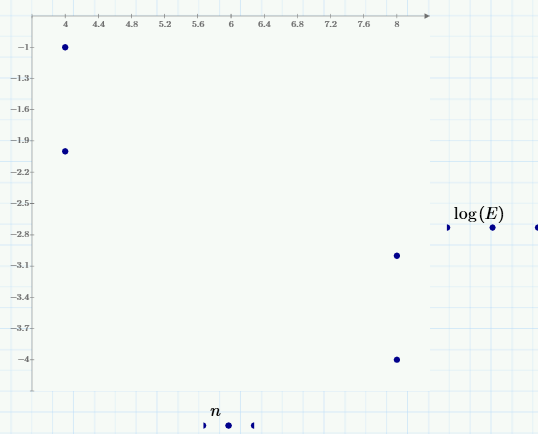
Зависимости числа итераций от точности

E	0.1	0.01	0.001	0.0001
n	4	4	8	8

Ручной расчёт

Метод трапеций

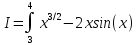
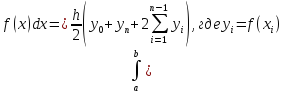
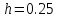
	3	3.25	3.5	3.75	4
	4.34943	6.56229	9.00338	11.54855	14.05442

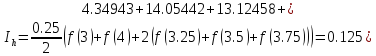
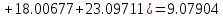
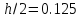
	3	3.125	3.25	3.375	3.5	3.625	3.75	3.875	4
	4.34943	5.42057	6.56229	7.7615	9.00338	10.27159	11.54855	12.81583	14.05442

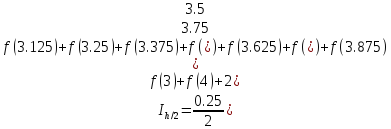
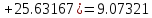
Погрешность по правилу Рунге