
- •1. Цель работы
- •2. Приборы и принадлежности
- •3. Краткие сведения из теории
- •3.1. Основные понятия и законы
- •3.2. Применение основных законов и понятий в лабораторной работе
- •3.2.1. Применение закона сохранения момента импульса
- •3.2.2. Применение закона сохранения энергии
- •3.2.3. Применение теории гармонических колебаний
- •3.2.4. Применение теоремы Штейнера
- •4. Описание экспериментальной установки
- •5. Порядок выполнения работы
- •5.1. Подготовка установки к работе
- •5.2. Определение скорости полета пули
L =[rG, pG] .
Здесь r – радиус-вектор данной материальной точки, p – импульс этой точки, а квадрат-
ными скобками обозначено векторное произведение названных векторов. Поскольку начало координат инерциальной системы можно поместить в любую точку, то по данной формуле можно вычислить момент импульса материальной точки относительно произвольной точки пространства.
Момент импульса материальной точки относительно оси вращения равен
Lz = mvr ,
где r – кратчайшее расстояние от линии скорости материальной точки до этой оси, m – масса этой точки,
v – абсолютная величина скорости точки.
Момент импульса твердого тела относительно неподвижной оси вращения равен
Lz = Jωz ,
где J – момент инерции тела относительно оси вращения, ωz – угловая скорость вращения.
Система называется замкнутой, если тела, входящие в состав системы взаимодействуют между собой и не взаимодействуют с другими телами.
Закон сохранения момента импульса: Момент импульса замкнутой системы остается постоянным относительно любой точки инерциальной системы отсчета.
Удар называют абсолютно неупругим, если после соударения тела движутся вместе как единое целое. При абсолютно неупругом соударении выполняется закон сохранения момента импульса системы. Полная механическая энергия системы в момент удара уменьшается, потому что часть ее переходит во внутреннюю.
3.2. Применение основных законов и понятий в лабораторной работе
3.2.1. Применение закона сохранения момента импульса
В работе рассматривается абсолютно неупругое соударение пули и баллистического маятника. Запишем закон сохранения момента импульса системы «пуля + баллистический маятник»: до соударения - это момент импульса пули относительно оси вращения, после удара – момент импульса баллистического маятника и пули.
mvr = (J1 +mr2 )ω , |
(1) |
здесь m - масса пули, v - её скорость, r - расстояние от оси вращения маятника до точки удара пули, ω - угловая скорость маятника сразу после соударения, J1 - момент инерции маятника.
3.2.2. Применение закона сохранения энергии
После попадания пули в маятник он начинает вращаться относительно вертикальной оси. Если пренебречь при его движении моментом сил трения, то можно использовать закон сохранения энергии. Сразу после попадания пули энергия системы – кинетическая энергия вращательного движения, а в момент максимального закручивания упругой нити – потенциальная энергия упругой деформации кручения.
Из закона сохранения механической энергии после удара следует
1 |
(J1 +mr2 )ω2 |
= |
1 |
Dα2 , |
(2) |
|
2 |
2 |
|||||
|
|
|
|
где α – максимальный угол поворота маятника,
D – постоянная момента упругих сил (модуль кручения нити). Из этих уравнений получаем
4
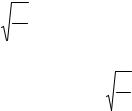
v2 = |
Dα2 |
(J1 +mr2 ) , |
(3) |
|
m2r2 |
||||
|
|
|
Так как момент инерции пули mr2 во много раз меньше, чем момент инерции баллистического маятника J1, то уравнение (3) можно переписать в виде
v2 = |
Dα |
2 J |
1 |
. |
(4) |
m2r2 |
|
||||
|
|
|
|
||
3.2.3. Применение теории гармонических колебаний
При выведении из положения равновесия маятник будет совершать крутильные колебания. При малых углах закручивания подвеса, колебания баллистического маятника являются гармоническими и период определяется по формуле
T |
= 2π J1 . |
(5) |
|
1 |
D |
|
|
|
|
|
|
Формула (5) может быть получена по аналогии с колебаниями пружинного маятника, пери-
од колебаний которого известен из курса средней школы T = 2π |
m |
. Аналогом массы пружин- |
|
k |
|
ного маятника m является момент инерции баллистического маятника J, а аналогом коэффициента жесткости пружины k – постоянная упругих сил D.
Выражая D из (5), получим:
D = |
4π2 J |
1 |
. |
(6) |
T 2 |
|
|||
|
|
|
|
|
|
1 |
|
|
|
Измерив периоды колебаний для двух значений момента инерции маятника, можно исключить неизвестную постоянную D и J1 из (4) и определить скорость пули. Для этого из уравнений
(5) и (6) получим вспомогательные соотношения
|
J1 − J2 |
= |
|
|
J , |
(7) |
||||||||
|
|
|
J |
1 |
|
= |
|
T |
2 |
, |
|
|
||
|
|
|
|
|
|
|
1 |
|
(8) |
|||||
|
|
|
J |
|
|
|
||||||||
|
|
|
2 |
|
|
|
T |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
а из уравнений (7) и (8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J1 |
= |
|
|
|
T 2 |
|
|
|
J . |
|
||||
|
|
|
|
1 |
|
|
|
|
|
(9) |
||||
|
T |
2 |
−T |
2 |
|
|||||||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|||
Здесь J = J1 − J2 – разность момента инерции маятника для двух различных положений |
|
|||||||||||||
грузов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив (5) и (9) в (4), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = |
|
|
|
2παT1 |
|
|
|
J . |
(10) |
|||||
mr(T |
2 |
−T |
|
2 ) |
||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|||
3.2.4. Применение теоремы Штейнера
Величину J можно определить, пользуясь теоремой Штейнера. Из нее следует, что момент инерции баллистического маятника для двух различных положений грузов можно представить как
J1 |
= J0 +2MR12 , |
(11) |
J2 |
= J0 +2MR22 , |
(12) |
где J0 - момент инерции маятника, когда центры тяжести грузов совпадают с осью вращения маятника; J1 - момент инерции, когда оба груза находятся на расстоянии R1 от оси вращения; J2
5
