Умозаключение – прием мышления, посредством которого из исходного знания получается новое знание; из одного или нескольких истинных высказываний, называемых предпосылками, по определенным правилам вывода можно получить заключение.

Пример 5. «Все металлы – простые вещества». «Литий – металл». Следовательно «Литий – простое вещество».

Любое правило вывода умозаключений состоит из двух высказываний (простых или сложных). Одно из них называется предпосылкой или условием, а второе – следствием, заключением или выводом.

Пример 6. «Если треугольник равносторонний, то у него все углы 60 градусов». Высказывание «У него все углы равны 60 градусов» – это заключение, а высказывание «Треугольник равносторонний» – это предпосылка.

Существуют умозаключения, осуществляемые по схемам аналогии, индукции и дедукции.

Умозаключение по аналогии – это правило полученное из рассмотрения какого-либо объекта, переносимое на менее изученный, сходный по существенным свойствам и качествам объекта.

Пример 7. Из высказывания «Солнечная система – это планеты, вращающиеся по орбитам, в центре которых находится Солнце» можно получить умозаключение по аналогии: «Атом – это электроны, вращающиеся по орбитам, в центре которых находится ядро».

Индукция – это правило вывода умозаключений при переходе от частных высказываний к общим.

Пример 8. Высказывания: «кошки имеют хвост», «собаки имеют хвост», «обезьяны имеют хвост», «кошки, собаки, обезьяна – млекопитающие». Следовательно, «все млекопитающие имеют хвост». Это умозаключение ложно.

Индуктивный вывод умозаключений позволяет формулировать различные гипотезы, догадки, но иногда он может приводить и к ошибочным умозаключениям.

Дедукция – это правило вывода умозаключений при переходе от общих суждений к частным.

Пример 9. «Умные люди не делают ошибки». «Я – умный человек». Следовательно: «Я не делаю ошибок».

В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывания можно представить некоторой переменной величиной, значением которой может быть только «0» или «1». Если высказывание истинно, то его значение равно «1», если ложно, то равно «0».

Из уже заданных простых высказываний можно строить более сложные высказывания, используя частицу «не», а также союзы «и», «или», «если..., то...», «тогда и только тогда, когда» и т.п..

2.1. Логические операции

Истинностные значения новых высказываний определяются при этом только истинностными значениями входящих в них высказываний. Построение из данных высказываний (или из данного высказывания) нового высказывания называется логической операцией. Знаки логических операций называются логическими связками. Логические связки могут быть: одноместными (унарными), двухместными (бинарные), трехместными (тернарными) и т.д.

Пример 10.

Из высказываний «х > 2», «х < 3» при помощи связки «и» можно получить высказывание «x > 2 и х < 3»;

из высказываний «у > 10», «х < 3» при помощи связки «или» можно получить высказывание

«у > 10 или х < 3»;

11

из высказываний «х > 2», «у < 3» при помощи связки «если..., то...» можно получить высказывание «если x > 2, то у < 3».

Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями.

В алгебре логики логические операции чаще всего описываются при помощи таблиц истинности. В таблице 1 представлена таблица истинности для операции «отрицание» («инверсия»).

Таблица истинности для операции «отрицания»

Таблица 1

Ане А

В таблице 2 приведены основные бинарные логические операции и связки.

Основные бинарные логические операции и связки

12

Примечание: А1 и А2 являются высказываниями.

Связки и частица «не» рассматриваются в алгебре логики как операции над величинами, принимающими значения 0 (ложь/false) и 1(истина/true), и результатом применения этих операций также являются числа 0 или 1. В таблице 3 представлены все наборы значений переменных А1 и А2 и значения функций на этих наборах.

Таблица истинности для основных бинарных логических операций

Инверсия

Отрицание высказывания А (т.е. не А) обозначается ¬А, или А , или ~ A и часто читается: «отрицание А», «не А» или «А с чертой».

Пример 11. Высказывание А=<Киев-столица Франции>, тогда сложное высказывание НЕ А означает: не верно, что А, т.е. не верно, что <Киев-столица Франции>.

Конъюнкция

Результатом операции конъюнкции для высказывания А В будет истинна только тогда, когда истинны одновременно оба высказывания.

Пример 12. Высказывания А= «Москва – столица России» и В= «Рим – столица Италии». Сложное высказывание А В (А & В) истинно, так как истинны оба высказывания.

Дизъюнкция

Результатом операции дизъюнкции для высказывания А В будет истинна тогда, когда истинно хотя бы одно высказывание, входящее в него.

Пример 13. Высказывания А = «2 + 3 = 5» и В = «3 + 3 = 5». Сложное высказывание: А В (А + В) истинно, так как истинно высказывание А.

Эквиваленция (равнозначность)

Результатом операции эквиваленции для высказывания А ~ В будет истинна тогда, когда истинны или ложны одновременно оба высказывания. Отличие эквиваленции от конъюнкции состоит в том, что вне зависимости от смысла, равнозначными являются как истинные, так и ложные высказывания.

Пример 14. Высказывания А = «2 + 2 = 7» и В = «1 – 8 = 5». Сложное высказывание А ≡ В (А ~ В) истинно, так как оба высказывания ложны.

13

А1 (А2 А3 ) = (А1 А2 ) (А1 А3 ) (закон дистрибутивности).

АА =1 (закон исключенного третьего);

А= А (закон снятия двойного отрицания);

А1 А2 А1 А2 = А1

(А1 А2 )(А1 А2 ) = А1 (закон склеивания);

А1 А2 = А1 А2

А1 А2 = А1 А2 (закон де Моргана);

А1 А1 А2 = А1 А2 (закон свертки).

Эти равенства позволяют существенно упростить запись формул освобождением от лишних скобок.

Пример 19:

Законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами.

Пример 20:

Применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией.

Пример 21:

Повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания.

Пример 22:

Вводится вспомогательный логический сомножитель (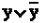); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения.

Пример 23:

15