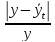2. Рассчитаем средние показатели:
2.1. Средний уровень ряда динамики. Имеем интервальный ряд динамики с равными промежутками времени, поэтому средний уровень ряда определяется по формуле средней арифметической простой:
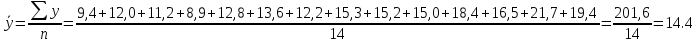 ц/га
ц/га
2.2. Средний абсолютный прирост:
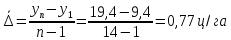
2.3. Средний темп роста:
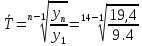 =
=
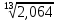 = 1,06 или 106,0%
= 1,06 или 106,0%
2.4. Среднее абсолютное значение 1% прироста:
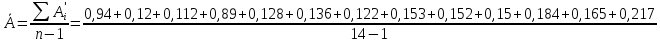 =
=
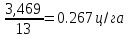
В среднем ежегодно урожайность подсолнуха составляла 14,4 ц/га, в среднем ежегодно увеличивалась на – 0.77ц/га, что в относительном выражении соответствует увеличению в 1,06 раз или на 6%( 106,0%-100%). Каждый процент прироста сопровождался увеличением урожайности подсолнуха около 0.267 ц/га.
3.Аналитическое выравнивание.
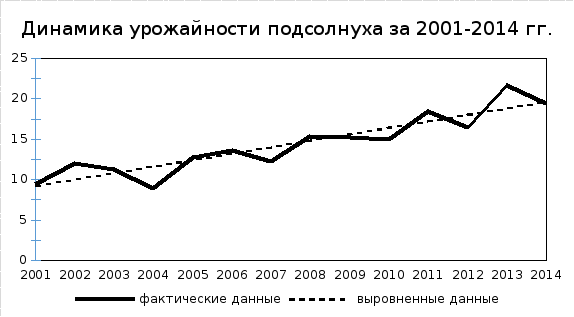
3.1. Для выявления характера динамики урожайности подсолнуха за весь период необходимо построить линейный график по исходным данным (рис.1.1). Основная тенденция кривой по своей форме приближается к прямой линии. Исходя из этого, целесообразно этот ряд динамики выравнивать по уравнению прямой линии (линейного тренда).
Рисунок 1.1
Вспомогательные
расчеты для определения параметров и
и
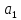 и критерия статистической достоверности
аналитического уравнения
и критерия статистической достоверности
аналитического уравнения
Таблица 2
|
Годы |
Урожайность подсолнуха ц з 1 га |
t |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2001 |
9.4 |
-13.0 |
169 |
-122.2 |
9.2 |
0.2 |
0.021 |
|
2002 |
12.0 |
-11 |
121 |
-132.0 |
10.0 |
2.0 |
0.167 |
|
2003 |
11.2 |
-9 |
81 |
-100.8 |
10.8 |
0.4 |
0.036 |
|
2004 |
8.9 |
-7 |
49 |
-62.3 |
11.6 |
2.7 |
0.819 |
|
2005 |
12.8 |
-5 |
25 |
-64.0 |
12.4 |
0.4 |
0.031 |
|
2006 |
13.6 |
-3 |
9 |
-40.8 |
13.2 |
0.4 |
0.029 |
|
2007 |
12.2 |
-1 |
1 |
-12.2 |
14.0 |
1.8 |
0.265 |
|
2008 |
15.3 |
+1 |
1 |
15.3 |
14.8 |
0.5 |
0.033 |
|
2009 |
15.2 |
+3 |
9 |
49.6 |
15.6 |
0.4 |
0.010 |
|
2010 |
15.0 |
+5 |
25 |
75 |
16.4 |
1.4 |
0.131 |
|
2011 |
18.4 |
+7 |
49 |
128.8 |
17.2 |
1.2 |
0.065 |
|
2012 |
16.5 |
+9 |
81 |
148.5 |
18.0 |
1.5 |
0.136 |
|
2013 |
21.7 |
+11 |
121 |
238.7 |
18.8 |
2.9 |
0.134 |
|
2014 |
19.4 |
+13 |
169 |
252.2 |
19.6 |
0.2 |
0.002 |
|
Всего: |
201.6 |
0 |
910 |
369.8 |
201.6 |
- |
1.879 |
3.2.
Уравнение
прямой имеет вид :
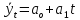 ,
,
где
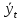 -
выравнивание
(теоретические) уровни ряда динамики;
-
выравнивание
(теоретические) уровни ряда динамики;
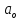 и
и
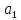 –параметры
уравнения;
–параметры
уравнения;
t – показатель времени, т. е. порядковые номера периодов времени.
3.3.
Если
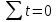 ,
система нормальных уравнений будет
иметь вид:
,
система нормальных уравнений будет
иметь вид:
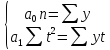 Отсюда
Отсюда
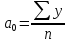
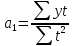
Итак,
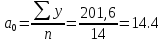
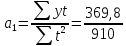 =
0.4
=
0.4
Уравнение прямой имеет вид:
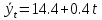 ,
то есть ежегодно урожайность подсолнуха
увеличивалась в среднем на 0,4 ц/га
,
то есть ежегодно урожайность подсолнуха
увеличивалась в среднем на 0,4 ц/га
3.4. С помощью данного уравнения определим теоретические уровни ряда динамики, на основе которых устанавливается тенденция. Для этого подставим значение t в уравнение и получим выровненные (теоретические) значения урожайности подсолнуха(табл.2,гр.6). Величины теоретических уровней отражено на графике (рис.1.1). Результаты позволяют сделать выводы о тенденции увеличения урожайности подсолнуха.
3.5.Проверка точности уравнения на основе относительной ошибки аппроксимации (табл.2, гр.7,8)
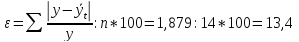
Поскольку ε<15% можно сделать вывод, что в данном случае аналитическое уравнение прямой достаточно точно описывает эмпирические данные.