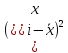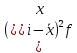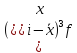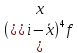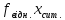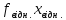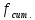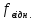лрстатистика
.docxВариант №21
1. Содержание задания
(для студентов всех специальностей)
1. С помощью аналитической группировки с равными интервалами и определите наличие зависимости между результативным и факторным признаками (lg20 = 1,3). Сделайте выводы относительно зависимости между показателями.
2. Проведите структурную группировку совокупности по факторным признаком.
Сделайте выводы.
3. По интервальным вариационным рядом факторного признака рассчитайте:
а) показатели центра распределения: среднее значение, моду и медиану;
б) показатели структуры распределения: первый, девятый децілі и коэффициент децільної дифференциации, коэффициент Джини;
в) показатели вариации: дисперсию и коэффициент вариации;
г) показатели формы распределения: коэффициенты асимметрии и эксцесса.
По каждому подпункту задачи сделайте выводы. Варианты заданий содержатся в таблице 1 приложения.
Исходные данные:
|
№ предприятия |
Стоимость активной части основных фондов предприятия, млн.грн. |
Выпуск продукции, млн.грн. |
|
1 |
26 |
20 |
|
2 |
25 |
18 |
|
3 |
20 |
21 |
|
4 |
30 |
29 |
|
5 |
34 |
35 |
|
6 |
28 |
30 |
|
7 |
27 |
24 |
|
8 |
30 |
31 |
|
9 |
31 |
38 |
|
10 |
29 |
35 |
|
11 |
35 |
40 |
|
12 |
26 |
38 |
|
13 |
37 |
35 |
|
14 |
35 |
41 |
|
15 |
41 |
48 |
|
16 |
39 |
43 |
|
17 |
38 |
49 |
|
18 |
40 |
51 |
|
19 |
45 |
50 |
|
20 |
43 |
55 |
1.Рассчитываем число групп по формуле Старджесса:
L = 1+2.233lgn = 1+ 2.233lg20 = 4
Тогда величина интервала группировки по факторному признаку Х
« стоимость активной части основных фондов предприятия» равна:
 =
(45-20)/4 = 6.25 млн.грн.
=
(45-20)/4 = 6.25 млн.грн.
тогда интервалы будут такими:
20 - 26.25
26.25 – 32.5
32.5 – 38.75
38.75 – 45.0
Составляем структурную группировку предприятий по признаку «стоимость активной части основных фондов предприятий»
|
№ п.п. |
Группы предприятий по стоимости активной части основных фондов,млн.грн |
№№ предприятий |
Стоимость активной части основных фондов, млн.грн. |
Выпуск продукции, млн.грн. |
|
I |
20.0 – 26.25 |
3 |
20 |
21 |
|
2 |
25 |
18 |
||
|
1 |
26 |
20 |
||
|
12 |
26 |
38 |
||
|
Итого: |
4 |
97 |
97 |
|
|
II |
26.25 – 32.5 |
7 |
27 |
24 |
|
6 |
28 |
30 |
||
|
10 |
29 |
35 |
||
|
8 |
30 |
31 |
||
|
9 |
31 |
38 |
||
|
4 |
30 |
29 |
||
|
Итого: |
6 |
175 |
187 |
|
|
III |
32.5 – 38.75 |
5 |
34 |
35 |
|
11 |
35 |
40 |
||
|
14 |
35 |
41 |
||
|
13 |
37 |
35 |
||
|
17 |
38 |
49 |
||
|
Итого: |
5 |
179 |
200 |
|
|
IV |
38,75 – 45,0 |
16 |
39 |
43 |
|
18 |
40 |
51 |
||
|
15 |
41 |
48 |
||
|
20 |
43 |
55 |
||
|
19 |
45 |
50 |
||
|
Итого: |
5 |
208 |
247 |
Из расчетных данных прослеживается прямая зависимость между стоимостью активной части основных фондов предприятия (факторный признак х) и выпуском продукции (результативный признак у). Так с увеличением стоимости активной части основных фондов предприятия по каждой группе увеличивается соответственно выпуск продукции
Составляем аналитическую группировку предприятий по признаку «стоимость активной части основных фондов»
|
№ п.п. |
Группы предприятий по стоимости активной части основных фондов, млн.грн. |
Число предприятий |
Стоимость активной части основных фондов, млн.грн. |
Выпуск продукции, млн.грн. |
||
|
Всего |
В среднем |
Всего |
В среднем |
|||
|
I |
20.0 – 26.25 |
4 |
97 |
24.3 |
97 |
24.3 |
|
II |
26.25 – 32.5 |
6 |
175 |
29.2 |
187 |
31.2 |
|
III |
32.5 – 38.75 |
5 |
179 |
35.8 |
200 |
40 |
|
IV |
38.75 – 45.0 |
5 |
208 |
41.6 |
247 |
49.4 |
|
|
№ п.п. |
Группы предприятий по стоимости активной части основных фондов, млн.грн |
Кол-во пр-й
|
( |
|
( |
|
|
|
|
|||||||||||||||||
|
I |
20.0 – 26.25 |
4 |
23.2 |
92.4 |
-9.7 |
94.09 |
376.4 |
-3650.692 |
35411.7124 |
||||||||||||||||||
|
II |
26.25 – 32.5 |
6 |
29.4 |
176.4 |
-3.4 |
11.56 |
69.4 |
-235.824 |
801.8016 |
||||||||||||||||||
|
III |
32.5 – 38.75 |
5 |
35.6 |
178.0 |
2.8 |
7.84 |
39.2 |
109.76 |
307.328 |
||||||||||||||||||
|
IV |
38.75 – 45.0 |
5 |
41.9 |
209.5 |
9.1 |
82.81 |
414.05 |
3767.855 |
34287.4805 |
||||||||||||||||||
|
Итого: |
20 |
- |
626.9 |
- |
- |
899.05 |
-8.901 |
70808.3225 |
|||||||||||||||||||
С увеличением стоимости активной части основных фондов предприятия наблюдается рост выпуска продукции.
I:
II:
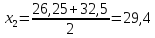 , III:
, III:
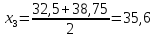 ,
IV:
,
IV:
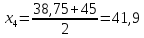
Рассчитываем среднюю стоимость основных фондов предприятия:
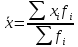 =
626,9/20 = 31,3 млн.грн.
=
626,9/20 = 31,3 млн.грн.
Рассчитываем моду:
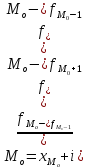 =
26,25+6,25
=
26,25+6,25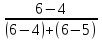 = 30,42 млн.грн.
= 30,42 млн.грн.
Большинство предприятий имеют стоимость основных фондов в размере 30,42 млн.грн.
Рассчитаем медиану:
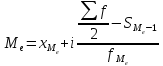 =
26,25+6,25
=
26,25+6,25 = 32,5 млн.грн.
= 32,5 млн.грн.
У половины предприятий, стоимость активной части основных фондов не превышает 32,5 млн. грн., а у другой половины предприятий, стоимость активной части основных фондов, стоимость соответственно выше 32,5 млн.грн.
Вычисляем дисперсию:
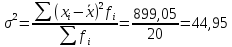
Находим среднеквадратическое отклонение:
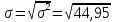 =
6,7 млн.грн.
=
6,7 млн.грн.
Находим коэффициент вариации:
V
=
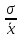 *100% =
*100% =
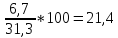
Из расчетных данных среднеквадратического отклонения и коэффициента вариации можно сказать, что совокупность предприятий относительно стоимости основных фондов предприятий однородная, средняя типична и ей можно доверять.
Децильный коэффициент дифференциации стоимости активной части основных фондов предприятий, характеризующийся, во сколько раз минимальная стоимость 10% стоимости активной части основных фондов предприятий превышают максимальную стоимость 10% стоимости активной части основных фондов предприятий:
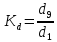 ,
где
,
где
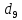 – девятый дециль распределения;
– девятый дециль распределения;
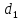 – первый
дециль распределения.
– первый
дециль распределения.
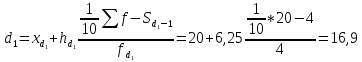 млн.грн.
млн.грн.
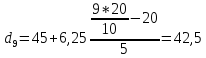 млн.грн.
млн.грн.
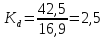 ,
т.е. значение коэффициента означает,
что в 2,5 раза минимальная стоимость 10%
предприятий стоимости активной части
основных фондов, что имеют наибольшую
стоимость, выше стоимости основных
фондов 10% предприятий, что имеют наименьшую
стоимость активной части основных
фондов.
,
т.е. значение коэффициента означает,
что в 2,5 раза минимальная стоимость 10%
предприятий стоимости активной части
основных фондов, что имеют наибольшую
стоимость, выше стоимости основных
фондов 10% предприятий, что имеют наименьшую
стоимость активной части основных
фондов.
Для количественной оценки уровня концентрации рассчитываем коэффициент концентрации Джини:
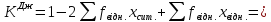 1-2*0,05605+0,0254355
= 0,913
1-2*0,05605+0,0254355
= 0,913
Коэффициент Джини приблизился к единице, что свидетельствует о значительном расслоении стоимости основных фондов предприятий.
Таблица «Кумулятивные показатели распределения предприятий по стоимости активной части основных фондов.»
|
Стоимость активной части основных фондов,млн.грн. |
Число предприятий, f |
Число предприятий |
Общая сумма стоимости основных фондов |
|
|
||||||||
|
Интервальное распределение |
Дискретные значения, х |
Накопленная частота
|
частость,%,
|
Накопленная частота,% |
млн.грн xf |
в % итоге
|
накопленная в % итоге
|
|
|
||||
|
20.0 – 26.25 |
23.1 |
4 |
4 |
2 |
2 |
92.4 |
14.74 |
14.74 |
0,002948 |
0,002948 |
|||
|
26.25 – 32.5 |
29.4 |
6 |
10 |
3 |
5 |
147.0 |
23.45 |
38.19 |
0,011457 |
0,007035 |
|||
|
32.5 – 38.75 |
35.6 |
5 |
15 |
2.5 |
7.5 |
178.0 |
28.39 |
66.58 |
0,016645 |
0,0070975 |
|||
|
38.75 – 45.0 |
41.9 |
5 |
20 |
2.5 |
10.0 |
209.5 |
33.42 |
100 |
0,025 |
0,008355 |
|||
|
Итого: |
- |
20 |
- |
10 |
- |
626.9 |
100 |
- |
0,05605 |
0,0254355 |
|||
Рассчитываем показатель асимметрии через отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе, то есть
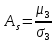
где
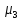 – центральный момент третьего порядка,
рассчитываем по формуле
– центральный момент третьего порядка,
рассчитываем по формуле
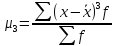
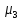 =
-8.901/20 = -0.44505
=
-8.901/20 = -0.44505
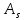 =
-0,44505/
=
-0,44505/ = -0,0015
= -0,0015
Так как величина асимметрии отрицательна, следовательно, речь идет о левосторонней асимметрии.
Далее рассчитаем показатель эксцесса. Наиболее точно он определяется по формуле с использованием центрального момента четвертого порядка
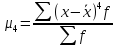
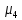 =
70808,3225/20 = 3540,416
=
70808,3225/20 = 3540,416
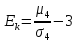
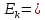 70808,3225/
70808,3225/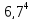 – 3 = 32,14
– 3 = 32,14
Так
как
 распределение является островершинным.
распределение является островершинным.

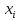 )
)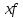
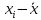 )
)