13. Обработка прямых многократных измерений.

1. Из результатов наблюдений исключают известные систематические погрешности.

2. Если есть подозрение о наличии грубых погрешностей, то проверяют гипотезу по критерию t_Г. Для этого находят значение среднего арифметического А_ср, исключив из него систематическую погрешность, значение среднего квадратического отклонения σ^*_Δ, а далее вычисляют t_Г1=(A_cp-A_nmin)/σ^*_v ; t_Г2=(A_nmax-A_cp)/σ^*_v

Значения t_Г1 и t_Г2 сравнивают с табличным t_Г. Если t_Г1 и t_Г2 больше t_Г, то A_nmin и A_nmax исключают из дальнейшей обработки.

3. Вычисляют А_ср, σ^*_v σ^*_Acp исправленных результатов наблюдений.

σ^*_Acp = σ^*_v/√n’ .4. Если распределение подчин-ся нормальному з-ну, то задаётся довер вер-тью α и по ней находят β, Δ_α или t_c, Δ_α Δ_α=2β· σ^*_Acp где β - табличная величина, значение аргумента интеграла вероятности Ф(β);

5. определяют границы неисключенной систематической погрешности Q – погрешности обусловленные классом точности прибора. Для абсолютной погрешности Q=Δ=A₀-A_n=±α. Для относительной погрешности Q=±(δ/100)·A_cp Для привидённых Q = (γ/100)A_cp

Если имеется несколько неучтённых погрешностей необходимо найти: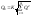

где m – число погрешностей;

К = 1,1 при доверительной вероятности α=0.95.

6. Определяют отношение Q_Σ/σ^*_Acp. Если оно меньше 0,8, то неисключенными погрешностями пренебрегают.

Если оно больше 8, то пренебрегают случайной погрешностью и считают, что Δ=2θ_Σ.

Если 0,8 < θ_Σ/σ^*_Acp < 8, то при определении границ погрешности нужно учитывать и случайную и систематическую составляющие. Δ_Σ=K’·σ_Σ, где , .

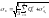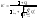
Результат измерения и погрешности представляют в виде A₀=(A_cp±Δ_Σ); α.

14. Погрешности косвенных измерений.

При косвенных измерениях искомая величина А функционально связана с другими величинами - x, y,…t, которые и подвергаются прямым измерениям. Поэтому и абсолютная погрешность величины Δ_А является некоторой функцией погрешностей прямых измерений ∆_A=F(∆_x, ∆_y, ∆_t)

Например, для случая одной переменной А=f(x). В результате измерения получим

A+ Δ_А=f(x+Δ_x). (4.23) Разложим правую часть (4.23) в ряд Тейлора и сохраним члены разложения, содержащие Δ_x в первой степени. Тогда . (4.24) Это выражение показывает что А=f(x).Δ_A=±df(x)·∆_x/dx

В общем случае абсолютная погрешность находится геометрическим суммированием:

,

где слагаемые – квадраты частных погрешностей прямых измерений.

Прямые измерения величин x, y,…t могут выполняться путем многократных наблюдений, с определением точечных оценок x_cp,y_cp,…t_cp, а также 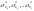. Тогда оценка среднеквадратического значения абсолютной погрешности косвенных измерений определяется формулой

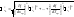
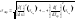Появились остаточные значения.

9. Доверительные интервалы.

Рассмотренные оценки результатов измерений A_cp;σ^*_Acp;σ_Δ^* выражаются одним числом и называются точечными. Так как такую оценку принимают за действительное значение измеряемой величины, то встает вопрос об её точности и надежности. Судят об этом по вероятности α того, что абсолютная величина отклонения Δ_сл=А₀-А_ср будет оставаться меньше некоторой назначенной величины ε: Р(|Δ_сл|)≤ε=α (4.16)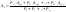

или Р(А₀-А_ср ||)≤ε=α (4.17) В (4.17) величина ε характеризует точность, а α надежность оценки. Поэтому вероятность α называют доверительной вероятностью.

Равенство (4.17) можно переписать в виде P(A_cp-ε≤A₀≤A_cp+ε)=α (4.18) Выражение (4.18) показывает, что интервал Δ_α=2ε с вероятностью α накрывает величину A₀. Поэтому его называют доверительным интервалом. Подставим в выражение (4.16) нормированные величины: X=Δ_сл/δ_Δ и β=ε/δ_Аср

Тогда можно записать известное из теории вероятностей равенство Р(-β≤X≤β)=F(β)-F(-β)=α (4.19) Значит, если известна функцияF(x), то конкретное значение α определяет значение β и наоборот. Кроме того, из сопоставления (4.19) и (4.6) получаем равенство α=Ф(β). (4.20) С учетом изложенного определение интервальной оценки можно выполнить в следующем порядке.

1. По результатам измерений вычисляют.A_cp;σ^*_Acp;σ_v^* 2. Задают доверительную вероятность α , обычно α>0.9. 3. По таблице интеграла вероятности Ф(х) находят при Ф(х) =α значение X. Это значение принимают равным β.

Так как β=ε/ σ^*_Acp, то ε=β· σ^*_Acp a Δ_α=2ε. При малом числе измерений 2 < п < 20 доверительный интервал должен быть расширен. С этой целью вместо коэффициента β в (4.21) используют коэффициент Стьюдента t_cm. Его значения рассчитаны для различных п и α. Результаты расчетов табулированы.

Обратная задача – определение α по Δ_α Ф(β)=α=2F(β)-1=2F([ε/ σ^*_Acp]-1) где ε/ σ^*_Acp=β. При п < 20 α=2F(t_cm)-1=2(ε/ σ_Acp)-1, где ε/ σ_Acp= t_cm В ряде случаев закон распределения погрешности неизвестен, но известны числовые характеристики A_cp;σ^*_Acp;σ_v^* . В этих случаях для грубой оценки снизу доверительной вероятности α при заданном доверительном интервале Δ_α=2ε можно воспользоваться неравенством Чебышева α=P(|A₀-A_cp|≤ε)≥1-σ^*2_Acp/ε². (4.22) Используя неравенство Чебышева легко определить доверительный интервал, если задана доверительная вероятность α≥1- σ^*2_Acp/ε² ; → σ^*2_Acp/ε²≥1- α ; (σ^*2_Acp)/1- α) ≥ ε² откуда ∆_α=2ε ≤ 2σ^*2_Acp/(√1- α) .