25. Индукционный счетчик электрической энергии. Принцип действия и устройство.

Предназначен для учета активной энергии потребляемой нагрузки. Основными частями являются катушка тока, катушка напряжения, легкий алюминиевый диск, который может вращаться вокруг вертикальной оси. Катушки намотаны на ферромагнитный сердечники с прорезями для дисков. Работает только в цепи переменного тока. Для нормальной работы счетчика его диск должен вращаться с постоянной угловой скоростью, пропорциональной активной энергии, потребляемой нагрузкой. При этом формула счетчика: W=C₀N, где С₀ – номинальная постоянность счетчика из его паспортных характеристик, N – количество оборотов диска за время t.

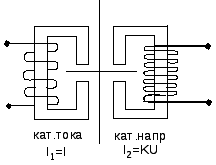
26.Вывод формулы счетчика.

Вращающий момент диска: М_вр=KIUcosφ. Противовращающий момент, необходимый для равномерного вращения диска, создается включением постоянного магнита, силовые линии которого пересекают вращающий диск. Благодаря действию силы Ампера возникает магнитное торможение диска и противовращающий момент: М_пр.вр.=K₁w. Приравняем: Kp=K₁w (умножим все на t) → pt=K₂wt → (N=φ/2π) → K₂2π=C_H → W_сч=C_HN.

27.Определение параметров комплексной нагрузки.

В качестве такой нагрузки могут быть использованы: реальный конденсатор или катушка индуктивности. Каждый из этих элементов имеет некоторое активное сопротивление потерь. В качестве Z_H используется катушка индуктивности X_L; если отключить лампу накаливания, то ток через реактивный элемент будет малым по величине, поэтому вначале включается лампа накаливания, измеряется ток через лампу, а затем включается реактивный элемент и измеряется общий ток, тогда разность этих токов даст ток через катушку. Ток и напряжение на реактивном элементе известны. Определим cosφ из треугольника сопротивлений. В итоге придем к выводу, что

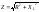
28. Погрешность, вносимая амперметром в измерение тока.

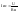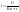
При протекании тока по нагрузке амперметр даёт показания. ,Погрешность, вносимая амперметром будет меньше, если меньше внутреннее сопротивление амперметра.

29. Погрешность, вносимая вольтметром в измерение напряжения.

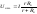
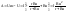Истинное значение напряжения найдется в случае, если вольтметр будет выключен: . При подключении вольтметра значение тока амперметра изменится: ^и

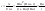
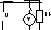
32.Измерение активного сопротивления по методу амперметра и вольтметра.

Возьмем для измерений амперметр с достаточно малым внутренним сопротивлением. Тогда вольтметр будет показывать входное напряжение Uv=U. В узле 1 происходит разделение неразделенного тока I, показанного амперметром на ток Iх и ток вольтметра Iv. Вольтметр и неизвестное сопротивление Rx включены параллельно, поэтому их общее сопротивление будет равно 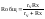По закону Ома для участка 1-2 можно записать:U=I*R_общ.

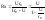
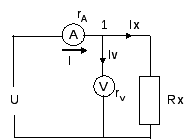
33.Измерение активного сопротивления методом вольтметра.

При замыкании ключа в положение 1 вольтметр измерит входное напряжение U (U_v1=U). При замыкании ключа в положение 2 показание вольтметра изменится и станет равным U_v2. При этом через вольтметр и неизвестное сопротивление Rх будет протекать одинаковый ток I. По закону Ома можно записать: U=U_v2+IRx;; Подставив 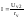мы в итоге получим:

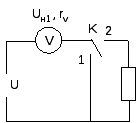
34. Измерение активного сопротивления методом амперметра и известного активного сопротивления R₀.

При включении ключа в положение 1 амперметр будет показывать некоторый ток I₁, который по закону Ома будет связан с входным напряжением U по формуле: U=I₁r_A+I₁R_0. При включении ключа в положении 2 амперметр покажет значение тока I₂, которое будет связано с входным напряжением по формуле: U=I₂r_A+I₂R_х. Приравняв и выразив Rx, получим:

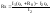
35. Мост Уитстона для измерения активного сопротивления

В одну диагональ моста подключается источник постоянного напряжения U, а во вторую часть моста - гальванометр (прибор для измерения малых токов). Одно из сопротивлений R₁ берётся переменным. Зададимся произвольным направлением токов в ветвях схемы. С помощью переменного резистора R, добиваемся условия равновесия моста при котором ток в цепи гальванометра становится равным нулю Ir=0. Это условие будет выполнено, когда φb=φd. При выполнении этого условия I₁=I₂ и

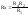
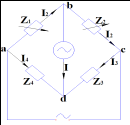
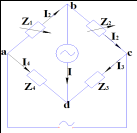
37. Одинарный мост переменного тока.

Для приведения моста переменного тока нужны две регулировки (Z1 и Z2). Условие равновесия моста: 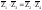.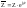-экспоненциальная форма записи.

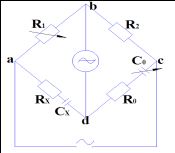
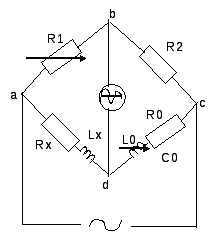
38 Мост Сотти для определения характеристик параметров конденсатора.

R₀- известное активное сопротивление и C₀- известный магазин ёмкостей. Условие равновесия: Условие равновесия в общем виде: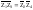Найдем С_х и R_x.

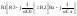
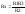
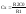
39. Мост Винна для определения параметров катушки индуктивности.

Rx – активное сопротивление провода катушки, Lx – неизвестная индуктивность катушки. Условие равновесия в общем виде: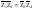НайдемL_х и R_x.

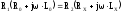
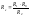
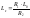
40 Измерение частоты гармонического напряжения с помощью осциллографа и фигур Лиссажу.

х, у– входы осциллографа. у есть у всех (штекер), а вот х не у всех. Если на вход у подаётся синусоидальное напряжение неизвестной частоты: U(t)=U₀ sin ωt, а на х ничего не будем подавать, то увидим вертикальный отрезок 2U₀. Для того чтобы получить реальную зависимость от времени исследуемого напряжения, подаем напряжение на х.

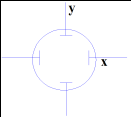
Лиссажу: такие характерные фигуры вычерчивает электронный луч при определенных соотношениях между частотами синусоидальных напряжений на входах х и у. Простейшей фигурой явл-ся эллипс. Уравнение фигуры Лиссажу: