3.6. Погрешности косвенных измерений

Анализ погрешностей косвенных измерений в большинстве случаев заключается в расчете числовых характеристик погрешности определения измеряемой величины по заданным характеристикам погрешностей измерений аргументов.

Если известны истинные значения аргументов , то истинное значение величины, измеряемой косвенным методом, будет:

(3.34)

но результаты прямых измерений известны с погрешностями:

значит

если

(погрешности малы),

то разложим (3.35) в ряд Тейлора:

(3.36)

систематическая погрешность:

т.к. - систематическая плюс случайная составляющие,

то

; ;;(3.37)

В линейном случае, когда - линейная функция:

(3.38)

Нелинейная поправка:

(3.39)

зависит не только от систематических погрешностей аргументов, но и их случайных погрешностей. В случае малых погрешностей измерений поправку можно не учитывать.

Для оценки случайной погрешностей измерений необходимо вычесть (3.37) из (3.36) и пренебречь членами, содержащими квадраты погрешностей:

Возводим это равенство в квадрат, и находя математическое ожидание от его обеих частей, имеем:

Тогда:

(3.40)

Для независимых погрешностей :

(3.41)

Частные случаи:

, =>

;

- относительные систематические погрешности;

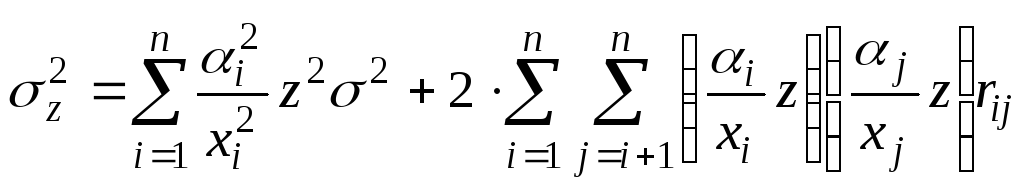
Пример 1.По результатам прямых измерений емкостииопределена емкость. Найти погрешности её измерения, если заданы,,,,. Согласно (3.38) и (3.41) систематическая и случайная погрешности будут:

Вводится поправка, для направления результата:

Для доверительной вероятности ,:

, =>

СКО:

, при .

В нашем примере ,!

Рассмотрите случай, когдаr₁₂=1?

Пример 2.По результатам измерения напряженияи сопротивлениекосвенным методом измерена мощность. Определить погрешности её измерения, если,.

По формулам для произведения:

Относительно СКО:

Мощность ;

; ;;

Результат измерений: