3. Определение доверительного интервала для средней величины внешнеторгового оборота фирм в генеральной совокупности

Величина доверительного интервала (предельная ошибка выборки) находится из выражения

, (40)

где t – коэффициент доверия;

- средняя ошибка выборки.

Средняя ошибка бесповторной выборки:

, (41)

где - дисперсия генеральной совокупности;

- объем выборочной совокупности;

N – объём генеральной совокупности.

В случае малой выборки (n<100) средняя ошибка бесповторной выборки находится из выражения:

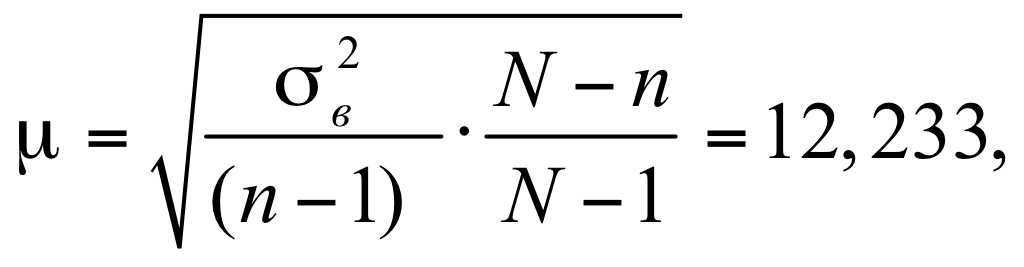(42)

где

Коэффициент доверия в распределении Стьюдента является функцией доверительной вероятности и функцией объема выборки. Его значение получим с помощью функции СТЬЮДЕНТ.ОБР.2Х (0,05; 47), где 0,05 – уровень значимости, n-1=47- количество степеней свободы.

.

Выборка считается репрезентативной, если величина ее относительной ошибки составляет не более 5%, т.е.

(43)

Учитывая, что , выборку следует признать представительной.

4. Анализ зависимости таможенных платежей от внешнеторгового оборота фирм

4.1 Построение групповой таблицы.

Для построения групповой таблицы вычисляются средние значения результативного признака в каждой группе фирм (графа 6 табл. 5.2). Сравнив их значения, можно предположить о наличии прямой корреляционной зависимости между признаками, что иллюстрируется рис. 4.

Рис. 4. Зависимость средних перечислений в бюджет

от среднего значения ВТО фирм

4.2. Проверка правила сложения дисперсий и оценка степени влияния факторного признака на величину результативного.

Правило сложения дисперсий заключается в равенстве общей дисперсии сумме средней из внутригрупповых и межгрупповой дисперсий, т.е.:

, (44)

где, (45)

—общая средняя арифметическая результативного признака;

_ среднее значение результативного признака в - ой группе;

- cредняя из внутригрупповых дисперсий;

—дисперсия в j-ой группе (графа 13 табл. 5.2), вычисляемая по формуле:

;

- межгрупповая дисперсия;

Как следует из выражения (44) правило сложения дисперсий выполняется.

Разделив левую и правую части выражения (44) на общую дисперсию получим следующее тождество:

доли средней из внутригрупповых и межгрупповой дисперсий в сумме равны единице.

Второе слагаемое именуется эмпирическим коэффициентом детерминации (причинности) и обозначается

(46)

Квадратный корень из коэффициента детерминации принято называть корреляционным отношением:

(47)

Изменяется корреляционное отношение от 0 до 1.

При недостаточном количестве данных в выделенных группах к рассчитанной величине корреляционного отношения вносится поправка:

, (48) где m — число выделенных групп.

Для оценки значимости корреляционного отношения можно применить однофакторный дисперсионный анализ. Его логика рассуждений сводится к следующему:

Пусть - математическое ожидание результативного признака, соответственно в группах. Если при изменении уровня фактора групповые математические ожидания не изменяются, то результативный признак не зависит от фактора А - в противном случае такая зависимость имеется.

В связи с тем, что числовые значения математических ожиданий неизвестны, то возникает задача проверки гипотезы

Проверить данную гипотезу можно при соблюдении следующих требований при каждом значении уровня фактора:

1. наблюдения независимы и проводятся в одинаковых условиях;

2. результативный признак имеет нормальный закон распределения с постоянной для различных уровней генеральной дисперсией.

Для ответа на второй вопрос вычислим значения относительных показателей асимметрии и эксцесса для зависимой переменной. Учитывая, что каждый из них меньше 1,5 эмпирическое распределение таможенных платежей в бюджет не противоречит нормальному.

Проверим выполнение гипотезы:

(49)

с помощью критерия Бартлетта:

где остаточная дисперсия, что является синонимом средней из внутригрупповых выборочных дисперсий;

выборочная дисперсия в ой группе (графа 14 табл. 5.2); ;

;

.

При выполнении гипотезы о равенстве дисперсий, величина w имеет распределение близкое к сстепенями свободы.

При соблюдении условия

гипотеза (7.14) подтверждается.

Здесь - правосторонняя критическая точка при заданном уровне значимости, определяющая критический интервал ().

Далее можно приступить к проверке гипотезы . Для этого сформируем массив значений результативного признака по группам (табл. 4).

Массив значений результативного признака

Таблица 4

Обратимся к режиму работы «Однофакторный дисперсионный анализ».

Однофакторный дисперсионный анализ
ИТОГИ						Таблица 5
Группы	Счет	Сумма		Среднее		Дисперсия
Столбец 1	5	72,29		14,46		1,566
Столбец 2	12	202,05		16,84		0,721
Столбец 3	14	272,83		19,49		0,780
Столбец 4	11	238,77		21,71		1,210
Столбец 5	6	146,02		24,34		1,892
Дисперсионный анализ													Таблица 6
Источник вариации	SS	df		MS		F			P-Значение			F критическое
Между группами	405,746	4		101,437		95,066			9,022E-21			2,589
Внутри групп	45,882	43		1,067
				102,504
Итого	451,628	47		9,609

Проверка гипотезы о равенстве математических ожиданий основывается на сравнении оценок факторной и остаточнойдисперсий. В математической статистике доказывается, что если гипотеза о равенстве математических ожиданий подтверждается, то величина

имеет F – распределения с числом свободы и, т.е.

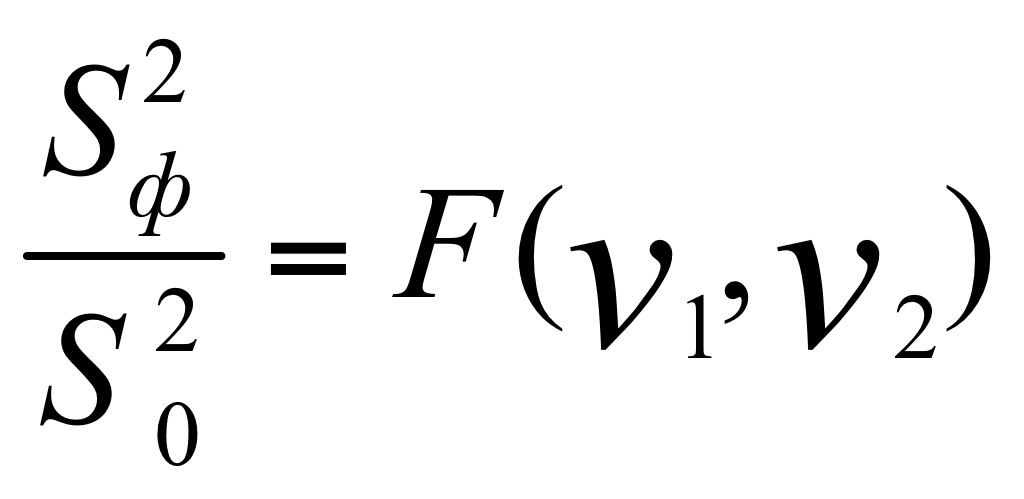, где ;

При использовании F – критерия строится правосторонняя область (), т.к. обычно. Если расчетное значениеF – критерия попадает в указанный интервал, то гипотеза о равенстве групповых математических ожиданий отвергается, т.е. считаем, что факторА влияет на результативный признак Y и можно измерить степень этого влияния с помощью корреляционного отношения.

4.3. Оценка степени взаимной согласованности между суммой

внешнеторгового оборота фирм и величиной таможенных платежей в бюджет с помощью линейного коэффициента корреляции, проверка его значимости и возможности использования линейной функции в качестве формы уравнения

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции (); при любой форме зависимости (линейной и криволинейной) - эмпирическое корреляционное отношение ()).

Для расчета линейного коэффициента корреляции можно использовать формулу:

, (50)

где — среднее значение произведения факторного и результативного признаков;

- средние значения факторного и результативного признаков;

n— число единиц в совокупности;

—средние квадратические отклонения соответственно признака - фактора и результативного признака.

Оценка существенности линейного коэффициента корреляции при большом объеме выборки (свыше 500) проводится с использованием отношения коэффициента корреляции () к его средней квадратической ошибке ():

, (51)

где . (52)

Если это отношение окажется больше критического значения t-критерия Стьюдента, определяемого по формуле СТЬЮДЕНТ.ОБР.2X(0,95;46) при числе степеней свободы к = п - p - 2 и с вероятностью (1 — ), то следует говорить о существенности коэффициента корреляции (— уровень значимости 0,01 или 0,05; p - количество факторных признаков).

При недостаточно большом объеме выборки величину средней квадратической ошибки коэффициента корреляции определяют по формуле

. (53)

В этом случае . (54)

Полученная величина сравнивается с критическим значениемt-критерия Стьюдента ().

В тех случаях, когда получен по данным малой выборки и близок к единице (> 0,8), для построения доверительного интервала коэффициент корреляции преобразуют в величину, имеющую приблизительно нормальное распределение и рассчитываемую по формуле

(55)

Данное выражение имеет название «z – преобразование Фишера».

Интервальная оценка для z определяется из выражения

(56)

где - табулированые значения для стандартного нормального распределения, зависимые от. На основе обратногопреобразования Фишера определяется интервальная оценка линейного коэффициента корреляции.

Приведем реализацию изложенного алгоритма.

• по формуле ФИШЕР() – вычисляется значение ;

• по формулам

2,196-НОРМСТОБР((0,95+1)/2)*КОРЕНЬ(1/45)=1,904 и

2,196+НОРМСТОБР((0,95+1)/2)*КОРЕНЬ(1/45)=2,489 рассчитываются интервальные оценки z;

• по формулам ФИШЕРОБР(1,904)=0,957 и ФИШЕРОБР(2,489)=0,986 находим обратные преобразования Фишера.

Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от 0,957 до 0,986.

Средняя квадратическая ошибка Z'-распределения зависит только от объема выборки и определяется по формуле:

. (57)

Если соотношение Z' к средней квадратической ошибке (Z': =14,42) окажется больше критического значения критерия Стьюдента при определенном уровне значимости, то можно говорить о наличии связи между признаками в генеральной совокупности.