
Лабораторные работы по теме Молекулярная физика. Номера 67, 70, 71, 78
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ ПОВОЛЖСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ КАФЕДРА ФИЗИКИ
МЕТОДИЧЕСКАЯ РАЗРАБОТКА к выполнению лабораторных работ по теме
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
для студентов второго курса дневной и заочной форм обучения по специальностям 210406, 210406у, 210404, 210404у, 210403, 210302,
210405, 230105, 230201, 73с
Составители: к.ф.-м.н., доцент Агапова Н.Н. ст.пр. Арсеньев А.Н.
ст.пр. Топоркова Л.В. инж. Михалькова О.Е.
Редактор: д.ф.-м.н., профессор Глущенко А.Г. Рецензент: к.ф.-м.н., доцент Рычков В.А.
Самара 2008
2
ВНИМАНИЕ! Подключение лабораторной установки к сети обязательно должно проводиться в присутствии лаборанта или преподавателя!
ЛАБОРАТОРНАЯ РАБОТА № 67
Определение отношения удельных теплоемкостей газа методом адиабатического расширения
ЦЕЛЬ РАБОТЫ
Определение отношения удельных теплоемкостей газа методом адиабатического расширения.
ПРИБОРЫ И МАТЕРИАЛЫ
Стеклянный сосуд с краном, водяной манометр, ручной насос.
ЛИТЕРАТУРА
1.Сивухин Д.В. Общий курс физики. т.II. Молекулярная физика и термодинамика - М: Физматлит, МФТИ, 2002.
2.Савельев И.В. Курс общей физики. т.I. – М.: Астрель, 2003.
3.Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высш.шк., 2000.
4.Трофимова Т.И. Курс физики. – М.: Высшая школа, 2001.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Какой газ называется идеальным? (Смотри приложение № 1)
2.Какими параметрами характеризуется состояние газа? Дайте мо- лекулярно-кинетическое толкование параметров р,Т.
3.Запишите формулу, связывающую температуры по шкале Кельвина и по шкале Цельсия? Каков физический смысл абсолютного нуля?
4.Запишите уравнение состояния идеального газа.
5.Какой процесс называется изотермическим? Запишите и сформулируйте закон Бойля-Мариотта и начертите график зависимости давления от объема.
6.Какой процесс называется изохорическим? Запишите и сформулируйте закон Шарля. Начертите график зависимости давления от температуры.
7.Какой процесс называется изобарическим? Запишите и сформулируйте закон Гей-Люссака. Начертите график зависимости объема от температуры.
8.Какой процесс называется адиабатическим? Запишите уравнение Пуассона и представьте его графически. (см. приложение № 2)
9.Запишите и сформулируйте первый закон термодинамики. Дайте понятие внутренней энергии, работы, количества тепла.
10.Запишите выражение для работы расширения газа. Как ее представить графически на рV диаграмме.
11.Примените первый закон термодинамики ко всем процессам, рассматриваемым в данной лабораторной работе и проанализируйте вытекающие из него следствия.
12.Дайте определение удельной и молярной теплоемкостей и запишите соотношение между ними.
13.Выведите уравнение Майера. Какая из теплоемкостей Ср или CV больше и почему?
14.Что понимают под числом степеней свободы? Запишите связь между γ и числом степеней свободы i.
15.Зная число степеней свободы молекул воздуха, рассчитайте γ и сравните со значением γ, полученным опытным путем.
16.Нарисуйте и поясните на рV диаграмме последовательно все процессы, происходящие с газом.
17.Какова причина изменения температуры воздуха в баллоне при накачивании воздуха в баллон и при выпуске его из баллона?
18.Выведите расчетную формулу для определения отношения теплоемкостей γ.
19.Расскажите порядок выполнения работы.
3 |
4 |
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ
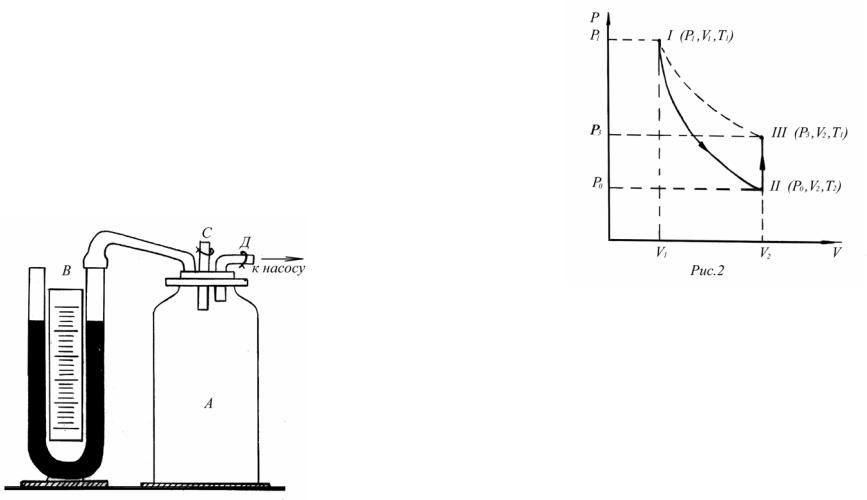
Экспериментальная установка состоит из стеклянного баллона А, соединенного с манометром В и насосом (рис.1).
Если при помощи насоса накачать в баллон некоторое количество воздуха, то давление и температура воздуха внутри баллона будут выше давления и температуры окружающей среды. Повышение температуры происходит вследствие увеличения внутренней энергии газа за счет совершаемой при накачке газа работы внешних сил.
Между баллоном и окружающей средой будет происходить процесс теплообмена, и через некоторое время температура воздуха в баллоне станет равной температуре окружающей среды Т1.
Этому тепловому равновесию будет соответствовать установившаяся разность уровней в манометре Н. Давление воздуха будет
p1 = p0+ρg Н,
где: p0 - атмосферное давление;
ρ – плотность жидкости в манометре
Рис.1.
5
Будем рассматривать не весь объем воздуха в баллоне, а удельный объем, т.е. объем единицы массы газа. Обозначим удельный объем через V1. Таким образом, состояние воздуха внутри баллона, которое назовем Ị состояние, характеризуется параметрами p1, V1, T1. Отметим это состояние на графике (рис.2).
Если открыть на которое время кран С, то воздух в баллоне будет расширяться. Этот процесс расширения, происходящий достаточно быстро, можно считать адиабатическим, т.к. не произошло значительного теплообмена с окружающей средой. Работа расширения газа была произведена за счет внутренней энергии газа, что привело к ее уменьшению, вследствие чего температура газа в баллоне понизилась Т2 < Т1.
Давление воздуха в баллоне понизится до атмосферного р2 = р0, а удельный объем газа увеличится V2 > V1. В результате адиабатического процесса система приходит в состояние 2 с параметрами р0, V2, T2. На графике (рис.2) точки I и II соединены кривой – адиабатой.
Для адиабатического процесса имеет место уравнение Пуассона, поэтому для состояний I и II можно записать:
|
|
|
pV γ |
= const , |
|
|
|||
|
|
|
p V γ |
= p V γ , |
|
|
|||
|
|
|
1 |
1 |
|
2 |
2 |
|
|
|
γ |
p2 |
|
|
p0 |
|
|
||
|
V1 |
|
= |
= |
|
. |
(1) |
||
|
p1 |
p0 |
+ ρgh |
||||||
V2 |
|
|
|
|
|||||
6

Охладившийся при расширении воздух в баллоне через некоторое время вследствие теплообмена нагреется до температуры Т3, равной температуре внешней среды, т.е. Т3 = Т1. Давление возрастает до некоторой величины
р3 = р0 + ρgh,
где h – показание манометра в новом состоянии, которое обозначим состояние III.
Удельный объем воздуха не изменится, V3 = V2. Таким образом, состояние III будет характеризоваться параметрами Р3, V2, T1.
Процесс перехода системы из состояния II в состояние III является изохорическим процессом.
В состояниях I и III воздух имеет одну и ту же температуру. Кривая, соединяющая точки I и III на графике, является изотермой, следовательно, для этих состояний можно применить закон Бойля-Мариотта: pV = const ,
|
|
|
|
p1V1 = p3V2 , |
|
|
|
|||||
V1 |
= |
|
p3 |
= |
p0 + ρgh |
|
, |
|
||||
V |
|
p |
p + ρgH |
|
|
|||||||
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
γ |
|
|
p0 + ρgh |
|
γ |
|
||||
|
V1 |
|
= |
|
|
. |
(2) |
|||||
|
|
p0 + ρgH |
||||||||||
V2 |
|
|
|
|
||||||||
Приравнивая выражение (1) и (2), получим:
p0 |
|
p0 + ρgh |
γ |
|
= |
. |
|||
p0 + ρgH |
|
|||
p0 + ρgH |
||||
Прологарифмируем полученное выражение и найдем γ:
γ = |
lg( p0 + ρgH ) −lg p0 |
||
|
. |
||
lg( p + ρgH ) −lg( p + ρgh) |
|||
0 |
0 |
|
|
Так как давления p0 , p0 + ρgH , |
p0 + ρgh мало отличаются друг от |
||
друга, то разности логарифмов можно принять пропорциональными разностям самих давлений и приближенно положить
γ = |
|
( p0 + ρgH ) − p0 |
|
= |
ρgH |
, |
|
( p |
+ ρgH ) −( p |
+ ρgh) |
ρg(H −h) |
||||
0 |
0 |
|
|
|
|
|
|
|
|
γ = |
H |
. |
|
|
(3) |
|
|
H −h |
|
|
|||
|
|
|
|
|
|
|
|
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Убедившись в том, что кран С (рис.1) закрыт, открывают кран Д
иосторожно, с помощью насоса, нагнетают воздух в баллон до возможно большей разности уровней в манометре.
2.Закрывают кран Д и, выждав, пока уровни жидкости в манометре не перестанут изменяться, записывают разность уровней Н (отсчет удобнее вести по нижнему краю мениска).
3.Быстро открывают кран С и сразу, как только уровни в манометре сравниваются, его закрывают. Когда давление окончательно установится, производят второй отсчет разности уровней в манометре h. Опыт повторяют 7 раз.
4.Подставляя в формулу γ = HH−h значения H и h , взятые из каж-
дого отдельного опыта, вычисляют γ1, γ2, γ3, ... .
5.Определив среднее значение <γ>, вычисляют абсолютные ошиб-
ки каждого измерения, среднюю квадратичную ошибку S<γ> и доверительный интервал, как для прямых измерений.
6.Все полученные опытом и вычислением результаты измерений заносят в таблицу № 1.
|
Таблица № 1. |
|
|
|
|
|
|
|
||
№, |
|
Н, |
h, |
γi |
<γ> |
∆γi |
(∆γi)2 |
S<γ> |
∆γ |
<γ> ± ∆γ |
п/п |
|
мм |
мм |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
8 |
ЛАБОРАТОРНАЯ РАБОТА № 70
Определение коэффициента вязкости жидкости.
ЦЕЛЬ РАБОТЫ
Определить коэффициент вязкости жидкости методом Стокса.
ПРИБОРЫ И МАТЕРИАЛЫ
Цилиндрическая стеклянная трубка, заполненная глицерином, стальные шарики, электрический секундомер, микрометр.
ЛИТЕРАТУРА
1.Сивухин Д.В. Общий курс физики. т.II. Молекулярная физика и термодинамика - М: Физматлит, МФТИ, 2002.
2.Савельев И.В. Курс общей физики. т.I. – М.: Астрель, 2003.
3.Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высш.шк., 2000.
4.Трофимова Т.И. Курс физики. – М.: Высшая школа, 2001.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Объясните происхождение сил внутреннего трения между слоями движущейся жидкости с точки зрения молекулярно-кинетической теории. (Смотри приложение № 3)
2.Выведите выражение для силы внутреннего трения на основании молекулярно-кинетической теории.
3.Запишите закон Ньютон для сил внутреннего трения.
4.Что называется градиентом скорости?
5.Каков физический смысл коэффициента вязкости?
6.Дайте определение единицы измерения коэффициента вязкости в системе СИ.
7.Запишите закон Стокса, при каких условиях он выполняется.
8.Выведите расчетную формулу для определения коэффициента вязкости.
9.Почему силы, действующие на шарик, который движется в вязкой среде, с некоторого момента уравновешиваются?
10.Изобразите графически характер изменения скорости со временем при падении тела в вязкой среде. Поясните его.
11.Расскажите порядок выполнения работы.
9
МЕТОД СТОКСА И ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Рассмотрим свободное падение тела внутри вязкой жидкости. При движении в вязкой среде тело испытывает сопротивление. При малых скоростях υ ≤1 м/ с , когда не возникает вихрей, сила сопротивления обусловлена вязкостью жидкости.
Слой жидкости, непосредственно прилегающий к твердому телу, прилипает к его поверхности и увлекается им полностью. Следующий слой увлекается за телом с меньшей скоростью. Таким образом, между слоями возникают силы трения. В этом случае сила сопротивления по закону, установленному Стоксом, прямо пропорциональна первой степени скорости движения тела, коэффициенту вязкости и линейным размерам тела.
Для шаров, движущихся в вязкой жидкости, по закону Стокса сила сопротивления
Fc = 3πdηυ ,
где: d - диаметр шара;
η - коэффициент вязкости;
υ - скорость установившегося движения шарика. Кроме этой силы, на шар действует сила тяжести
P = mg = ρVg = π6d 3 ρg ,
где ρ - плотность материала шарика;
V = |
4 |
πR |
3 |
|
4 |
d |
3 |
πd 3 |
- объем шарика; |
||
|
|
= |
|
π |
|
|
= |
|
|||
3 |
|
3 |
2 |
6 |
|||||||
|
|
|
|
|
|
|
|
||||
d - диаметр шарика;
g- ускорение свободного падения;
ивыталкивающая сила Архимеда
FA = ρ1Vg = π6d3 ρ1 g ,
где ρ1 - плотность жидкости.
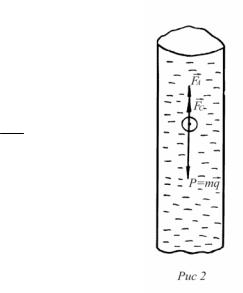
Направление этих сил дано на рис.2. Согласно 2-му закону Ньютонаur ur uur
ma = mg + F c + FA
или в скалярной форме
ma = mg −(Fc + FA ) .
10

Так как плотность шарика больше плотности жидкости, то в начале движения P > FA + Fc и шарик движется ускоренно. С увеличением
скорости растет сила Стокса Fc , наконец, наступает момент, когда
mg = FA + Fc .
после чего шар движется равномерно, т.е. с постоянной скоростью. Подставим выражения для сил в полученное равенство и преобразу-
ем его, тогда получим
|
|
|
ρVg = ρ1Vg +3πdηυ , |
|
|
|
||||
|
ρVg − ρVg |
|
(ρ − ρ )Vg |
|
(ρ − ρ ) |
πd 3 |
|
(ρ − ρ )d 2 g |
|
|
η = |
1 |
= |
1 |
|
= |
1 |
|
g = |
1 |
, |
3πdυ |
3πdυ |
|
3πdυ |
6 |
18υ |
|||||
|
|
|
|
|
|
|||||
|
η = |
(ρ − ρ )d 2 g |
. |
|
(1). |
|
|
|
||
|
|
1 |
|
|
|
|
||||
|
|
18υ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Измерив диаметр шара и определив опытным путем скорость его движения, по формуле (1) можно определить коэффициент вязкости жидкости. Для определения скорости используется прибор Стокса, изображенный на рис.3.
Цилиндрическая трубка наполнена испытуемой жидкостью (глицерином). В жидкости свободно падает шарик. Ускоренное движение шарика переходит в равномерное на глубине 5-8 см. На этой глубине нанесена метка m. В момент прохождения шариком метки m включают секундомер и выключают его при прохождении шариком метки n. Измерив расстояние между метками, определяют скорость равномерного движения шара
υ = |
s |
. |
(2) |
|
|||
|
t |
|
|
Таким образом, коэффициент вязкости
η = |
(ρ − ρ )d 2 gt |
. |
(3) |
|
1 |
||||
18s |
||||
|
|
|
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Составляют таблицу результатов измерений (табл.1).
2.Измеряют расстояние s между метками m и n по шкале, укрепленной около трубки.
3.Берут шарик, измеряют его диаметр микрометром и заносят это значение в табл.1.
4.Бросая шарик в трубку с глицерином, включают электросекундомер в момент прохождения шариком метки m и выключают его в момент прохождения шариком метки n (момент прохождения меток отмечают, помещая глаз на уровне отметок m и n).
5.Определяют по секундомеру время движения t шарика между метками.
6.Измерения проводят не менее 7 раз (т.е. с семью шариками).
7.Вычисляют коэффициент внутреннего трения ηi для каждого из шаров по формуле (3).
8.Рассчитывают погрешность результатов измерений способом, применяемым для прямых измерений.
9.Результаты измерений и вычислений заносят в табл.1.
Таблица № 1.
№ |
ρ, |
ρ1, |
|
s, |
d, |
t, |
ηi, |
<η>, |
∆ηi, |
S<η>, |
∆η, |
<η> ± ∆η, |
|||
п/п |
кг |
кг |
|
м |
мм |
с |
Па·с |
Па·с |
Па·с |
Па·с |
Па·с |
Па·с |
|||
|
|
м3 |
|
|
м3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
12 |

ЛАБОРАТОРНАЯ РАБОТА № 71
Определение коэффициента теплопроводности металлов
ЦЕЛЬ РАБОТЫ
Определить коэффициент теплопроводности металлического стержня, нагреваемого с одного конца.
ПРИБОРЫ И МАТЕРИАЛЫ
Источник питания (ИП), макет установки, включающий печь, длинный цилиндрический стержень, термопары, милливольтметр ПП-6, амперметр, вольтметр.
ЛИТЕРАТУРА
1.Сивухин Д.В. Общий курс физики. т.II. Молекулярная физика и термодинамика - М: Физматлит, МФТИ, 2002.
2.Савельев И.В. Курс общей физики. т.I. – М.: Астрель, 2003.
3.Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высш.шк., 2000.
4.Трофимова Т.И. Курс физики. – М.: Высшая школа, 2001.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что представляет собой процесс теплопроводности? (см приложение № 3)
2.Запишите формулу для явления теплопроводности.
3.Дайте определение градиента температуры.
4.Каков физический смысл коэффициента теплопроводности?
5.Дайте определение единицы измерения коэффициента теплопроводности в системе СИ.
6.Запишите формулу количества тепла, необходимого для нагревания тела.
7.Напишите расчетную формулу для определения коэффициента теплопроводности.
8.Каким методом определяется тепло, получаемое стержнем в единицу времени от печи?
9.Напишите уравнение теплового баланса для отрезка стержня.
10.Расскажите порядок выполнения работы.
МЕТОД ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ
Если вдоль оси стержня (ось х) имеется градиент температуры, то в этом направлении через сечение, перпендикулярное оси, устанавливается поток тепла, величина которого определяется уравнением теплопроводности (закон Фурье)
q = −χ |
dT |
S , |
(1) |
|
dx |
||||
|
|
|
где: χ - коэффициент теплопроводности среды,
q – поток тепла через поперечное сечения стержня, dTdx - градиент температуры,
S – площадь поперечного сечения стержня.
Если нет причин, обуславливающих потоки тепла в поперечных y и z направлениях, то в стационарном режиме распределение температуры вдоль стержня будет нелинейным, а градиент температуры и поток постоянными.
Уравнение (1) для этого случая перепишется в виде
q = −χ |
∆T |
S . |
(2) |
|
∆x |
|
|
В работе определяется коэффициент теплопроводности путем исследования стационарного распределения температуры вдоль металлического стержня, нагреваемого с одного конца. Поток тепла, обусловленный теплопроводностью металла, распространяется вдоль стержня.
Из-за того, что температура стержня выше температуры воздушной среды, даже при хорошей теплоизоляции стержня имеется некоторый тепловой поток через боковую поверхность, для учета которого вводят коэффициент теплоотдачи стержень-воздух α (в нашем случае α учитывает наличие теплоизоляции стержня). В этом случае распределение температуры Т вдоль стержня не является линейным, и описывается уравнением (4).
Через боковую поверхность элемента стержня длины dх в единицу времени теряется количество тепла
dq =α(T −T0 ) pdx ,
где: α - коэффициент теплоотдачи стержень-воздух, T – температура стержня,
T0 - температура окружающей воздушной среды, р - периметр поперечного сечения стержня
13 |
14 |

Через сечение с координатой x, тепловой поток определяется формулой Фурье
q(x) = −χ |
dT |
S . |
|
||
dx |
x |
|
Для сечения с координатой x + ∆х соответствующий поток
dT |
|
||
q(x + dx) = −χ |
|
|
S . |
|
|||
|
dx x+dx |
|
|
Запишем уравнение теплового баланса для элемента стержня dх
|
|
|
|
|
|
q(x) −q(x +dx) = dq , |
|
|
|
|
||||||||||
dT |
|
|
dT |
|
|
|
|
|
|
|
|
|
|
|||||||
−χ |
|
|
|
|
S + χ |
|
|
|
|
S =α(T −T0 ) pdx , |
|
|||||||||
|
|
|
|
|
|
|||||||||||||||
dx x |
|
dx |
x+dx |
|
|
|
|
|
|
|
||||||||||
dT |
|
|
dT |
|
|
|
|
|
|
|
|
|
||||||||
χ |
|
|
|
|
|
− |
|
|
|
S =α(T −T0 ) pdx . |
|
|
||||||||
dx |
|
|
|
|
||||||||||||||||
|
x+dx |
dx |
x |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
dT |
dT |
|
d 2T |
dx , и |
|||||||
Обратим внимание на то что |
|
|
|
− |
|
|
= |
|
|
|||||||||||
|
|
|
dx |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx x+dx |
|
dx x |
|
|
|
|||||
χd 2T dxS =α(T −T0 ) pdx , dx2
|
d 2T |
|
= α p |
(T −T ) . |
|
||
|
dx2 |
|
|||||
|
|
χS |
0 |
|
|||
Обозначим и получим |
|
= α p |
|
||||
|
|
a2 |
(3) |
||||
|
|
|
|
|
χS |
|
|
|
|
d 2T |
|
= a2 (T −T ) , |
(4) |
||
|
|
dx2 |
|
||||
|
|
|
|
0 |
|
||
где: T – температура стержня,
T0 - температура окружающей воздушной среды,
р и s – периметр и площадь поперечного сечения стержня, α, χ - коэффициенты теплоотдачи и теплопроводности.
Уравнение (4) является линейным уравнением второго порядка. Общее решение уравнения (4) имеет вид
T −T0 = Aeax + Be−ax .
Для определения постоянных А и В используем граничные условия. При x → ∞ , T →T0 , следовательно, А = 0.
При х = 0, T =T1 (Т1 - температура печи), отсюда B =T1 −T0 .
Подставляя значения А и В в общее решение, находим распределение температур вдоль стержня
T −T0 = (T1 −T0 )e−ax .
Зная температуру T точки x, можно найти величину a
a = |
1 |
ln |
T1 −T0 |
. |
(5) |
|
|
||||
|
x T −T |
|
|||
|
0 |
|
|
||
Согласно (3) а является комбинацией коэффициентов теплопроводности и теплоотдачи, поэтому для практических применений последней формулы надо ввести еще одну измеряемую величину, связанную только с коэффициентом.
Через элемент поверхности длиной dx теряется в единицу времени
dq =α(T −T ) pdx =α(T −T )e−ax pdx |
|
|||||||||||||
0 |
|
|
|
|
1 |
0 |
|
|
|
|
||||
Интегрируя это выражение от 0 до ∞, найдем |
|
|||||||||||||
∞ |
|
|
∞ |
|
|
|
|
|
|
α p(T −T ) ∞ |
||||
q = ∫α(T1 −T0 )e−ax pdx =α p(T1 −T0 )∫e−ax dx = − |
|
|
1 0 |
∫e−ax d(−ax) = |
||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
a |
0 |
= −α p(T1 −T0 ) (0 −1) = |
|
α p (T −T ) , |
|
|||||||||||
a |
|
|
|
|
|
a |
|
1 |
0 |
|
||||
|
|
|
|
|
|
|
|
|
||||||
α = |
|
|
qa |
. |
|
|
|
|
|
|
(6) |
|||
p(T |
−T ) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
Подставляя (6) в (3) получим |
|
|
|
|
|
|
|
|
|
|
|
|||
a2 = α p |
= |
|
qa |
|
|
|
|
p |
|
, |
|
|||
p(T −T ) χS |
|
|||||||||||||
χS |
|
|
|
|
||||||||||
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
χ = q |
|
|
1 |
|
|
. |
|
|
|
|
||||
aS(T −T ) |
|
|
|
|
||||||||||
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
Подставляя выражение для а из (5), получим |
|
|||||||||||||
χ = |
|
|
|
|
qx |
|
|
|
|
|
|
|
. |
(7) |
S(T −T ) ln |
T |
−T |
|
|||||||||||
|
|
1 |
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
0 |
|
T −T0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
В реальных условиях имеется стержень конечной длины l, поэтому выражение (6) для потока тепла через боковую поверхность стержня найдено с ошибкой.
Проинтегрируем выражение для dq по x от l до ∞, тогда величина, которой мы пренебрегли при расчете q, получится равной δq
δq = αap (T1 −T0 )e−al
15 |
16 |

Найдем относительную погрешность формулы (6)
δq |
= e−al . |
(8) |
|
q |
|||
|
|
Чем больше длина стержня тем точнее формула (6).
Для расчета коэффициента теплопроводности по формуле (7) нужно знать поток тепла q, теряемый стержнем через боковую поверхность. В стационарном режиме этот поток равен теплу, получаемому от печи в единицу времени, т.е. потоку, который проходит через сечение с координатой x = 0. Кроме того, нужно знать температуру Т какой-либо точки стержня на расстоянии x от нагреваемого торца, площадь поперечного сечения стержня S, температуры печи Т1 и воздушной среды Т0.
Для определения тепла, получаемого стержнем в единицу времени от печи, используется следующий метод. Тепло Q, генерируемое печью, частично идет на создание теплового потока q, частично – в окружающее печь пространство q1.
Q = q + q1 ,
откуда
q = Q −q1 . |
(9) |
Если нагреватель печи питается током I3 при напряжении U3, то
Q = I3U3 .
Пусть температура печи, измеренная термопарой есть n2 (в милливольтах). Удалим стержень из печи; температура печи повысится и станет равной n3. Регулируя нагрев печи, понизим температуру в ней до прежнего значения n2. Если I2 и U2 - новые величины тока и напряжения нагревателя, то тепло q1, теряемое печью в единицу времени равно
q1 = I2U2 .
Из (9) находим
q = I3U3 − I2U2 . |
(10) |
Для случая хорошей теплоизоляции стержня, q есть поток тепла через сечение стержня S в установившемся режиме.
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Схема установки приведена на рис.1.
Рис.1.
Напряжение от источника питания ИП подается к печи П. Амперметр А и вольтметр V позволяют измерить ток и напряжение нагревателя печи. Термопары (на схеме обозначены цифрами 1,2,3,4,5) служат для измерения температуры. Каждая термопара состоит из двух проводников (хромель-копель), спаянных в двух местах. Один спай находится в контакте с печью или стержнем, другой опущен в сосуд с маслом, температура которого измеряется термометром. На рис.1 для простоты указана термопара 1. Термопары подключаются с помощью переключателя к милливольтметру ПП-63, который измеряет термоэдс, пропорциональную разности температур спаев. Пользуясь градуировочным графиком, по величине термоэдс находят температуру горячего спая.
17 |
18 |
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Записать в таблицу № 1 температуру окружающего воздуха Т0, а также координаты всех термопар вдоль стержня х2, х3, х4, х5.
2.Включить печь, установив ток, указанный на лабораторном столе. Дождаться стационарного режима.
3.Записать в таблицу величину теплового потока q , указанную на лабораторном столе.
4.Записать показание термопары печи n1.
5.Переключателем подключить поочередно каждую термопару к потенциометру ПП-63; занести в таблицу показания всех термопар.
6.Пользуясь градуировочным графиком, найти температуру Ti для каждой координаты xi, а также температуру T1 печи, соответствующую показанию n1.
7.Построить график T = f (x) .
8.Рассчитать χ по формуле (7), найти его среднее значение <χ>.
9.Найти погрешность ∆χ методом прямых измерений.
10.Заполнить таблицу № 1.
Таблица № 1
№, |
Т0, |
q, |
n1, |
Т1, |
х, |
n, |
Т, |
χi, |
<χ>, |
∆χ, |
п/п |
оС |
Вт |
мВ |
оС |
см |
мВ |
оС |
Вт . |
Вт . |
Вт . |
|
|
|
|
|
|
|
|
м·К |
м·К |
м·К |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 78
Изменение энтропии при фазовом переходе первого рода
ЦЕЛЬ РАБОТА
Определить температуру плавления и кристаллизации олова. Вычислить изменение энтропии при этих процессах.
ПРИБОРЫ И МАТЕРИАЛЫ
Электроплитка, тигель с оловом, термопара, потенциометр.
ЛИТЕРАТУРА
1.Сивухин Д.В. Общий курс физики. т.II. Молекулярная физика и термодинамика - М: Физматлит, МФТИ, 2002.
2.Савельев И.В. Курс общей физики. т.I. – М.: Астрель, 2003.
3.Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высш.шк., 2000.
4.Трофимова Т.И. Курс физики. – М.: Высшая школа, 2001.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что понимают в термодинамике под фазой? Приведите примеры различных фаз.
2.Дайте определение фазового перехода первого рода. Приведите примеры.
3.Дайте определение фазового перехода второго рода. Приведите примеры.
4.Дайте определение процессов плавления и кристаллизации.
5.Объясните процесс плавления на основании молекулярнокинетической теории строения вещества.
6.В чем отличие процессов плавления кристаллических и аморфных тел? Сравните их кривые нагревания.
7.Дайте определение удельной теплоты плавления.
8.Запишите формулу теплоты плавления.
9.Объясните процесс кристаллизации с точки зрения молекулярнокинетической теории строения вещества.
10.Дайте определение статистического веса и энтропии.
11.Какова связь между энтропией и статистическим весом?
19 |
20 |
