0232690

При экспериментальном определении молярной массы эквивалентов на основе опытных данных используют закон эквивалентов: все вещества реагируют между собой в эквивалентных количествах. Допустим, установлено: 3.24 г металла образуют 3.48 г оксида. Очевидно, 3.48 г оксида содержат 3.48–3.24 = 0.24 г кислорода. Рассчитаем число молей эквивалентов кислорода

(в соответствии с законом эквивалентов) такое же число молей эквивалентов металла, поэтому молярную массу эквивалента металла можем определить как

Эквивалентный объем (Vf) – это объем, который занимает 1 моль эквивалентов данного вещества, находящегося в газообразном состоянии при нормальных условиях. Так как 1 моль газообразного вещества занимает объем

22.4 л, то очевидно Vf = f · 22.4, например, Vf(О2) = 0.25 · 22.4 = 5.6 л. Знание эквивалентного объема позволяет определять молярную массу эквивалентов в тех случаях, когда в реакции участвуют газообразные вещества. Так, если установлено, что на восстановление 1.8 г оксида металла требуется 833 мл водорода, взятого при нормальных условиях, то, зная эквивалентный объем водорода (Vf(Н2) = 0.5 · 22.4 = 11.2 л), легко найти число молей эквивалентов водорода, а следовательно и оксида металла, вступивших в реакцию:

Молярная масса эквивалента оксида металла будет равна:

1.1.7. Способы выражения состава раствора

Раствором в химии называют равновесную гомогенную фазу, состав которой можно изменять плавно (не скачками) без нарушения ее однородности. Состав чаще выражают через концентрации или доли.

Если имеем отношение массы, объема или количества какого-либо компонента соответственно к массе, объему или количеству всех веществ раствора, то это массовая ( – читается «омега»), объемная ( – «фи») или моляр-

ная ( – «хи») доли данного компонента. Их выражают десятичной дробью или

в процентах.

Для характеристики состава жидких растворов обычно указывают его концентрацию (что на латинском языке означает «сгущение»). Она чаще вы-

10

ражается отношением количества растворенного вещества к объему всего раствора (V) или к массе растворителя (mр ля ) (табл. 1):

где n – количество вещества, nf – количество вещества эквивалентов, m- масса вещества, раствора или растворителя.

2. ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ И КИНЕТИКИ

2.1. ТЕРМОХИМИЯ. ЭНТРОПИЯ. ЭНЕРГИЯ ГИББСА

Химическая термодинамика – это раздел химии, в котором изучается энергетика химических процессов и определяется направление их протекания.

Для удобства изучения необходимо изолировать объекты исследования от окружающей среды. Завершенная совокупность тел, выделенная из среды, называется системой; а химическая система – это все частицы, вступающие в реакцию, и продукты их взаимодействия.

Если между системой и окружающей средой может осуществляться и мас- со-, и теплообмен, то система называется открытой; если возможен лишь теплообмен, то – закрытой; если же нет ни массо-, ни теплообмена, то система

изолированная.

В изолированной системе энергия (Е) не создается и не исчезает, лишь переходит из одной формы в другую, так что сумма энергий всех ее форм остается постоянной. Это закон сохранения энергии, или первое начало термо-

динамики.

11

2.1.1. Термохимия

Химические процессы могут протекать с выделением или поглощением различных видов энергий: электрической, световой и т.п., но чаще сопровождаются тепловыми эффектами1, которые изучают в особом разделе – термо-

химии.

В рамках термохимии 1-ое начало термодинамики: тепловой эффект реакции (Q) складывается из изменения внутренней энергии данной системы ( U ) и работы (A), совершенной этой системой (в частности, работы расширения), т. е.:

Внутренняя энергия (U) – это вся энергия системы без учета ее кинетической и потенциальной энергии как макротела, поэтому U – функция состояния системы.

Состояние системы определяется параметрами: T, p, V и x, где x – качественный и количественный состав системы. Причем изменение хотя бы одного параметра называется процессом, а изменение x – химической реак-

цией.

Если какая-либо характеристика вещества является функцией состояния, то ее величина определяется только значениями параметров в данный момент и не зависит от пути, каким система пришла в данное состояние. И если известны значения функции в «исходной» точке процесса и в «конечной», то изменение функции при переходе системы из 1-ой точки во 2-ую равно разности ее значений в этих точках. Поэтому в формуле (1) изменение внутренней энергии записано как U .

Напротив, величина A (если это работа расширения) определяется формулой:

V2

A p dV ,

V1

поэтому А – функция пути процесса2, а не состояния системы. Следовательно,

иQ в соответствии с равенством (1) – функция пути.

Визобарном режиме: p = const и A p V , т. е. работа, следовательно,

иQ (в соответствии с формулой (1) становятся функциями состояния). В этом случае Q обозначается как H (где H U pV и называется энтальпией, что в

переводе с греческого, означает теплосодержание расширенной (до объема V) системы).

Итак, H (изменение энтальпии) является функцией состояния.

1И другие виды энергии в конечном итоге переходят в тепловую.

2Быть функцией пути процесса – это значит зависеть от этого пути, т. е. от того, каким образом изменяются параметры системы (T, p, V и x) при осуществлении процесса.

12

Таким образом, тепловой эффект химической реакции, протекающей при p const , (обозначается Hr ) 1 не зависит от пути процесса, а определяет-

ся лишь начальным и конечным состоянием системы. Это формулировка закона Гесса, из которого вытекают два следствия:

С л е д с т в и е 1. В стандартных условиях (ст.у.): p 101325 Па 2,

T = 298 К (или 25 0С), – тепловой эффект получения одного моля данного соединения из исходных простых веществ есть величина постоянная, называет-

ся стандартной теплотой образования (обозначается H0f ,298 ) 3 и приводит-

ся в справочниках. Очевидно, что H0f ,298 простого вещества из этого же просто-

го вещества в ст.у. равна 0.

С л е д с т в и е 2. Тепловой эффект реакции при данной температуре равен сумме теплот образования продуктов реакции (п.р.) за вычетом суммы теплот образования исходных веществ, т.е. реагентов (р.) (если все указанныеHf определены при одной и той же данной T). Для ст.у. это запишется сле-

дующим образом:

∆Hr,2980 i H0f,298 (п.р.) j H0f,298 (р.).

Причем знак включает суммирование и по числу молей каждого соединения с учетом стехиометрии уравнения реакции. Например, для процесса:

4NH3 3O2 2N2 6H2O имеем: ∆Hr,2980 6∆∆0f,298 (H2O) 4∆∆0f,298 (NH3 ).

Закон Гесса позволяет по справочным данным рассчитать тепловой эффект любого процесса, даже если он не осуществим экспериментально, используя схемы циклов. Например, чтобы рассчитать энтальпию образования ( ∆Hх )

кристаллогидрата ( CuSO4 5H2O (медного купороса)) из безводного (б/в) сульфата меди, составляем следующий цикл:

где ∆H1 и ∆H2 – энтальпия растворения в воде безводной соли и кристаллогидрата соответственно (их значения есть в справочнике).

По закону Гесса: H1 Hx H2 . Откуда ∆Hх ∆H1 ∆H2 .

1Буква r – начальная в англ. слове «reaction», что значит «реакция».

2В химии часто используется единица давления – атмосфера, и стандартное условие по давлению – это р=1 атм. (или 760 мм ртутного столба).

3Буква f – начальная в англ. слове «formation», что значит «образование».

13

Вместо цикла можно использовать термохимические уравнения для отдельных стадий цикла. Чтобы уравнение являлось термохимическим, оно должно: содержать указания агрегатных состояний всех соединений и включать значение теплового эффекта процесса, причем реакция считается эндотермической, т.е. идет с поглощением тепла системой, если H 0 , и экзотермической (тепло выделяется) – при H 0 .

П р и м е р. Определить экспериментально тепловой эффект превращения графита в алмаз невозможно. Но используя термохимические уравнения, этот эффект можно рассчитать, производя обыкновенные алгебраические действия. Известно, что и графит, и алмаз сгорают в атмосфере кислорода с образованием одного и того же продукта (углекислого газа), но с выделением

Если вычесть из первого термохимического уравнения второе, то получим:

т. е. с позиции термодинамики графит должен переходить в алмаз с поглощением небольшого количества тепла. Однако известно, как трудно это осуществить.

2.1.2. Энтропия. Энергия Гиббса

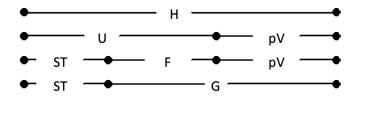
Связь между различными термодинамическими величинами, характеризующими данное вещество при постоянном давлении, можно изобразить графически в виде соотнесенных отрезков:

'

где F – химическая энергия, pV – механическая работа (совершенная для придания данной системе при данном давлении данного объема), G – свободная энергия системы (называется энергией Гиббса), а ST – связанная энергия, ибо ее нельзя перевести в работу (в отличие от свободной) без изменения Т, т. к. это энергия теплового движения.

Связанная энергия растет с повышением температуры, поскольку ST – это произведение коэффициента S на температуру. Но и сам коэффициент S,

14

называемый энтропией1, тоже растет при увеличении T, ибо является ме-

рой беспорядка в веществе: чем менее упорядочено соединение (в частности, чем интенсивнее тепловое движение в нем), тем больше значение S.

Энтропия идеального кристалла при абсолютном нуле ( S0 ) равна ну-

лю, а с повышением температуры S растет. Причем особенно значительно она увеличивается при плавлении вещества и еще более – при переходе его в газообразное состояние, когда в нем резко возрастает беспорядок.

При данной Т энтропия одного моля данного соединения будет тем больше, чем больше в нем число частиц, чем они разнороднее, чем сложнее сами частицы и чем больше их молекулярная масса. Кроме того, величина S тем выше, чем больший объем занимает 1 моль вещества. А изменение энтропии в ходе реакции будет тем значительнее, чем сильнее различаются реагенты и продукты данной реакции по указанным параметрам.

Для большинства веществ рассчитали стандартные2 значения энтропии ( S0298 ) и поместили в справочники [1]. А поскольку S, как и H , – функция со-

стояния, то ее изменение в ходе химического процесса ( Sr0,298 ) находят по аналогичной формуле:

∆Sr,2980 iS0298 (п.р.) jS0298 (р.).

Например, для реакции: 4NH3 3O2 2N2 6H2 O ,

имеем: Sr0,298 2S0298 (N2 ) 6S0298 (H2 O) 4S0298 (NH3 ) 3S0298 (O2 ) .

2.1.3.Формула Гиббса. Разрешенность процессов

спозиции термодинамики

Из графика (в виде соотнесенных отрезков), приведенного выше, видно, что G H ST , следовательно, G – тоже функция состояния (при p const ),

поэтому изменение свободной энергии в ходе реакции можно рассчитать по формуле (она называется формулой Гиббса):

Причем, если изменение G положительно ( G 0 ), то это означает, что свободная энергия системы при взаимодействии веществ должна самопроизвольно возрастать, что невозможно, поэтому такой процесс запрещен. Если же изменение G отрицательно ( G 0 ), т. е. энергия Гиббса в ходе реакции уменьшается, то процесс должен идти самопроизвольно.

Рассмотрим взаимодействия в системах, в которых начальные условия

стандартные: Т = 298 К, р =1 атм. и, кроме того, т.н. эффективные кон-

1От греческого «эн» – в и «тропе» – превращение.

2Стандартные значения S рассчитаны для одного моля каждого соединения, находящегося в наиболее устойчивом его состоянии, при p = 1 атм. и T = 298 К.

15

центрации каждой из реагирующих частиц равны по 1моль/л. (Имеются в виду частицы (молекулы, ионы и т.п.) не только исходных веществ, но и продуктов взаимодействия.)

Эффективная концентрация иначе называется активностью 1 (обозначается буквой а). Она равна произведению коэффициента активности (f) на истинную концентрацию частиц данного сорта (C): a=f·C.

Коэффициент активности показывает долю сравнительно свободных (активных) частиц, не участвующих в «постороннем» межчастичном взаимодействии (ибо оно не приводит к осуществлению данной реакции, поэтому «отвлекает» от нее). Так, для процесса: А + В = С, «посторонней» является ассоциация частиц А и B не между собой, а с C или со стенками сосуда и т. п.

Подчеркнем, что стандартные значения активностей частиц (ai=1 моль/л) могут соблюдаться лишь в первый момент реакции. А далее, если процесс идет, например, вправо, активности частиц реагентов снижаются, а продуктов – растут.

Для стандартных условий формула Гиббса запишется следующим образом:

процесс должен идти самопроизвольно, а при Gr0,298 0 реакция запрещена.

Формула (3а) позволяет оценить термодинамическую разрешенность процесса при любой (не только стандартной) температуре, используя Hr0,298 и

Sr0,298 (см. разделы 2.1.1 и 2.1.2), поскольку значения Hr0 и Sr0 мало зависят

Используя формулу (3б), проведем оценку знака G0 , а значит, термодинамическую разрешенность химического взаимодействия в зависимости от тем-

1 Иногда вместо активностей газообразных веществ берут парциальные давления (их стандартные значения равны 101325 Па или 1 атм. по каждому газу данной системы).

16

ным нулю, тогда из формулы (3б) получим: T H0 / S0 .

С л у ч а й 4. Если H0 0 и S0 0 (реакция, обратная предыдущей), то возможны те же два варианта (рассмотрите их сами), но выводы обратные.

Изменение G в процессе можно посчитать по формулам, аналогичным формулам изменения энтальпии и энтропии, используя табличные значения

∆G0 :

∆Gr,2980 iG0298 (п.р.) jG0298 (р.).

2.2.КИНЕТИКА

2.2.1.Определение скорости реакции

Химическая кинетика – раздел химии, рассматривающий скорость

химических процессов и их механизм. Скорость теоретически определяется числом элементарных актов взаимодействия1 в единицу времени в едини-

це объема (в гомогенных системах) или на единице поверхности (для гетерогенных реакций).

На практике независимо от того гомогенной или гетерогенной является система, скоростью процесса считают изменение концентрации какого-либо вещества в единицу времени в жидкой или газовой фазе.

2.2.2. Кинетическое уравнение

Зависимость скорости от различных факторов выражается т.н. кинетическим уравнением. Например, в случае процесса:

1 В случае многостадийного процесса имеется в виду лимитирующая его стадия.

17

если он является гомогенным и одностадийным1, кинетическое уравнение для

обратной реакций соответственно. Они отражают влияние природы реагентов3,

температуры и др. на скорость. Физический смысл k и k , как следует из кинетических уравнений, – это скорости процессов (прямого и обратного) при стандартных значениях активностей (равных, напоминаем, по 1 моль/л). Эти константы имеют размерность скорости, поскольку в кинетические уравнения активности подставляются в относительных единицах (по отношению к 1 моль/л), т. е. безразмерными.

Показатели степеней в кинетическом уравнении являются порядками процесса по соответствующим реагентам и отражают степень влияния активности каждой из взаимодействующих частиц на скорость. А сумма этих показателей называется общим порядком процесса. В случае гомогенной одностадийной реакции общий порядок совпадает с молекулярностью (т. е. с числом частиц, сталкивающихся при элементарном акте взаимодействия), значение которой не бывает более трех.

Отметим, что порядок реакции (в отличие от ее молекулярности) может быть дробным, что обычно указывает на многостадийность процесса. А также нулевым, например, для гетерогенной системы:

т.к. активности чистых твердых (а также жидких) веществ как постоянные

(при данной T) входят в константы, в нашем примере – в значение k . И в формулы вместо них подставляют 1.

2.2.3. Механизм химических реакций

Механизм большинства одностадийных химических взаимодействий, а также отдельных стадий многостадийных процессов, включает формирование т.н. активированного комплекса (а.к.) в качестве промежуточного продукта.

Активированный (или переходный4) комплекс – это такая ассоциа-

ция взаимодействующих (в элементарном акте реакции) частиц, при формировании которой происходит ослабление старых химических связей и зарожде-

1А также в случае лимитирующей стадии многостадийных реакций.

2Кинетическое уравнение можно записать через концентрации, но тогда оно не является стро-

18

ние новых (еще относительно слабых). Например, в случае одностадийного

трехмолекулярного процесса:

2NO Cl2 2NOCl ,

при столкновении двух частиц NO и одной Cl2 получается а.к. следующего вида:

O N Cl Cl N O ,

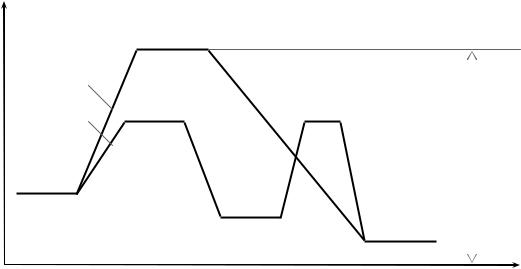
в котором затем рвется связь Cl Cl и упрочняются связи N Cl (пунктиром показаны ослабленные связи без уточнения их кратности). При осуществлении обратной реакции – наоборот, но а.к. тот же. Возможный механизм протекания одностадийного двухмолекулярного взаимодействия показан на рис. 1, линия (а).

Итак, для образования активированного комплекса частицы должны столкнуться при определенной ориентации относительно друг друга (в нашем примере молекулы NO - атомами азота с двух сторон частицы Cl2).

A2+B2

Ход реакции

Рис. 1. Изменение энергетического состояния реагирующих частиц в ходе экзотермического процесса (ослабленные связи изображены пунктиром, причем, чем длиннее пунктирный отрезок, тем слабее связь): (а) – в отсутствии катализатора; (б) – при наличии катализатора в системе

При этом, чтобы а.к. сформировался, сталкивающиеся молекулы должны обладать достаточно высокой энергией, т. е. соответствующей величине Ea.к. (рис. 1). Часто из-за слишком большого значения Ea.к. (практически не дос-

тигаемого частицами в условиях опыта) не идет даже термодинамически разрешенный процесс.

19