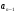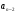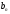- •2. Многочлены
- •1. Выполнить действия в алгебраической форме. Результат записать в алгебраической, тригонометрической и показательной формах.
- •2. Вычислить по формулам Муавра.
- •3. Выразить и через и , используя формулы Муавра и бином Ньютона.
- •4.Найти разложение по биному Ньютона
- •Выделить целую и дробную часть рациональной функции:
- •7. Разложить на линейные множители в с и неприводимые (линейные и квадратичные) множители в r. Сделать проверку.
2. Многочлены
Определение
2.1. Полиномом
(многочленом) относительно переменной
 называют выражение вида
называют выражение вида
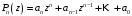 ,
,
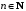 ,
,
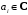 ,
где
,
где
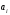 – коэффициенты
полинома;
– коэффициенты
полинома;
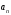 – старший
коэффициент, считается не равным нулю;
– старший
коэффициент, считается не равным нулю;
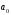 – свободный
член,
– свободный
член,
 – степень
полинома.
– степень
полинома.
Если
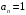 ,
то полином называется приведённым.
,
то полином называется приведённым.
При
делении многочлена
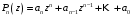 на
на
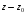 применяется метод сокращенного деления,
называемый схемой
Горнера.
применяется метод сокращенного деления,
называемый схемой
Горнера.
Схема Горнера
При
делении
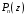 на
на
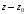 получается многочлен
получается многочлен
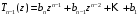 ,
а в остатке число
,
а в остатке число
 .
Тогда
.
Тогда
 =
=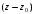
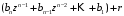 =
= .
.
|
|
|
|
|
… |
|
|
|
|
|
|
|
… |
|
|
Теорема
2.1. (Теорема
Безу).
Остаток от деления многочлена
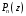 на
на
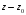 равен значению многочлена
равен значению многочлена
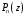 при
при
 .
.
Следствие
2.1. Если
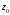 является корнем многочлена, то
является корнем многочлена, то
 делится на
делится на
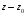 без остатка (нацело).
без остатка (нацело).
Определение
2.2. Уравнение
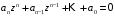 называется алгебраическим
уравнением
называется алгебраическим
уравнением
 -ой
степени.
-ой
степени.
Нахождение корней алгебраических уравнений.
1.
Алгебраическое уравнение нулевой
степени
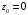 корней не имеет.
корней не имеет.
2.
Алгебраическое уравнение первой степени
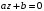 имеет один корень
имеет один корень
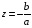 ,
,
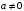 .
.
3. Корни
алгебраического уравнения второй
степени
 находятся по формулам:
находятся по формулам:
а)
 ,
,

б)
 ,
,
 ,
причём
,
причём
 и
и
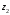 взаимно сопряженные числа.
взаимно сопряженные числа.
4. Корни
двучленного алгебраического уравнения
 -го
порядка
-го
порядка
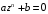 находят по формуле
находят по формуле
 .
.
Определение
2.3. Корень
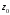 многочлена
многочлена
 называется корнем
кратности
называется корнем
кратности
 ,
если
,
если
 делится (без остатка) на
делится (без остатка) на
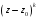 ,
но не делится на
,
но не делится на
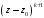 .
.
Если
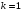 ,
то корень называется простым.
,
то корень называется простым.
Теорема
2.2. (теорема
Гаусса, основная теорема алгебры).
Уравнение
 ,
где
,
где
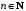 ,
,
 имеет
хотя бы один корень (в общем случае
комплексный).
имеет
хотя бы один корень (в общем случае
комплексный).
Следствие
2.1. Многочлен
степени
 с комплексными коэффициентами и со
старшим коэффициентом
с комплексными коэффициентами и со
старшим коэффициентом
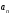 имеет ровно
имеет ровно
 корней и разлагается в произведение
корней и разлагается в произведение
 сомножителей вида
сомножителей вида
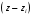 ,
т. е.
,
т. е.
 ,
и это представление единственно с
точностью до перестановки сомножителей.
,
и это представление единственно с
точностью до перестановки сомножителей.
Многочлены с действительными коэффициентами
Теорема
2.3. Если
комплексное число
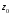 является корнем многочлена
является корнем многочлена
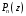 с действительными коэффициентами, то
сопряжённое число
с действительными коэффициентами, то
сопряжённое число
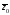 также является корнем этого многочлена
(доказать самостоятельно).
также является корнем этого многочлена
(доказать самостоятельно).
Следствие 2.4. Многочлен нечётной степени всегда имеет хотя бы один действительный корень.
Замечание 2.2. Среди приведенных многочленов с действительными коэффициентами неразложимыми на множители меньшей степени на множестве действительных чисел (неприводимыми многочленами) являются лишь многочлены первой степени и многочлены второй степени с отрицательным дискриминантом.
Теорема 2.5. Целые корни алгебраического уравнения с целыми коэффициентами являются делителями свободного члена.
Теорема
2.6. Для
того чтобы несократимая дробь

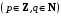 была корнем многочлена
была корнем многочлена
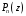 с целыми коэффициентами, необходимо,
чтобы
с целыми коэффициентами, необходимо,
чтобы
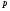 было делителем свободного члена
было делителем свободного члена
 ,
а число
,
а число
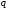 делителем
старшего коэффициента
делителем
старшего коэффициента
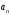 .
.
Следствие
2.5. Если
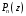 с целыми коэффициентами и
с целыми коэффициентами и
 ( приведенный многочлен), то рациональными
корнями этого многочлена могут быть
только целые числа, которые являются
делителями свободного члена
( приведенный многочлен), то рациональными
корнями этого многочлена могут быть
только целые числа, которые являются
делителями свободного члена
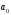 .
.
Теорема
2.7. (теорема
Виета)
Корни
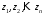 уравнения
уравнения
 связаны с его коэффициентами формулами
Виета:
связаны с его коэффициентами формулами
Виета:
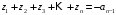 ,
,
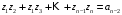 ,
,
 ,
,
………………………………….
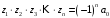 .
.
Пример
1.
Разложить многочлен на неприводимые
множители в R
и линейные множители в С,
используя схему Горнера. Сделать
проверку.
 .
.
Решение:
У нас многочлен четвертой степени, из
основной теоремы, алгебры следует, что
у него имеется ровно четыре корня. Так
как у многочлена с действительными
коэффициентами корни являются делителями
свободного члена, то делителями
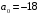 являются числа :
являются числа :
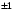 ,
,
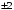 ,
,
 ,
,
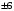 ,
,
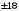 .
.
По
схеме Горнера выясним, какие из них
являются корнями многочлена
 .
.
|
|
1 |
1 |
−3 |
3 |
−18 |
|
1 |
1 |
2 |
−1 |
2 |
−16 |
|
−1 |
1 |
0 |
−3 |
6 |
−24 |
|
2 |
1 |
3 |
3 |
9 |
0 |
|
−2 |
1 |
1 |
1 |
7 |
|
|
3 |
1 |
6 |
19 |
64 |
|
|
−3 |
1 |
0 |
3 |
0 |
|
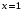 не
является корнем;
не
является корнем;
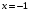 не является корнем;
не является корнем;
 − корень;
− корень;
 не является корнем;
не является корнем;
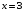 не является корнем;
не является корнем;
 − корень.
− корень.
Итак:
 − разложение
в R.
− разложение
в R.
 ,
,

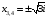 ,
отсюда
,
отсюда
 −
разложение в С.
−
разложение в С.
Проверка:
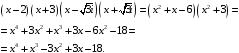
2.1. Разделить:
1.
 на
на
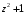 ;
;
2.
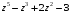 на
на
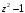 ;
;
3.
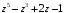 на
на
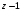 ;
;
4.
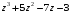 на
на
 ;
;
5.
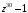 на
на
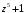 ;
;
6.
 на
на
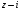 .
.
2.2. Выделить целую и дробную часть рациональной функции:
1.
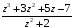 ;
2.
;
2.
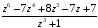 ;
3.
;
3.
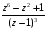 ;
4.
;
4.
 .
.
2.3. Решить уравнения:
1.
 ;
;
2.
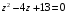 ;
;
3.
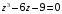 ;
;
4.
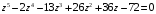 ;
;
5.
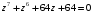 ;
;
6.
 .
.
2.4. Доказать, что целые корни алгебраического уравнения с целыми коэффициентами являются делителями свободного члена.
2.5. Найти целые корни уравнений:
1.
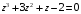 ;
2.
;
2.
 ;
;
3.
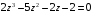 ;
4.
;
4.
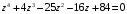 ;
;
5.
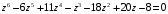 ;
6.
;
6.
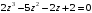 .
.
2.6.
Доказать, что каждый рациональный корень
алгебраического уравнения с целыми
коэффициентами представим в виде
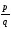 ,
где p
−
делитель свободного члена, q
−
делитель старшего коэффициента уравнения
,
где p
−
делитель свободного члена, q
−
делитель старшего коэффициента уравнения
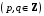 .
.
2.7. Найти рациональные корни уравнений:
1.
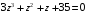 ;
;
2.
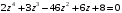 .
.
2.8.
Доказать, что если уравнение
 с действительными коэффициентами имеет
корень
с действительными коэффициентами имеет
корень
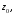 то
то
 является тоже корнем этого уравнения.
является тоже корнем этого уравнения.
2.9. Доказать, что каждый многочлен нечетной степени с действительными коэффициентами имеет, по крайней мере, один действительный корень.
2.10.
При каких значениях а
и b
число
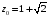 является корнем уравнения
является корнем уравнения
 ?
?
2.11.
Определить кратность корня
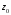 :
:
1.
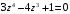 ,
,
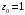 ;
;
2.
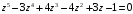 ,
,
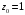 ;
;
3.
 ,
,
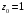 ;
;
4.
 ,
,
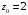 .
.
2.12. Найти приведенный многочлен наименьшей степени с действительными коэффициентами, корнями которого являются:
1.
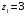 и
и
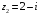 ;
;
2.
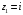 (корень кратности 2) и
(корень кратности 2) и
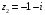 .
.
2.13.
Доказать, что если
 корни уравнения
корни уравнения
 ,
то они связаны с коэффициентами уравнения
формулами Виета:
,
то они связаны с коэффициентами уравнения
формулами Виета:
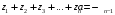
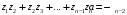

……………………………………
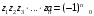 .
.
2.14.
Уравнение
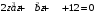 :
:
1. имеет
корни
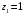 ,
,
 ;
;
2. имеет
корни
 ,
,
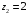 .
.
Найти третий корень уравнения.
2.15. Записать уравнение, корнями которого являются:
1.
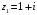 ,
,
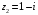 ,
,
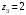 ,
,
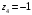 ;
;
2.
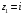 ,
,
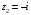 ,
,
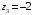 ,
,
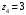 .
.
2.16. Представить многочлен в виде произведения линейных множителей:
1.
 ;
2.
;
2.
 ;
3.
;
3.
 ;
;
4.
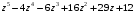 .
.
2.17. Представить многочлен в виде произведения неприводимых множителей с действительными коэффициентами:
1.
 ;
2.
;
2.
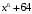 ;
3.
;
3.
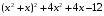 ;
;
4.
 .
.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №1