Введение

Определение 1. Назовем элементарной фигурой множество точек, представляющих собой объединение конечного числа прямоугольников со сторонами, параллельными осям координат.

Определение 2. Будем говорить, что ограниченная финитная функция обладаетI-свойством, если для любого найдется элементарная фигура площади, меньшей, содержащая все точки и линии разрыва функции.

Замечание. Множество точек плоскости назовем множеством площади нуль, если оно содержится в элементарной фигуре (или многоугольной фигуре) сколь угодно малой площади.

Теорема 1. Если ограниченная финитная функция обладаетI-свойством, то она интегрируема на плоскости в смысле Римана-Дарбу.

Доказательство . Пусть и-верхняя и нижняя грани функциии. Покроем точки линиями разрыва функцииконечным числом прямоугольников, сумма площадей которых меньше. Возьмем замкнутый прямоугольник, содержащий эту элементарную фигуру и носитель функции. Точки прямоугольника, не принадлежащие указанной элементарной фигуре, образуют множество, состоящее из конечного числа непересекающихся прямоугольников. Назовем их дополнительными. На каждом таком замкнутом прямоугольнике функци енпрерывна, а следовательно, и равномерна непрерывна. Значит существуют такие числа, что если, тодля всех, принадлежащихi-му дополнительному прямоугольнику.

Пусть . Тогда если взять разбиение дополнительных прямоугольников на частичные прямоугольники так, чтобы длина диагонали каждого из них не превосходила, то разность между верхней граньюи нижней граньюфункциинаk-ом прямоугольнике будет не больше .

Объединяя все разбиения дополнительных прямоугольников и прямоугольников построенной элементарной фигуры, определим

и

.

Тогда ,

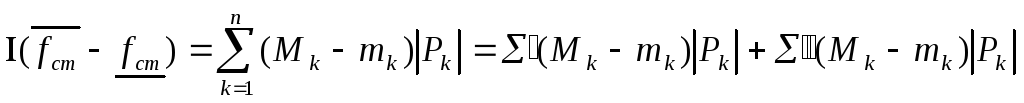где в сумму отнесены слагаемые, отвечающие прямоугольникам, покрывающим точки разрыва, а в сумму-все остальные.

Поскольку для любогоk, то

.

Далее,

.

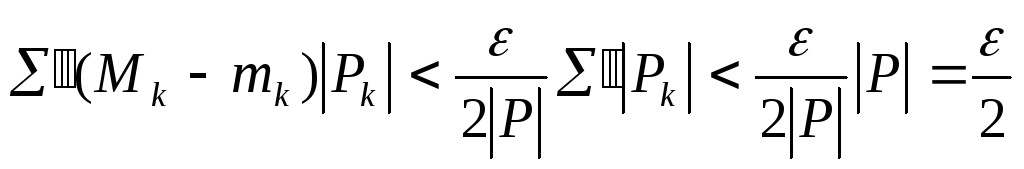Таким образом,

.

Согласно критерию интегрируемости, функция f интегрируема.

§ 1. Двойной интеграл по области.

Докажем вспомогательную лемму.

Лемма. Пусть функция одной переменной определена и непрерывна на отрезке, Г-график функции. Тогда для любогонайдется элементарная фигура площади, меньшей, содержащая Г.

Доказательство. Как доказано ранее функция интегрируема на отрезке. Следовательно, для любогонайдутся ступенчатые функциитакие, что.

Осталось заметить, что множество точек плоскости представляет собой элементарную фигуру, площадь которой равна.

Теорема доказана.

Пусть функции инепрерывны на отрезкеи областьD задана неравенствами: , то есть областьD ограничена слева и справа прямыми и, сверху графиком функции, а снизу - графиком. Заметим, что отрезки вертикальных прямых могут вырождаться в точки. Области такого вида назовем трапецией первого типа. Аналогично определяются трапеции второго типа.

Определение . Пусть функция определена в областиD. Определим

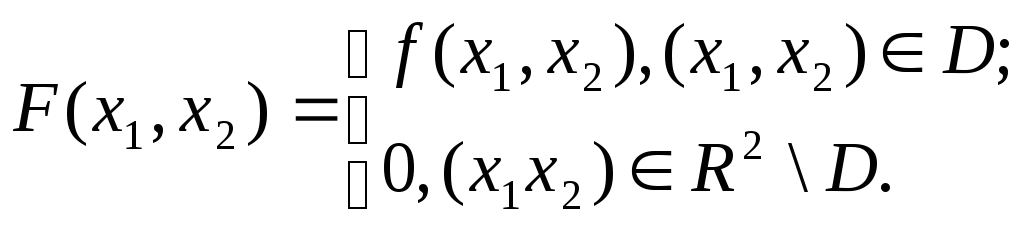
Функцию назовем интегрируемой в областиD, функция F интегрируема на плоскости .

Число назовем двойным интегралом от функциипо области D и обозначим .

Теорема 1. Пусть D-трапеция первого типа, функцияопределена и непрерывна вD. Тогда интегрируема вD и

(при этом повторный интеграл в правой части равенства существует).

Доказательство. Построим функцию F согласно определению 1. В силу леммы функция F обладает -свойством, а следовательно интегрируема. Кроме того при всехфункцияF интегрируема по переменной и

.

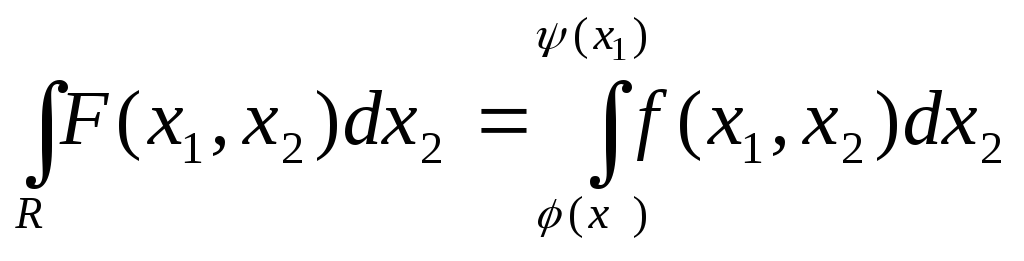Согласно следствию 2 теоремы 2 п. 5.4, повторный интеграл

.

Осталось заметить, что

при .

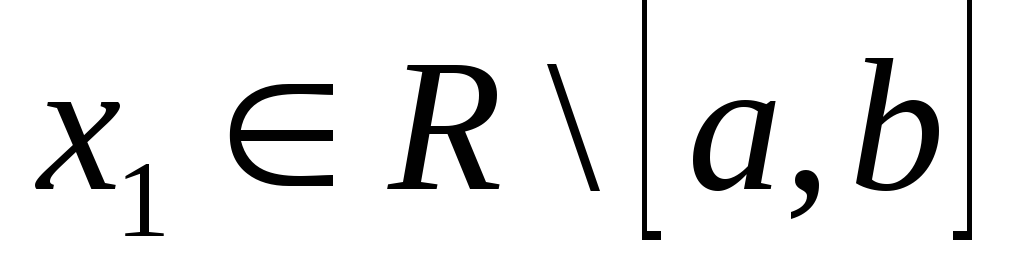Итак,

.

Теорема доказана.

Задание. Поменяв ролями и, дать определение трапеции второго типа, сформулировать аналогичную теорему для нее.

§ 2. Основные свойства двойного интеграла.

Свойства двойного интеграла вполне аналогичны соответствующим свойствам однократного определенного интеграла.

1. Аддитивность. Если функция интегрируема в областиD и область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области и , то функция f интегрируема в каждой из областей и , причем

. (*)

Замечание. Справедливо и обратное: из интегрируемости функции f в каждой из областей и следует интегрируемость функции в области D и справедливость формулы (*).

2. Линейность интеграла. Пусть функции иинтегрируемы в областиD, и-произвольные вещественные числа. Тогдаинтегрируема в областиD и

.

3. Если функции иинтегрируемы в областиD, то произведение интегрируемо в.

4. Монотонность интеграла. Если функции иинтегрируемы в областиD и всюду в , то

5. Оценка модуля интеграла. Если функция интегрируема ви

.

Замечание. Обратное неверно: из интегрируемости не вытекает интегрируемость.

6. Если функция интегрируема в, аограничена и совпадает свсюду в, за исключением множества точек площади нуль, то иинтегрируема в.

7. Теорема о среднем значении.

Если функции иинтегрируемы в областиD, функция неотрицательна (неположительна) всюду в,,, то найдется числотакое, что справедливо равенство:

.

Если при этом функция непрерывна в, асвязное множество, то внайдется такая точка, что.

8. Геометрические свойства.

Введем понятие площади плоского множества . Рассмотрим всевозможные многоугольные фигуры, целиком содержащая. Нижней площадьюназывают число

,

а верхней площадью:

,

(где -площадь).

Говорят, что имеет площадь (то есть квадрируемо), если. При этомназывают площадью.

Нетрудно сделать вывод, что

.

Если область не является трапецией первого или второго типа, то часть удается разбить на конечное число областей такого типа, не имеющих общих внутренних точек. Тогда интеграл по областив силу свойства аддитивности равен сумме интегралов по составляющим областям.