§ 3. Кратный интеграл фурье
Здесь мы дадим
лишь самые начальные понятия о кратном
ин» теграле Фурье. Пусть функция N
переменных
f(x)=f(x1,
х2,
... , хN),
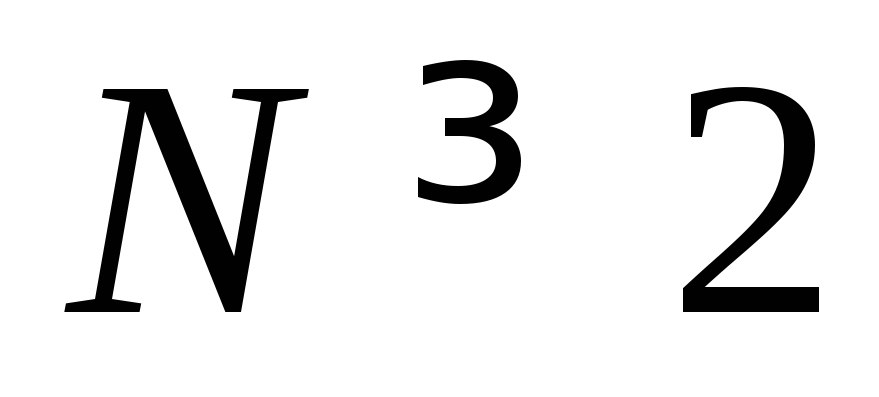 ,
такова, что существует несобственный
интеграл
,
такова, что существует несобственный
интеграл
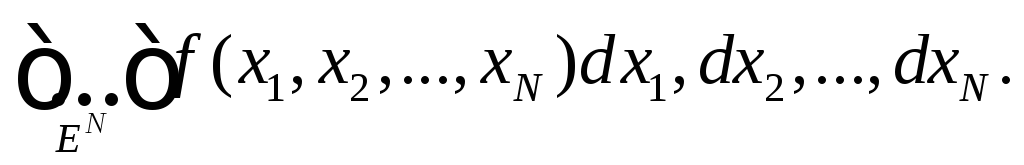
Назовем
преобразованием
(образом)
Фурье
такой функции f(х)
величину

где (х,λ)
означает скалярное произведение векторов
x=(x1,
х2,
...
...,
xN)
и λ
=(
λ1,
λ2,
…,
λN),
т. е.
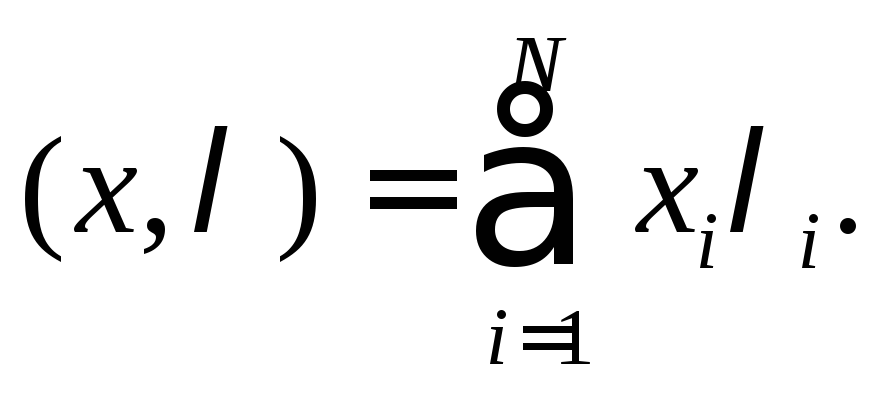
Точно так же, как
в § 1, можно показать, что g(λ)
является
непрерывной функцией λ
в ЕN
и стремится
к нулю при
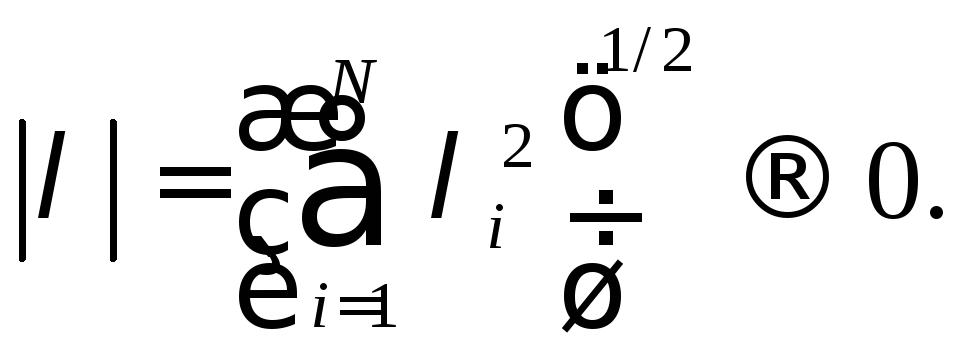 Предел
Предел
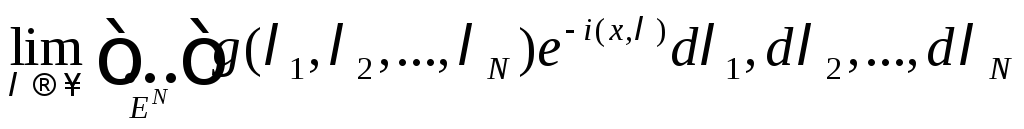
при условии, что
он существует, называется разложением
функции
f(x)
в N-кратный
интеграл
Фурье.
С помощью перехода к пределу получается
(так же, как в случае одной переменной
х) формула
обращения
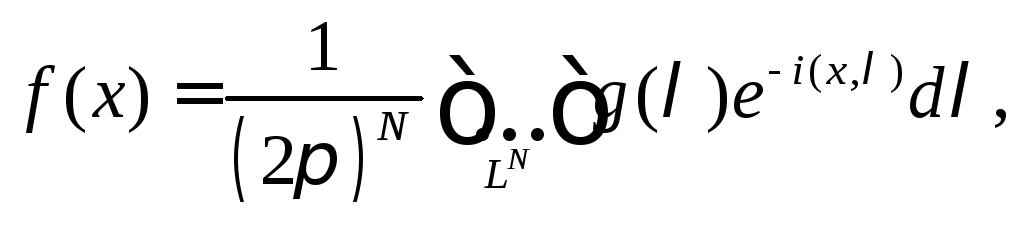
где
x=(x1,
x2,…,xN),
λ=(λ1,
λ2,…,
λN
).


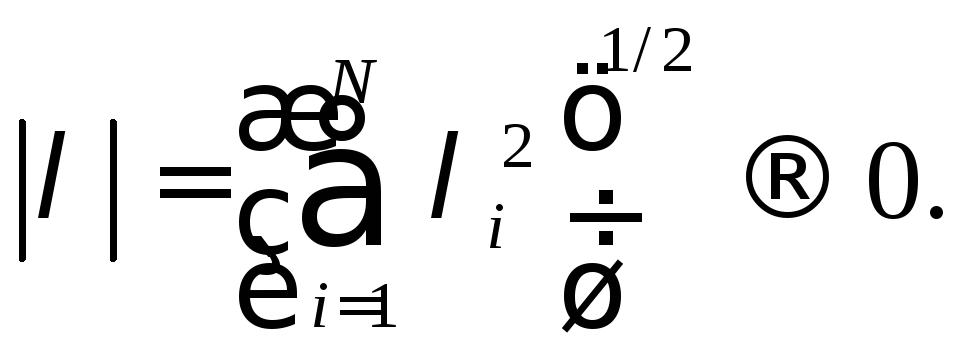 Предел
Предел