5.Булевы ф-ии

1) функции одной, 2 ^–х

2)св-ва булевых операций

1) A&A = A, A∨A = A – идемпотентность.

2) A&B = B&A, A∨B = B∨A – коммуттативность

3) A&(B&C) = (A&B)&C, A∨(B∨C) = (A∨B)∨C – ассоциотивность

4) A&(A∨B) = A, A∨A&B = A – поглошение.

5) A&(B∨C) = A&B ∨A&C, A∨B&C = (A∨B)&(A∨C) — дистрибутивность

6) ¬¬A = A – инволюция

7) Свойство констант: A&1 = A, A&0 = 0, A∨1 = 1, A∨0 = A

8) Закон исключения третьего и закон противоречия A∨¬A = 1, A&¬A = 0

9) Правило де Моргана ¬(A&B) = ¬A ∨ ¬B, ¬(A∨B) = ¬A & ¬B

Иногда к ним добавляют связь импликации и дизъюнкции

10) A→B = ¬A∨B

3) ф-ии n-переменных Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

4) Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2²ⁿ.

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2ⁿ, где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2^m=2²ⁿ.

5)задание ф-й формулами Так же, как составные высказывания строятся из более простых, с помощью логических операций, можно комбинировать булевы переменные с помощью булевых опе­раций, получая булевы выражения, которые называются формулами.

Всякой формуле однозначно соответствует некоторая функция, при этом говорят, что формула реализует функцию.

6)суперпозиция7)СДНФ СКНФ

8)представление полиномом жегалкина

9)методы нахождения полиномов

10)функц полнота

11)полная с-ма операций

В алгебре множеств для каждогоопределено дополнение, где- единица алгебры.  Таким образом, в кольце множеств полной системой операций может быть, например, пара операцийи, а в алгебре множеств нужно ещё добавить нульарную операцию(единичный элемент).

12)классы Поста

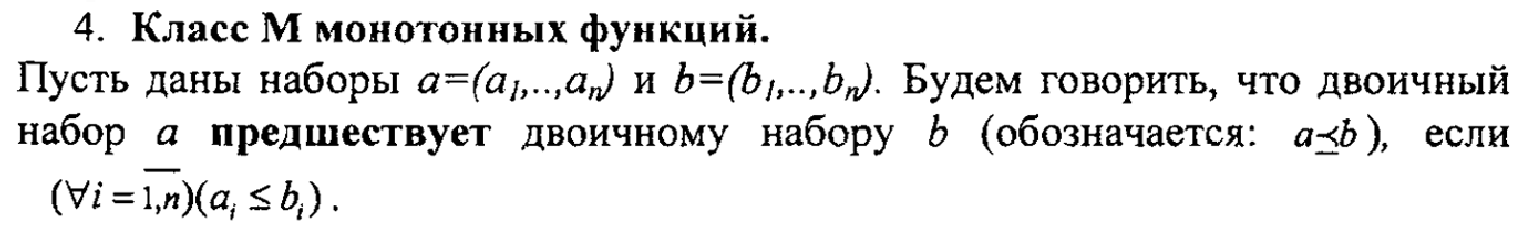
13)замкнутость классов

14)Леммы о функ-ях за…

.

15)критерий полноты

16)предполнота

6.Графы

1)Основные понятия

2)Смежность, инцидентность

3)соседство

4)степени

5)Способы задания

6)виды: Граф называется плоским (планарным), если его можно уложить на плоскости так, чтобы его ребра нигде не пересекались, кроме как в вершинах. Двудольный граф (или биграф, или чётный граф) — это граф G(V,E), такой что множество вершин V разбито на два непересекающихся подмножества V1 и V2, причём всякое ребро E инцидентно вершине из V1 и вершине из V2 (то есть соединяет вершину из V1 с вершиной из V2) Два графа G=(X,U) и L=(X',U') являются изоморфными, если между парами множеств их вершин, ребер и дуг существуют взаимно однозначные соответствия, сохраняющие смежность и ориентацию для дуг

7)абстрактный и конкретный граф Абстрактный граф- класс изоморфных графов.

8)изоморфизм

9)оценка числа графов

10)Лемма рукопожатиях и ее следствия

11) маршруты, цепи. циклы

12)Эйлеровы графы

13)критерий Эйлеровости

14)гамильтоновы