8.3 Решение дифференциальных уравнений с переменными коэффициентами.
С помощью преобразования Лапласа можно выполнить интегрирование некоторых видов линейных дифференциальных уравнений с переменными коэффициентами.
Пусть задано дифференциальное уравнение:
Рассмотрим
случай, когда коэффициенты этого
уравнения
являются полиномами отt,
тогда это уравнение может быть
преобразовано по Лапласу, если
воспользоваться теоремой дифференцирования
изображения.
……………………………………………………….
Подставляя
в уравнение полученные результаты,
можно убедиться, что исходное
дифференциальное уравнение преобразуется
в дифференциальное уравнение относительно
,
но это уже будет обыкновенное линейное
дифференциальное уравнение. Порядок
этого уравнения будет такой, какова
наивысшая степеньt
имеющаяся
в исходном уравнении.
Целесообразность преобразования по Лапласу в том, что преобразованное дифференциальное уравнение оказывается более простым, чем исходное.
Пример. Найти общее решение дифференциального уравнения
или
.
Получим линейное дифференциальное уравнение 1 порядка. Решим его методом Бернулли с помощью подстановки X=UV. При этом уравнение примет вид:
Согласно методу Бернулли будем иметь:
Тогда изображения искомого решения примет вид:
Возвращаясь к оригиналу, получим
8.4 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
Пусть дана система n дифференциальных уравнений 2го порядка.
, (8.9)
где
–к-тая
функция, которую необходимо найти,
-
коэффициенты системы,
-
правые части.
Пусть заданы начальные условия
Пусть
Применяя к обеим частям каждого уравнения преобразование Лапласа, получим систему:
,
Эта
алгебраическая система относительно
неизвестных
.
Решим её и затем переходим к оригиналам.
Пример. Решить систему
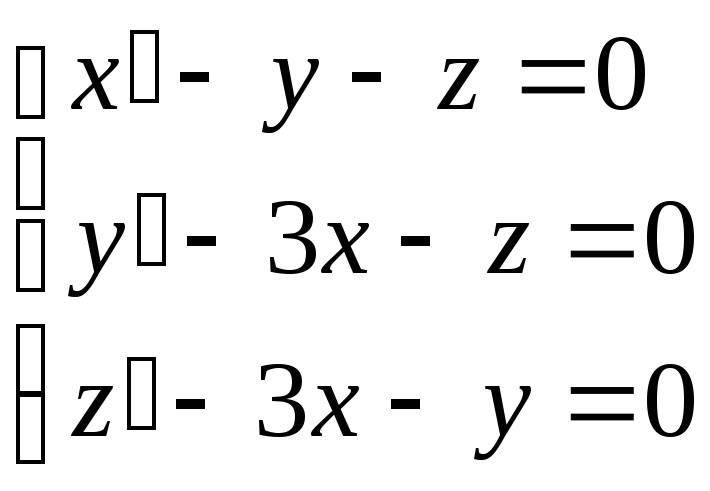
При начальных условиях x(0)=1, y(0)=0, z(0)=-1.
Решение:
Пусть
,
,
В области изображений система примет вид:
или
Решим систему:
.
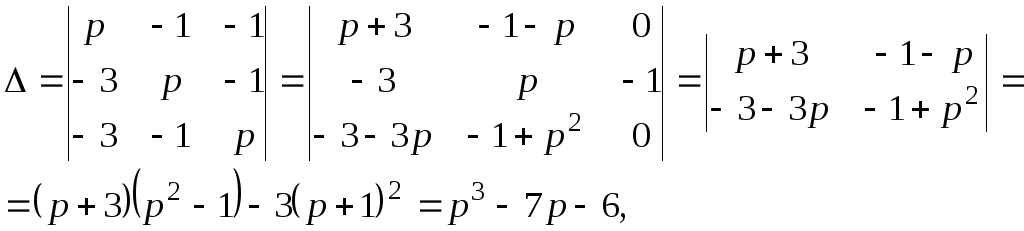
Аналогично найдутся и другие функции y(t) и z(t). Для решения системы дифференциальных уравнений операторным методом требуется решить только одну систему линейных алгебраических уравнений. При этом учитываются и начальные условия. Следует отметить возможность нахождения каждой неизвестной функции независимо от других. Проделать тоже самое классическим методом весьма затруднительно.
8.5 Линейные дифференциальные уравнения с запаздывающим аргументом.
В ряде технических задач приходится иметь дело с дифференциальными уравнениями, в которых неизвестная функция входит при различных значениях аргумента, например:
и т.п.
Такие уравнения называются дифференциальными уравнениями с отклоняющимися аргументами.
Если
постоянные, то мы имеем так называемое
дифференциально – разностное уравнение.
Если
и старшая производная входитв
дифференциально-разностное
уравнение
только при одном значении аргумента,
не меньшем всех других аргументов
функций и производных, входящих в
уравнение, то уравнение называют
дифференциальным
уравнением с запаздывающим аргументом.
Пусть дано дифференциальное уравнение с запаздывающим аргументом с постоянными коэффициентами
,
где
=const,
.
Возьмем для простоты нулевые начальные условия
.
Применяя преобразования Лапласа, получим
.
Откуда найдем
от изображения переходим к оригиналу x(t).
Пример: Решить уравнение.
.
Решение:
В
области изображений
откуда
Переходим
к оригиналу
.