4) Интервальные оценки для значимых парных коэффициентов корреляции.

Для каждого значимого коэффициента корреляции построим интервальные оценки. Для этого воспользуемся Z - преобразованием Фишера (5):

Z=0,5 ln.

Из математической статистики известно, что при небольших n распределение величины Z хорошо приближается нормальным распределением с математическим ожиданием равным

(6)

и дисперсией , откуда следует, что стандартное отклонение равно .

Вычислим критическое значение критерия Стьюдента t для заданного уровня значимости  по статистическим таблицам или с помощью встроенной функции электронных таблиц.

Тогда доверительный интервал для коэффициента корреляции принимает вид:

( M [r] - d; M [r] + d ), или (7)

5) Коэффициент корреляции рангов.

К мерам тесноты парной связи относится и предложенный английским психологом Ч. Спирменом (1863-1945) коэффициент корреляции рангов.

Ранги - это порядковые номера единиц совокупности в ранжированном ряду. Если проранжировать совокупность по двум признакам, связь между которыми изучается, то полное совпадение рангов означает максимально тесную связь, а полная противоположность рангов - максимально тесную обратную связь. Ранжировать оба признака следует в одном и том же порядке: либо от меньших значений признака к большим, либо наоборот. Если ранги единиц совокупности по признакам х и у обозначить как Р_x , Р_y , то коэффициент корреляции рангов принимает вид:

(8)

Известно, что средние ранги вычисляются по формуле (n+1)/ 2. Также известно, что сумма квадратов отклонения чисел натурального ряда от их средней величины

и равна . (9)

Следовательно, знаменатель формулы (8) равен

Рассмотрим далее разности рангов d_i = и сумму их квадратов отклонений:

=

Откуда следует

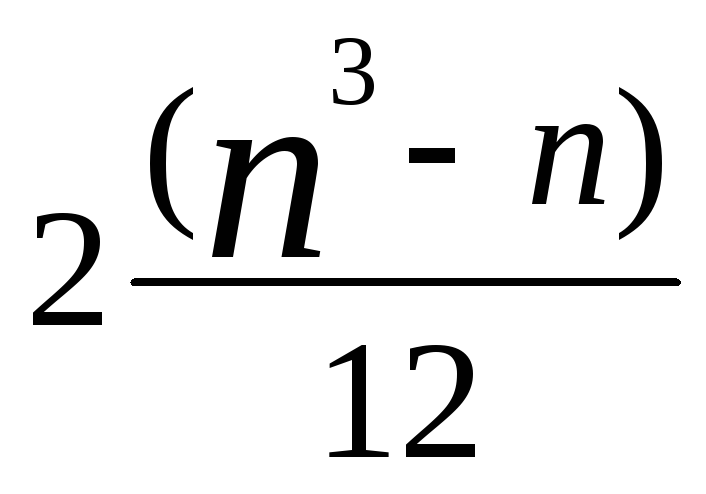- : 2 = - (10)

Подставив (10) в (8) , получим

(11)

Формула (11) представляет собой формулу Спирмена.

Преимущество коэффициента корреляции рангов состоит в том, что ранжировать можно и по таким признакам, которые нельзя выразить численно.

Недостатком коэффициента корреляции рангов является то, что одинаковым разностям рангов могут соответствовать совершенно отличные разности значений признаков (в случае количественных признаков). Поэтому для последних следует считать корреляцию рангов приближенной мерой тесноты связи, обладающей меньшей информативностью, чем коэффициент корреляции числовых значений признаков.

Если среди значений признаков х и у встречаются несколько одинаковых, то образуются связанные ранги, т.е. одинаковые средние номера. Например, вместо одинаковых по порядку третьего и четвертого значений признака будут записаны 2 ранга по (3+4)/2=3,5.