
Замараев - часть 1
.pdf
k1 ×a = A ×(- k1 + k2 ) , |
|
|||||
|
|
ß |
|
|
|
|
|
A |
= |
k1 ×a |
, |
|
|
|
k2 - k1 |
|
||||
|
|
ß |
× (e−k1t - e−k2t ). |
|
||
C |
= |
k1 × a |
(3.10) |
|||
|
||||||
|
A2 |
k2 - k1 |
|
|
||
|
|
|
|
|||
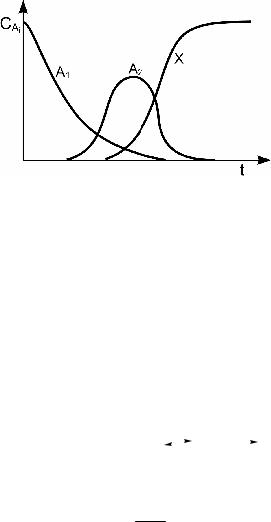
3. Графики зависимости концентраций различных веществ от времени качественно будут иметь вид (рис. 3.1):
Рис. 3.1. Графики зависимости концентраций различных веществ от време- ни для последовательной реакции A1 ® A2 ® A3 ® A4 ® A5 ® X
Существенно, что концентрация исходного вещества A1 монотонно убывает во времени, концентрация конечного про- дукта монотонно возрастает во времени, а концентрации всех промежуточных веществ проходят через максимум. При этом концентрация первого промежуточного продукта A2 при малых t является линейной функцией t:
dCA2 |
|
= k1 |
×a , |
dt |
|
||
|
t=o |
|
|
|
|
|
а концентрации всех остальных промежуточных веществ при малых t не являются линейными функциями t.
Отмеченные закономерности могут быть использованы для того, чтобы судить на качественном уровне о некоторых осо-
68
бенностях механизмов реакций на основании вида кинетиче- ских кривых. Например, на основании кинетических зависи- мостей вида (рис. 3.2):
Рис. 3.2. Типичный при-
мер экспериментально наблюдаемых кинетиче-
ских зависимостей
Можно предположить, что A1 – исходное вещество, X – про- дукт реакции, A2 – промежуточное вещество. При этом A1 превращается в A2 не прямо, а через некоторое другое (нена- блюдаемое экспериментально) промежуточное вещество B. Об этом говорит форма кривой для A2 в области левее мак- симума. Таким образом, можно предложить следующий меха- низм для данной реакции:
A1 ¾® B ¾® A2 ¾® X .
Однако для окончательного доказательства такого меха-
низма необходим количественный анализ всех кинетических кривых.
Случай Б. Двухстадийная последовательная реакция с
одной обратимой стадией
А |
|
k1 |
В |
k2 |
Х. |
|
|
|
|
|
|||
|
k–1 |
|
||||
|
|
|
|
|
||
Здесь три реакции, но только два линейно независимых кинетических уравнения:
dCdtA = - k1 ×CA + k−1 ×CB ,
69

dCdtB = k1 × CA - (k−1 + k2 )× CB .
Третье уравнение для CX
dCdtX = k2 ×CB
является линейной комбинацией двух предыдущих: dCdtB + dCdtX = - dCdtA .
Это очевидно и из условий материального баланса, и из не- посредственных вычислений. Действительно, левая часть по-
следнего уравнения
k1 × CA - k−1 × CB - k2 × CB + k2 × CB = k1 × CA - k−1 × CB
равняется правой
k1 × CA - k−1 × CB . Пусть при t = 0 CA = a и CB = 0.
Мы имеем систему из двух линейных уравнений первого порядка с постоянными коэффициентами.
Составим характеристическое уравнение: |
|
|
|
|
|
||||||||||||||
|
- (k1 + l) |
|
|
k-1 |
|
|
= 0, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
k1 |
|
- (k-1 + k2 + l) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
ß |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k1 + l)×(k-1 + k2 + l) - k1k-1 = 0 , |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
ß |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 ×k−1 + k1 ×k2 + k1 × l + (k−1 + k2 )× l + l2 - k1 ×k−1 = 0 , |
|||||||||||||||||||
l2 + (k |
|
|
ß |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
+ k− + k |
2 |
)× l + k |
1 |
×k |
2 |
= 0 , |
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
ß |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
l = - |
k1 + k−1 + k2 |
± |
|
|
|
(k1 + k−1 + k2 )2 |
|
- k |
1 |
×k |
2 |
. (3.11) |
|||||||
|
|
|
|||||||||||||||||
1,2 |
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
70
Ищем решение в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
CA |
|
= A × eλ1t |
+ B × eλ2t , |
|
|
CB |
= P × eλ1t + Q × eλ2t . |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
a |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Учтем, что при t = 0 |
|
|
CA = a и CB = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ì 1 = A + B |
|
|
|
|
|
|
ì B = 1- A |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Þ |
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
= P + Q |
|
|
|
|
|
|
ï |
Q = -P |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
î 0 |
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
CA |
|
= A × eλ1t + (1- A)× eλ2t , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CB |
|
= P × (eλ1t - eλ2t ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Учтем, что при t = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 |
× |
|
dC |
A |
|
= - k |
|
|
× |
|
C |
A |
|
, |
|
A × l |
|
+ (1- A)× l |
|
|
|
= -k |
|
, |
|
|
||||||||||||||||||||||||
|
a |
|
dt |
|
1 |
|
|
a |
|
1 |
2 |
|
|
1 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1 |
× |
dC |
B |
|
|
= |
|
|
k |
|
|
× |
C |
A |
, P ×(l |
|
|
- l |
|
) = k |
|
, |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
a |
|
dt |
|
|
1 |
|
|
|
1 |
|
2 |
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
ß |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 |
|
|
|
|
||
A ×(l1 - l2 ) = - k1 - l2 , |
|
|
A = k1 + l2 , |
P = |
|
|
|
|
|
|
|
|
, |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
l1 - l |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 - l1 |
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ß |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- A = l2 - l1 - k1 - l2 |
= - |
k1 + l1 |
, |
|
P = |
|
|
|
k1 |
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
l |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
2 |
|
- l |
|
|
|
|
|
|
|
l |
2 |
- l |
1 |
|
|
|
|
1 |
|
- l |
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В итоге получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
CA |
|
= |
|
k1 + l2 |
× eλ1t - |
k1 + l1 |
|
× eλ 2t, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
l |
2 |
- l |
|
|
|
|
|
l |
2 |
- l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
(3.12) |
|||||
|
|
|
|
|
|
|
|
|
|
|
CB |
|
|
|
|
|
|
|
|
|
k1 |
|
|
× (eλ1t - eλ2t ) . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 - l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
71

§ 3.4. Составление кинетических уравнений для сложных реакций. Скорости изменения концентраций, кинетические константы и константы скорости
Любая сложная реакция может быть представлена в виде сочетания обратимых, параллельных и последовательных реакций. На основании данных, изложенных в гл. 2 и преды- дущих параграфах гл. 3, можно построить систему диффе- ренциальных уравнений, описывающих кинетику любой слож- ной реакции. Алгоритм такого построения состоит в следую- щем:
1. Для любого соединения (исходного вещества, продукта реакции или промежуточного вещества) выписываются урав- нения, левая часть которых представляет собой первую про-
dCdti . (Для простоты
мы рассматриваем реакции в системе с постоянным объе- мом, V = const, поэтому именно производная от концентрации Ci по времени есть мера скорости расходования или образо- вания веществ.)
2.Для каждого вещества правая часть уравнения пред- ставляет собой сумму членов, каждый из которых представ- ляет собой правую часть закона действующих масс для ста- дии (т. е. простой реакции), в которой образуется или расхо- дуется данное вещество. Число таких членов равно числу простых реакций, в которых образуется или расходуется дан- ное вещество.
3.Член, соответствующий простой реакции, входит в пра-
вую часть уравнения для dCdti со знаком «плюс», если i-е ве-
щество в этой реакции образуется, и со знаком «минус», ес- ли оно в этой реакции расходуется.
4. Численный коэффициент при каждом члене равен числу частиц i-го вещества, образующихся или расходующихся в данной простой реакции.
72

5. Порядок простой реакции по j-му веществу, т. е. показа- тель степени nj для сомножителя Cνj j в члене, соответствую-
щем данной простой реакции, равен числу частиц j-го веще- ства, участвующих в этой реакции.
Примеры
Правильное кинетическое уравнение для обратимой ав-
токаталитической реакции
А + В |
|
k+ |
2 В |
|
|
|
|
||
|
k– |
|||
|
|
|
||
получится, если учесть, что В выступает как в роли реагента, так и продукта реакции:
|
|
dCA = -k+ ×C |
|
× C + k− ×C2 |
, |
|
|
|||||||
|
|
|
dt |
|
|
|
A |
|
B |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dCB |
= - k+ ×C ×C |
+ k− × C |
2 |
+ |
2k+ ×C ×C - 2k |
− ×C |
2 |
|||||||
dt |
|
|
||||||||||||
1444244443 |
|
14444244443 |
||||||||||||
|
|
|
A |
B |
|
|
B |
|
A |
B |
B |
|||
|
скорость изменения концентра− |
скорость изменения концентра− |
||||||||||||
|
ции в прямой реакции |
|
|
|
|
ции в обратной реакции |
|
|||||||
|
|
|
dCB = k+ ×C |
ß |
|
|
|
|
|
|
||||
|
|
|
|
|
×C - k− ×C2 . |
|
|
|
||||||
|
|
|
dt |
|
|
A |
|
B |
B |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим сложную реакцию, состоящую из шести ста- дий (простых реакций):
2 А + В |
|
k1 |
|
3 С, |
|
|
|
|
|
||
|
k–1 |
||||
|
|
|
|
||
2 С + D |
|
k2 |
|
3 B, |
|
|
|
|
|
||
|
k–2 |
|
|||
|
|
|
|
||
2 B + D |
|
k3 |
|
2 P. |
|
|
|
|
|
||
|
k–3 |
|
|||
|
|
|
|
||
Этой реакции соответствует следующая система кинетиче- ских уравнений:
73
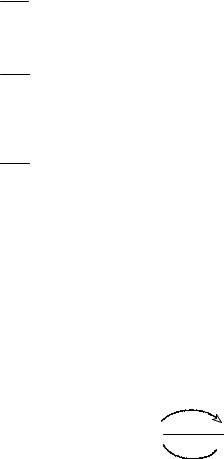
dCA = - 2 k |
|
× C2 |
× C + 2 k− |
× C3 |
, |
||
dt |
|
1 |
A |
B |
1 |
C |
|
|
|
|
|
|
|
||
dCdtB = -k1 × C2A × CB + k−1 ×C3C + 3 k2 × C2C × CD - 3 k−2 ×CB3 - 2 k3 ×CB2 ×CD + 2 k−3 × CP2 ,
dCdtC = 3 k1 × C2A × CB - 3 k−1 ×C3C - 2 k2 × CC2 ×CD + 2 k−2
-
× CB3 ,
dCD |
= - k |
|
× C2 |
× C |
|
+ k |
−2 |
× C3 |
- k |
|
×C2 |
× C |
|
+ k |
−3 |
× C2 |
, |
dt |
|
|
|
|
|||||||||||||
|
2 |
C |
|
D |
|
B |
|
3 |
B |
|
D |
|
P |
|
dCdtP = 2 k3 ×CB2 × CD - 2 k−3 ×CP2 .
Производную в левой части каждого из этих уравнений на-
зывают скоростью изменения концентрации данного вещества.
Константы ki, где i изменяется от –3 до 3, называют кон-
стантами скорости.
Любую комбинацию констант скорости называют кинетической константой. Например, в выражении (3.6)
CA = a × e−(k1 +k2 +k3 )t
для изменения концентрации вещества A в ходе параллель-
ной реакции
k1
Ak2 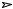 X k3
X k3 
величина k = k1 + k2 + k3 является кинетической константой. Для рассматриваемой реакции из зависимости CA от t можно определить только k, но нельзя определить порознь констан- ты скорости k1, k2 и k3.
74
§ 3.5. Метод квазистационарных концентраций
Для того чтобы обойти трудности, связанные с решением громоздких систем кинетических уравнений, применяется весьма эффективный приближенный метод – метод квазиста- ционарных концентраций. Его физической основой является тот факт, что компоненты сложной реакции – исходные, конеч- ные и промежуточные вещества – отличаются не только по на- званию: промежуточные вещества потому и не являются ко- нечными продуктами, что они в данных условиях достаточно быстро вступают в дальнейшие реакции, то есть время их жиз- ни часто много меньше времени жизни остальных веществ.
1. Вернемся в качестве примера к последовательной ре-
акции
А |
|
k1 |
В |
k2 |
Х, |
|
|
|
|
|
|||
|
k–1 |
|
||||
|
|
|
|
|
||
рассмотренной в § 3.3. Применительно к этой реакции усло- вие, что время жизни промежуточного вещества много мень- ше, чем время жизни остальных веществ, означает, что
k-1 + k2 >> k1.
Тогда выражение (3.11) для характеристических корней
l = - |
k1 + k−1 + k2 |
± |
|
(k1 + k−1 + k2 )2 |
- k |
1 |
×k |
2 |
= |
||||||
|
|
|
|||||||||||||
1,2 |
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
é |
|
|
|
|
|
|
|
|
|
ù |
|
|
k1 + k−1 + k2 |
|
|
|
|
|
4 k1 ×k2 |
|
|
|
|
||||
= - |
× ê |
1m 1- |
|
|
|
|
ú |
|
|||||||
|
(k1 |
|
|
2 |
|
|
|||||||||
|
|
2 |
|
ê |
|
|
|
+ k−1 + k2 ) |
ú |
|
|||||
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
û |
|
существенно упрощается. Действительно, при k-1 + k2 >> k1 имеем
|
|
é |
|
|
|
|
|
ù |
|
|
k−1 + k2 |
|
|
4 k1 ×k2 |
|
|
, |
||
l1,2 = - |
× ê |
1m |
1- |
|
ú |
||||
|
|
2 |
|||||||
2 |
ê |
|
|
( k−1 + k2 ) |
ú |
|
|||
|
|
|
|
||||||
|
|
ë |
|
|
|
|
û |
|
|
причем
75

k1 ×k2 2 <<1 . (k−1 + k2 )
В этом случае корень квадратный в правой части выражения для l1,2 можно разложить в ряд Тейлора, ограничившись пер- выми двумя членами:
1- |
4 k1 ×k2 |
|
|
= 1- |
1 |
× |
4 k1 ×k2 |
|
= 1- |
2 k1 ×k2 |
|
. |
( k−1 + k2 ) |
2 |
2 |
( k−1 + k2 ) |
2 |
( k−1 + k2 ) |
2 |
||||||
|
|
|
|
|
|
|
|
|
Подставляя это выражение в выражение для l1,2, получаем
|
k−1 |
+ k2 |
é |
æ |
|
2 k1 ×k2 |
|
ö ù |
||
l1,2 = - |
× ê |
ç |
- |
|
÷ |
ú = |
||||
|
|
1m ç1 |
|
|
|
÷ |
||||
|
2 |
( k− |
|
2 |
||||||
|
|
ê |
è |
|
+ k ) |
ø |
ú |
|||
|
|
|
|
1 |
2 |
|
||||
|
|
|
ë |
|
|
û |
||||
ì |
|
|
|
- |
|
|
k1 ×k2 |
|
|
|
|
|
|
|
|
|||||
ï |
|
|
|
|
|
( k−1 + k2 ) |
|
|
|
|
|
|
|
|||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
- |
2 (k− |
1 |
+ k |
2 |
) |
+ |
k |
1 |
×k |
2 |
|
|
|
|
|||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
( k−1 + k2 ) |
|
|||||||||||
î |
|
|
|
|
|
|
|
|
|
|
||||||||||
Как видим, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
1 |
|
|
= |
|
k1 ×k2 |
|
<< |
|
l |
2 |
||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
k−1 + k |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ì |
|
k1 |
×k2 |
|
|
|
|
|
ï- |
|
|
|
|
|
|
|
|
( k− |
|
+ k |
|
) |
|
||
= |
ï |
|
|
2 |
. |
|||
í |
|
|
1 |
|
||||
|
ï |
|
|
|
|
|
|
|
|
ï |
- (k−1 |
+ k2 ) |
|
||||
|
î |
|
||||||
= k−1 + k2 .
В этом случае в выражениях для CA и CB
ék |
1 |
+ l |
2 |
λ t |
|
k |
1 |
+ l |
1 |
|
λ |
t ù |
|
|||
CA = a × ê |
|
|
|
× e 1 |
- |
|
|
× e |
2 |
ú |
, |
|||||
|
|
|
|
|
l2 - l1 |
|||||||||||
ël2 - l1 |
|
|
|
û |
(3.14) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CB = a × |
|
k1 |
|
× (eλ1t - eλ2t ) |
|
|
|
|||||||||
l1 - l2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
начиная с некоторых достаточно больших значений t будет
выполняться условие
eλ1t >> eλ2t ,
т. е. можно пренебречь членами, содержащими eλ 2t .
76
При этом получаем
CA = a × k1 |
+ l2 |
||
|
l2 - l1 |
||
CB = a × |
|
k1 |
|
l1 |
- l2 |
||
|
|||
Учтем, что:
1) k1 + l2 = k1 – (k–1 + k2) » –(k–1 2) l2 – l1 » l2 = –(k–1 + k2) .
Тогда получим
×el1t ,
×el1t .
+k2);
|
|
|
|
- |
|
k1×k2 |
× t |
|
|
|
||
|
CA = a × e |
k−1+ k2 |
; |
|
||||||||
|
|
|
k |
|
|
- |
|
k1×k2 |
|
|||
|
|
|
1 |
|
k− |
+ k |
|
|||||
CB = a × |
|
|
|
× e |
1 |
|
|
2 |
||||
k-1 + k2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CB |
= |
|
k1 |
|
|
×CA |
. |
|
|||
|
|
|
|
|
|
|||||||
|
|
|
k-1 + k2 |
|
|
|
|
|||||
(3.15)
× t
,(3.16)
(3.17)
Таким образом, мы получили легко анализируемые урав- нения как для CA, так и для CB.
2. Теперь заметим, |
|
что |
|
соотношение |
CB = |
k1 |
×CA |
||||||||||||||||
|
|
k-1 |
+ k2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
можно получить из исходных кинетических уравнений |
|
|
|||||||||||||||||||||
|
|
dCA |
|
= - k |
1 |
×C |
A |
+ k |
−1 |
× C |
B |
, |
|
|
|
||||||||
|
|
dt |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
dCB |
= k |
1 |
× C |
A |
- k |
-1 |
× C - k |
2 |
×C |
B |
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
dt |
|
|
|
|
|
|
B |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сразу, положив |
dCB |
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
77
