2.2 Алгоритм Флойда-Уоршелла

Задан ориентированный взвешенный граф. Требуется построить для этого графа матрицу кратчайших путей между всеми парами вершин.

Алгоритм решения.

Пусть веса дуг заданы в виде матрицы D. Будем решать задачу методом динамического программирования. Обозначим за 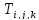длину кратчайшего пути между вершинами i и j, который в качестве промежуточных содержит только вершины с номерами, не превосходящими k. Рассмотрим случай, когда k=0. Это означает, что промежуточных вершин в путях быть не может. Значит, путь будет существовать между теми вершинами, между которыми по условию есть дуга. Тогда матрицу 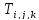построим на основе матрицы D следующим образом. Во-первых, расстояние между вершинами, между которыми нет дуги, положим равным бесконечности. Во-вторых, из вершины в неё саму всегда можно добраться за нулевое число шагов, поэтому если вес дуги (i,j)  положителен, то заменим его нулём. Пусть теперь k>0. Понятно, что искомый кратчайший путь может либо проходить через вершину с номером k, либо нет. Если он проходит через эту вершину, то его можно разбить на две части: путь от i до k и путь от k до j. Поскольку оба этих пути должны являться кратчайшими, имеем следующее рекуррентное соотношение:

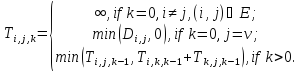
Асимптотическая сложность алгоритма – O(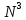), где N – число вершин графа.

Так же, как и в алгоритме Форда-Беллмана, объём используемой памяти можно сократить. Нам достаточно одной матрицы размерности N. Все обновления расстояний мы будем осуществлять именно в ней.

Отметим, что при наличии в графе циклов отрицательного веса существуют кратчайшие пути сколь угодно малого веса. Имеет место следующий критерий: в графе есть циклы отрицательного веса тогда и только тогда, когда для некоторого i .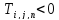

Задача 2

Дан взвешенный ориентированный граф из N вершин. Требуется найти в нем величину кратчайшего пути между каждой парой вершин.

Входные данные:

В первой строке записано натуральное число 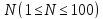. В каждой из следующих N строк записано по N чисел — матрица весов дуг графа. Все веса представляют собой целые неотрицательные числа, не превосходящие 1000. Если в матрице в i-й строке j-м столбце стоит 0, то это означает, что дуги из вершины i в вершину j нет.

Выходные данные:

В выходной файл надо вывести матрицу кратчайших путей между каждой парой вершин графа (т.е. матрицу у которой в i-й строке j-м столбце стоит длина кратчайшего пути из вершины i в вершину j или 0 — если пути из i в j не существует).

1. import java.io.PrintWriter;

2. import java.util.Scanner;

3. public class Solution {

4. private static final int INF = 1000 * 1000 * 1000; //в качестве условной бесконечности выберем достаточно большое число 10^9

5. public static void main(String[] args) {

6. Solution solution = new Solution();

7. solution.solve(); //вызываем процедуру решения задачи

8. }

9. private void solve() {

10. Scanner scanner = new Scanner(System.in);//для считывания воспользуемся классом Scanner

11. PrintWriter printWriter = new PrintWriter(System.out); //для считывания воспользуемся классом PrintWriter

12. int vertexCount = scanner.nextInt(); //cчитываем число вершин графа

13. int[][] g = new int[vertexCount][vertexCount]; //граф будем хранить в матрице смежности

14. for (int i = 0; i < vertexCount; i++) {

15. for (int j = 0; j < vertexCount; j++) {

16. g[i][j] = scanner.nextInt(); //считываем вес ребра между вершинами i и j соответственно

17. if (g[i][j] == 0) {

18. g[i][j] = INF; //по условию если g[i][j] = 0, то это означает, что дуги из i в j нет; в этом случае расстояние между этими вершинами бесконечно велико

19. }

20. }

21. }

22. for (int k = 0; k < vertexCount; k++) {

23. for (int i = 0; i < vertexCount; i++) {

24. for (int j = 0; j < vertexCount; j++) { // Согласно алгоритму будем обновлять ответ для каждой пары вершин i и j, перебирая промежуточную вершину k

25. g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]);

26. }

27. }

28. }

29. for (int i = 0; i < vertexCount; i++) {

30. for (int j = 0; j < vertexCount; j++) {

31. if (g[i][j] == INF) {

32. printWriter.print(0 + " ");

33. }

34. else {

35. printWriter.print(g[i][j] + " "); //для каждой пары вершин выведем величину кратчайшего пути от i до j, или 0, если j не достижима из i

36. }

37. }

38. printWriter.println();

39. }

40. scanner.close(); //закрытие потока ввода

41. printWriter.close(); //закрытие потока вывода

42. }

43. }