
Е. Н. Яшин Анализ и Синтез Дискретных Систем
.pdf
3.1. Канонические формы описания в пространстве состояний
Название |
|
|
At |
|
|
|
Bt |
Ct |
|
Примечание |
Диагональная каноническаяформа |
|
|
|
|
|
|
|
|
|
Все собственные |
λ1 |
|
0 |
b1, d |
c1, d |
значения λ1, λ2, …, λn |
|||||
0 L |
простые и различные |
|||||||||
|
|
λ2 L |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
b2, d |
c2, d |
|
|||
|
M |
M O M |
|
M |
M |
|
|
|||
|
|
0 0 L λn |
|
bn, d |
cn, d |
|
||||
|
|
|
|
|
|
|
|
|
||
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CT = [c |
c |
2, s |
Lc |
n, s |
] |
||
Вертикальная |
сопровождающая (формаканоническая |
|
0 |
|
|
|
|
− an |
|
|
|
|
1 |
|
|
|
|
|
|
|
t |
1, s |
|
|
|
|
||||
|
0 0 |
L |
|
|
|
|
CT B |
CT |
= [g(1) g(2)Lg(n)] |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
1 |
0 0 L − an −1 |
|
|
|
0 |
|
C |
|
AB |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
1 0 L − an − 2 |
|
|
|
|
0 |
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
M O L |
M |
|
|
|
|
M |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
0 0 1 |
|
− a |
|
|
|
|
0 |
|
CT |
An −1B |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Каноническаяформа |
0 |
|
1 |
0 |
L 0 |
|
|
0 |
|
|
bn |
|
|
|
|
|
|
|
|
|||||||||||
управляемости (нормальнаяформа) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
L |
|
|
|
0 |
|
|
bn −1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
0 |
|
0 |
0 |
O M |
|
|
|
0 |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n − 2 |
|
|
|
|
|
|
|
|
|
||
|
|
M |
|
M |
M |
L |
1 |
|
|
|
M |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|||
|
− a |
n |
− a |
n−1 |
− a |
n −2 |
L − a |
|
|
|
1 |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BT |
= [b |
b |
|
Lb |
|
] |
|
Горизонтальная |
сопровождающая (формаканоническая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
1, B |
2, B |
|
n, B |
|
||
|
|
0 |
|
1 |
0 |
L |
0 |
CT B |
|
|
1 |
|
BT |
= [g(1) g(2)Lg(n)] |
||||||||||||||||
|
0 |
|
|
|
|
|
L 0 |
|
|
|
|
|
|
|
0 |
|
t |
|
|
|
|
|
|
|
||||||
|
|
0 |
1 |
CT AB |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
0 |
0 |
O M |
|
|
|
M |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
M |
M |
L |
1 |
|
|
|
M |
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
||||
|
− a |
n |
− a |
n−1 |
− a |
n −2 |
L − a |
|
CT |
An −1B |
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Каноническаяформа наблюдаемости |
|
0 |
0 0 L − an |
|
|
bn |
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
0 0 L − a |
n −1 |
|
|
|
b |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 0 L − a |
|
|
|
|
n −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 |
n − 2 |
|
|
|
b |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
M |
M O L |
M |
|
|
|
|
M |
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
0 0 1 |
|
− a |
|
|
|
|
b |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59
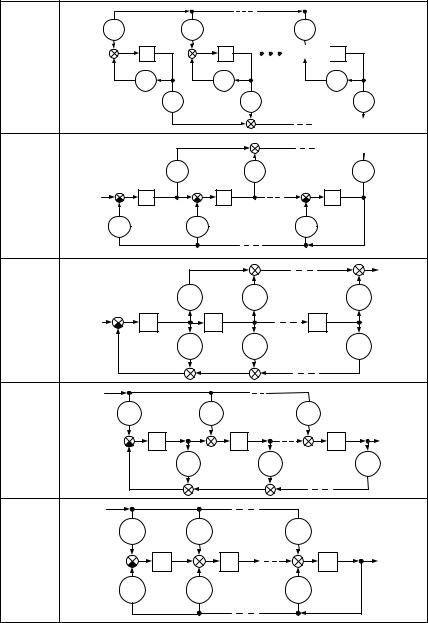
Диагональная |
каноническая форма |
||
Вертикальная |
сопровождающая |
каноническаяформа) |
|
|
|
|
( |
Каноническая форма |
управляемости |
(нормальная форма) |
|
Горизонтальная |
сопровождающая |
каноническаяформа) |
|
|
|
|
( |
Каноническая форма |
наблюдаемости |
||
u(k) 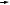

bn ,d |
b |
b |
|
n−1,d |
1,d |
xn(k+1) |
xn(k) |
xn−1(k) |
|
z−1 |
z−1 |
|
λn |
λn−1 |
|
cn,d |
c |
|
|
n−1,d |
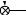
 z−1 x1(k)
z−1 x1(k)
λ1
c1,d


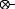
 y(k)
y(k)


 y(k )
y(k )
|
|
|
|
c1,s |
|
|
|
c2,s |
|
cn,s |
|
u(k) |
z−1 |
x1(k) |
|
z−1 |
x2(k) |
z−1 |
xn (k) |
|
|||
|
|
|
|
|
|
|
|
||||
an |
|
|
|
an−1 |
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(k ) |
|
|
|
|
b1 |
|
|
|
b1 |
|
bn |
|
u(k) |
z−1 xn (k) |
z−1 xn−1(k) |
z−1 x1 (k ) |
|
|||||||
|
|
|
|
a1 |
|
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
2 |
|
n |
|
u(k) |
|
|
|
|
|
|
|
|
|
|
|
bn,B |
|
|
|
|
b |
|
|
|
b |
|
|
|
|
|
|
|
n−1,B |
|
|
|
1,B |
|
|
|
|
z−1 |
xn(k) |
|
z−1 |
xn−1(k) |
z−1 |
x1(k) |
y(k) |
||
|
|
|
|
|
|
|
|||||
|
|
|
|
a1 |
|
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
2 |
|
n |
|
u(k) |
|
|
|
|
|
|
|
|
|
|
|
bn |
|
|
|
bn−1 |
|
|
|
b1 |
|
|
|
|
|
z−1 |
x1(k) |
z−1 |
x2(k) |
x (k) |
y(k ) |
||||
|
|
|
|
|
z−1 |
n |
|||||
an |
|
|
|
an−1 |
|
|
|
a1 |
|
|
|
Рис. 3.6. Структурные схемы, соответствующие каноническим формам описания в пространстве состояний
60

3.3.ПЕРЕХОДНЫЕ ПРОЦЕССЫ МОДЕЛЕЙ
ВПРОСТРАНСТВЕ СОСТОЯНИЙ
Рассмотрим поведение модели ДС в пространстве состояний при отсутствии входного воздействия (автономная система) x[k ] = 0, k ³ 0 , тогда в соответствии с (3.14) и (3.15)
z[k +1] = Ak z[0] = Az[k],
y[k ] = CAk z[0] = Cz[k].
Если для z[0] = z* при любых k ³ 0 имеет место тождество z[k ]= z* , то значение z = z* называют равновесным состоянием автономной ДС и будет выполняться z[k +1]= z[k ]= z* . Тогда
z* = Az*,
|
|
(I - A)z* = 0. |
(3.41) |
|
При условии, |
что det (I - A) ¹ 0 , следует, что единственным решени- |
|
ем |
(3.41) будет начало координат n-мерного |
пространства состояний, |
|
т.е. |
z* = 0 . А при |
det(I - A) = 0 существуют нетривиальные множества |
|
равновесных состояний, удовлетворяющие условию (3.41). В [10] показано, что ДС с равновесным состоянием асимптотически устойчива, и, следовательно, z[k] ® 0 при k ® ¥ , если выполняется условие
li < 1, i = 1, n,
где li – корни (полюсы) характеристического уравнения det(Il - A) = 0 .
|
|
li |
|
|
|
Для случая, когда |
|
= 0, i = 1, n , матрица A является нильпотент- |
|||
ной, и, следовательно, |
найдется такое число m [0, n] , что Am = 0 . Для |
||||
такой системы всегда выполнятся
z[n] = An z[0] = 0,
т.е. имеет место следующее положение.
Переходной процесс ДС n-го порядка с нулевыми значениями всех полюсов pi сходится из произвольного начального состояния z[0] к по-
ложению равновесия z* = 0 не более чем за n шагов.
61
Эти свойства автономных моделей ДС справедливы также для выходной переменной y[k ] = Cz[k] и для свободных составляющих пере-
ходных процессов zсв[k ]и yсв[k] возмущённых ДС.
Теперь рассмотрим поведение ДС при постоянном входном воздействии x[k ]= u = const , k ³ 0 . Для асимптотически устойчивой системы справедливо постоянное значение установившихся составляющих пере-
ходного процесса |
zуст [k ]= zуст = const , yуст[k ]= yуст = const , |
но тогда |
zуст [k + 1]= zуст [k ] |
и уравнение (3.14) примет вид |
|
|
zуст = Azуст + Bu. |
(3.42) |
Откуда |
zуст = (I - A)−1 Bu. |
|
|
|
Подставляя найденное решение в уравнение выхода (3.15), получим статическую характеристику рассматриваемой ДС
yуст = С(I - A)−1 Bu. |
(3.43) |
Учитывая выражение для передаточной характеристики ДС (3.17) формула (3.43) примет вид
yуст = W (1)u.
При условии, что det (I - A) ¹ 0 , алгебраическое уравнение (3.43) имеет единственное решение, а переходные процессы с течением времени k ® ¥ всегда сходятся к установившимся значениям zуст и yуст .
3.4. АНАЛИЗ СВОЙСТВ ДС В ПРОСТРАНСТВЕ СОСТОЯНИЙ
При решении задач управления методами пространства состояний предварительно рассматриваются некоторые свойства динамических систем, которые однозначно характеризуют возможности использования известной модели ДС для управления объектом. Такими свойствами явля-
ются достижимость, управляемость и наблюдаемость. Наличие этих свойств у объектов управления позволяет синтезировать управление с помощью простых математических операций.
3.4.1. Достижимость и управляемость |
|
Пусть ДС представлена моделью в пространстве состояний |
|
z[k +1] = Az[k ]+ Bx[k ], |
(3.44) |
y[k ] = Cz[k ], |
(3.45) |
62
где x[k ] – скалярное управляющее воздействие; y[k ] – скалярная выходная переменная, а также известны начальные условия z[0] = z0 . Проблема
исследования, таким образом, будет состоять в анализе параметров ДС, заданных в матрицах A, B, C .
Свойство достижимости определяется как существование такого конечного момента времени k f и такого ограниченного входного воздейст-
вия x[k ] [xmin , xmax ] , k [0, k f ] , которое переводит начальное состояние
системы z[0] = z0 в желаемое состояние z f . |
|
Состояние |
z[k ] линейной системы управляемо, если существует мо- |
мент времени k f |
и такой ограниченный входной сигнал x[k ] [xmin , xmax ] , |
k [0, k f ] , который переводит состояние системы z[0] ¹ 0 в состояние |
|
z[k f ]= 0 (начало координат), при условии, что время k f конечно.
Так как для непрерывных систем вида (3.44) каждое достижимое состояние управляемо, то при анализе непрерывных систем говорят только об управляемости, в то время как для ДС используют оба понятия. Сформируем необходимые критерии достижимости и управляемости ДС путём непосредственного нахождения дискретной входной последовательности x[k ] ,
необходимой для перевода системы из начального состояния в конечное. Для этого воспользуемся аналитическим решением уравнения (3.44) с помощью выражения (3.14)
k −1
z[k ]= Ak z[0]+ ∑Ak −i −1Bx[i].
i=0
Для исследования достижимости задаются начальные условия z[0] = z0 , тогда состояние ДС через количество шагов k , равного порядку
модели ДС k = n , будет определяться следующим образом:
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
z[n]= An z0 + ∑An−i −1Bx[i]= |
|
|
|
|
|
|
|
||||||
|
|
|
i = 0 |
|
|
|
|
|
|
|
|
|
|
= An z0 + An−1Bx[0]+ An−2 Bx[1]+ K+ Bx[n −1]= |
(3.46) |
||||||||||||
|
|
|
+ [B AB L |
|
|
B] |
x[n −1] |
|
|
|
|
||
= A |
n |
z0 |
A |
n −1 |
|
M |
|
= A |
n |
z0 |
+ U D x, |
||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x[0] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где U D = [B AB |
L An−1B] – |
матрица достижимости. |
|||||||||||
63
Выберем k f = n , z[n] = z f |
, тогда управляющая последовательность, |
|||||
согласно (3.46) будет равна |
|
|
|
|
|
|
x[n -1] |
|
(z f |
|
|
||
|
|
|
−1 |
n |
|
|
|
M |
|
= U D |
- A z0 ). |
(3.47) |
|
|
x[0] |
|
|
|
|
|
|
|
|
|
|
|
|
Это алгебраическое уравнение разрешимо тогда и только тогда, когда матрица достижимости UD обратима (невырождена), тогда можно найти n уравнений, решением которых является такой управляющий сигнал, что из начального состояния z0 система перейдет в желаемое конечное состояние z f , т.е. ранг матрицы достижимости равен n (рангом матрицы называется наибольший порядок её определителя, отличный от нуля):
rankU D = n. |
(3.48) |
Условия управляемости могут быть получены также из выражения |
|
(3.14) для начального условия z[0] = z0 ¹ 0 и конечного условия |
z f = 0 , |
если положить k f = n : |
|
−
0= An z0 + ∑An−i−1Bx[i]= An z0 +U D x,
i=0n 1
z0 = − A− nU D x = −UU x,
где матрица управляемости UU равна
UU = A− nU D = [A− n B |
A− n +1B L A−1B] . |
(3.49) |
|||
Тогда |
|
|
|
|
|
x[n -1] |
|
|
|
||
|
|
|
−1 |
z0. |
|
|
M |
|
= -UU |
(3.50) |
|
|
x[0] |
|
|
|
|
|
|
|
|
|
|
Сравнивая с выражением (3.47), можно заключить, что ДС будет управляемой только тогда, когда ранг матрицы управляемости равен по-
рядку модели ДС, т.е. |
|
rankUU = n. |
(3.51) |
64
Если матрица A не вырождена, условия достижимости и управляемости эквивалентны.
Рассмотрим два характерных случая:
а) B – матрица-столбец размером n ×1 . Матрицы UU и UD в этом случае – квадратные. Если определитель квадратной матрицы n ´n не равен нулю, то эта матрица имеет ранг, равный n ;
б) B – матрица размером n´m , что соответствует наличию m каналов управления. Матрицы управляемости и достижимости имеют n строк и n ×m столбцов, из которых можно составить n(m −1)+1 квадратных
матриц размерностью n ´n . Если хотя бы один из определителей этих матриц отличен от нуля, система будет полностью управляемой и ранг матрицы управляемости равен порядку системы n .
Вслучае, если ранг матриц достижимости или управляемости равен
ν< n , то ДС будет не полностью управляема, что соответствует наличию
νфазовых координат z1[k] , которые поддаются управлению, и n - n
фазовых координат z2[k] , которые не поддаются явному управлению.
С учётом этого исходную модель (3.44), (3.45) не полностью управляемой ДС можно представить в виде
z1[k + 1]= A z1[k ]+ A z2 [k ]+ Bx[k ], |
|
|||
11 |
12 |
[k ], |
|
|
z2 [k + 1]= A |
|
z2 |
(3.52) |
|
22 |
|
|
|
|
y[k ]= Cz[k ]. |
|
|
||
На рисунке 3.7 показан пример не полностью управляемой системы, описываемой выражением (3.52).
|
|
|
|
A11 |
|
|
|
|
|
|
|
|
z1[k +1] |
|
|
|
|
|
|
|
|
x[k] |
B |
Iz−1 |
|
z1[k ] |
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
C |
y[i] |
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A12 |
|
|
Iz−1 |
|
z2[k +1] |
|
|
|
|
|
z2[k] |
|
|
|
|
|||
|
|
|
|
A22 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.7. Пример не полностью управляемой системы
65

3.4.2. Наблюдаемость
Для осуществления управления необходимо иметь информацию о текущем состоянии системы, т.е. о значениях вектора состояния z[k ] в
каждый момент времени. Однако судить о состоянии системы можно только с помощью физических величин y[k ] , которые непосредственно
поддаются измерению, тогда как некоторые из переменных состояния являются абстрактными и не имеют физических аналогов в реальной системе. Таким образом, необходимо решить задачу определения вектора состояния по известному вектору входа и измеряемому вектору выхода.
Состояние z[k ] называется наблюдаемым, если в момент времени наблюдения k = 0 можно однозначно определить z[0] по данным измерения входных x[k ] и выходных y[k ] переменных на конечном интервале
времени.
Для выявления формальных условий наблюдаемости воспользуемся выражением (3.15), связывающим выходную переменную с начальным состоянием системы. Действие входного сигнала считается известным, поэтому общность решения не пострадает, если предположить, что систе-
ма автономна x[k ]= 0 , k = 0, n − 1 . Если известны значения выходной
переменной y[k ] на рассматриваемом интервале |
k = |
0, n −1 |
, то можно |
||
записать систему уравнений |
|
|
|
||
y[k ] = CA k z[0], k = |
|
|
(3.53) |
||
0, n −1. |
|||||
Или в развёрнутом виде |
|
|
|
||
y[0] = Cz[0], |
|
|
|
||
y[1] = CAz[0], |
|
|
|
||
M |
|
|
|
||
y[n −1] = CAn−1z[0]. |
|
|
|
||
Это уравнение можно записать в матричном виде
|
y[0] |
|
|
C |
|
|
|
y[1] |
|
|
CA |
|
(3.54) |
|
|
|
= |
|
z[0]. |
|
|
M |
|
|
M |
|
|
y[n −1] |
CAn−1 |
|
|
|||
|
|
|
|
|
|
|
Состояние z[0] можно получить из (3.54) только в том случае, если матрица наблюдаемости
66
|
|
|
|
C |
|
|
||
|
|
|
|
CA |
|
|
||
U |
|
= |
|
|
(3.55) |
|||
N |
|
M |
|
|||||
|
|
|
||||||
|
|
|
|
|
n−1 |
|
|
|
|
|
|
CA |
|
|
|
||
имеет ранг n . В том случае, если матрица наблюдаемости имеет ранг ν < n , то она будет являться не полностью наблюдаемой и, следователь-
но, будет иметь ν наблюдаемых переменных состояния z1[k] и n − ν не
наблюдаемых переменных z2[k] . Соответственно модель (3.44), (3.45) не полностью наблюдаемой ДС можно представить в виде
z1[k +1] = A z1[k ] |
+ B x[k ], |
|
|
z2 [k +1] = A |
11 |
1 |
|
z1[k ]+ A |
z2 [k ]+ B x[k ], |
(3.56) |
|
21 |
22 |
2 |
|
y[k ] = C z1[k ]. |
|
||
|
1 |
|
|
В общем случае система может содержать четыре группы фазовых координат:
–управляемую, но ненаблюдаемую часть z1[k] ;
–управляемую и наблюдаемую часть z2[k] ;
–неуправляемую и ненаблюдаемую часть z3[k] ;
–неуправляемую, но наблюдаемую часть z4[k] . Тогда модель для общего случая запишется в виде
z1[k + 1] = A z1[k ]+ A z2 [k ]+ A z3[k ]+ A z4 |
[k ]+ B x[k ], |
||||
11 |
12 |
13 |
|
14 |
1 |
z2 [k + 1]= A z1[k ]+ A z2 |
[k ]+ B x[k ], |
||||
|
21 |
22 |
|
2 |
|
|
z3[k + 1]= A33z3[k ]+ A34 z4 |
[k ], |
(3.57) |
||
|
z4 [k + 1]= A z4 [k ], |
|
|
||
|
y[k ] |
44 |
|
|
|
|
= C z1[k ]. |
|
|
|
|
|
|
1 |
|
|
|
На практике наблюдаемыми координатами обычно считаются те из них, которые могут быть непосредственно измерены датчиками различных типов. Даже если какая-либо фазовая координата и может быть вычислена по доступным для измерения выходным величинам, обработка измеренных величин будет, во-первых, сложной и, во-вторых, затруднена наличием помех.
67

4.ЗАДАЧИ АНАЛИЗА ДИСКРЕТНЫХ СИСТЕМ
4.1.АНАЛИЗ УСТОЙЧИВОСТИ ДИСКРЕТНЫХ СИСТЕМ
При анализе динамических систем управления первостепенной задачей является решение вопроса об их устойчивости. Именно это свойство характеризует свойство системы стабильно работать в нормальных режимах и при воздействии дестабилизирующих факторов. По сути, устойчивость отражает способность системы возвращаться в равновесное состояние, из которого она выводится внешними воздействиями. Устойчивость системы является обязательным техническим требованием, от которого напрямую зависят показатели качества и точности системы автоматического управления. Выражаясь иначе, можно заключить, что только устойчивая система является управляемой.
Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы. Говорят, что система устойчива «в малом», если определён факт наличия устойчивости, но не определены её границы. Система устойчива «в большом», когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы. Соответственно, и задача исследования систем на устойчивость может быть поставлена двояко:
1)устойчива ли система при заданном значении её параметров;
2)в каких диапазонах можно изменять параметры системы, не нарушая её устойчивости.
Вторая задача исследования имеет место при наладке и эксплуатации систем автоматического управления.
Система является устойчивой тогда и только тогда, когда реакция на ограниченное воздействие ограничена. Исходя из этого определения можно утверждать, что при воздействии на ДС дискретной дельтафункции δ(t) реакция системы должна быть ограничена и стремиться к
исходному состоянию с течением времени. Так как реакция ДС при воздействии на неё дискретной дельта-функции есть импульсная характеристика системы h(kTd ) , то
∞ |
|
|
|
|
|
|
∑ |
|
h(kTd ) |
|
< ∞. |
(4.1) |
|
|
|
|||||
k = |
0 |
|
|
|
|
|
Выражение (4.1) является необходимым и достаточным условием устойчивости по Ляпунову и сводится к требованию ограниченности суммы модуля импульсной характеристики ДС.
68
